Skip to main content
SpringerLink
Log in

Soret and Dufour effects in the flow of viscous fluid by a curved stretching surface

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

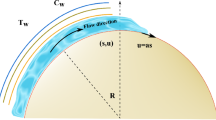
The main focus in this study is to study the flow of a viscous fluid through a curved stretched surface. Soret and Dufour effects along with Joule heating are incorporated. Appropriate transformations yield the nonlinear ordinary differential system. Convergent series solutions of velocity, temperature and concentration are constructed. Graphical illustrations thoroughly demonstrate the features of the involved pertinent parameters. Skin friction coefficient, Nusselt and Sherwood numbers are also obtained and discussed graphically. Current computations reveal that the radial velocity experience decline with the increase of Hartman number. Further, fluid temperature declines for higher Prandtl and Soret numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. R Ellahi, E Shivanian, S Abbasbandy, S U Rahman and T Hayat, Int. J. Heat Mass Transf. 55(23–24), 6384 (2012)

    Article  Google Scholar 

  2. E Sweet, K Vajravelu, R A V Gorder and I Pop, Commun. Nonlinear Sci. Numer. Simulat. 16(1), 266 (2011)

    Article  ADS  Google Scholar 

  3. Z Abbas, M Sheikh and I Pop, J. Taiwan Inst. Chem. Eng. 55, 69 (2015)

    Article  Google Scholar 

  4. M Turkyilmazoglu, Int. J. Non-Linear Mech. 44(4), 352 (2009)

    Article  ADS  Google Scholar 

  5. Y Lin and L Zheng, AIP Adv. 5, 107225 (2015)

    Article  ADS  Google Scholar 

  6. A Zeeshan, A Majeed and R Ellahi, J. Mol. Liq. 215, 549 (2016)

    Article  Google Scholar 

  7. M Kumari, I Pop and G Nath, Int. J. Non-Linear Mech. 45(5), 463 (2010)

    Article  ADS  Google Scholar 

  8. M Turkyilmazoglu, Chem. Eng. Sci. 84, 182 (2012)

    Article  Google Scholar 

  9. T Hayat, M Imtiaz and A Alsaedi, J. Mol. Liq. 212, 203 (2015)

    Article  Google Scholar 

  10. Y Lin, L Zheng, X Zhang, L Ma and G Chen, Int.J. Heat Mass Transf. 84, 903 (2015)

    Article  Google Scholar 

  11. M M Rashidi, M Nasiri, M Khezerloo and N Laraqi, J. Magn. Magn. Mater. 401, 159 (2016)

    Article  ADS  Google Scholar 

  12. M Sheikholeslami and H B Rokni, Int. J. Heat Mass Transf. 107, 288 (2017)

    Article  Google Scholar 

  13. L J Crane, J. Appl. Math. Phys. (ZAMP) 21, 645 (1970)

    Article  Google Scholar 

  14. R Cortell, J. King Saud University-Sci. 26, 161 (2013)

    Article  Google Scholar 

  15. F Mabood and K Das, Eur. Phys. J. Plus 131, 3 (2016)

    Article  Google Scholar 

  16. S M Ibrahim, P V Kumar and O D Makinde, Defect Diffus. Forum 387, 319 (2018)

    Article  Google Scholar 

  17. M Sajid, N Ali, T Javed and Z Abbas, Chin. Phys. Lett. 27(2), 024703 (2010)

    Article  ADS  Google Scholar 

  18. N C Rosca and I Pop, Eur. J. Mech. B/Fluids 51, 61 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  19. M Imtiaz, T Hayat and A Alsaedi, PLoS ONE 11(9), e0161641 (2016)

    Article  Google Scholar 

  20. M Imtiaz, T Hayat and A Alsaedi, Powder Technol. 310, 154 (2017)

    Article  Google Scholar 

  21. T Hayat, M Mustafa and I Pop, Commun. Nonlinear Sci. Numer. Simulat. 15(5), 1183 (2010)

    Article  ADS  Google Scholar 

  22. M Turkyilmazoglu and I Pop, Int. J. Heat Mass Transf. 55(25–26), 7635 (2012)

    Article  Google Scholar 

  23. C Y Cheng, Int. J. Commun. Heat Mass Transf. 39, 72 (2012)

    Article  Google Scholar 

  24. D Pal and H Mondal, J. Energy Convers. Manag. 62, 102 (2012)

    Article  Google Scholar 

  25. A A Altawallbeh, B S Bhadauria and I Hashim, Int. J. Heat Mass Transf. 59, 103 (2013)

    Article  Google Scholar 

  26. A F Al-Mudhaf, A M Rashad, S E Ahmed, A J Chamkha and S M M El-Kabeir, Int. J. Mech. Sci. 140, 172 (2018)

    Article  Google Scholar 

  27. S Abbasbandy and A Shirzadi, Commun. Nonlinear Sci. Numer. Simulat. 16(1), 112 (2011)

    Article  ADS  Google Scholar 

  28. R Ellahi, M Raza and K Vafai, Math. Comput. Model. 55(7–8), 1876 (2012)

    Article  Google Scholar 

  29. T Hayat, M Imtiaz, A Shafiq and A Alsaedi, J. Mol. Liq. 229, 501 (2017)

    Article  Google Scholar 

  30. M Pan, L Zheng, F Liu and X Zhang, J. Appl. Math. Model 40, 8974 (2016)

    Article  Google Scholar 

  31. J Sui, L Zheng and X Zhang, Int. J. Therm. Sci. 104, 461 (2016)

    Article  Google Scholar 

  32. T Hayat, M Kanwal, S Qayyum, I Khan and A Alsaedi, Pramana – J. Phys. 93(4): 54 (2019)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Social and Behavioral Sciences, National University of Medical Sciences, Rawalpindi, 46000, Pakistan

    Maria Imtiaz

  2. Department of Mathematics, Quaid-I-Azam University, Islamabad, 44000, Pakistan

    Hira Nazar & Tasawar Hayat

  3. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    Tasawar Hayat & Ahmed Alsaedi

Authors
  1. Maria Imtiaz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hira Nazar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tasawar Hayat
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ahmed Alsaedi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maria Imtiaz.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Imtiaz, M., Nazar, H., Hayat, T. et al. Soret and Dufour effects in the flow of viscous fluid by a curved stretching surface. Pramana - J Phys 94, 48 (2020). https://doi.org/10.1007/s12043-020-1922-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-020-1922-0

Keywords

PACS Nos

Search

Navigation