Abstract
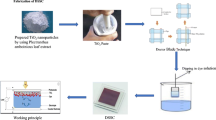
In the present work, dye-sensitised solar cell (DSSC) is fabricated using natural dye (Tecoma Stans)-sensitised \(\hbox {TiO}_{\mathrm {2\, }}\) as the photoanode, platinum as the counter electrode and lithium iodide and iodine as the electrolyte. Initially, \(\hbox {TiO}_{\mathrm {2\, }}\) nanoparticles are synthesised by the sol–gel technique using glacial acetic acid as the hydrolysing agent. The photoanodes are prepared by the Doctor Blade technique using the synthesised nanoparticles coated onto the fluorine-doped tin oxide (FTO) substrate and annealed at 400, 500 and \(600^{\circ }\hbox {C}\) for 30 min. Structural analysis shows the anatase phase of the \(\hbox {TiO}_{\mathrm {2}}\) thin film with a tetragonal crystal structure. The optical transmittance is found to be around 95% with an optical band gap close to 3.1 eV and increases with an increase in annealing temperature. From the PL emission spectra, the excitation of the titania band is observed. The pigment flavan-4-ol which acts as a sensitiser is extracted from Tecoma Stans flower. From the absorption study of the pigment, the active region of radiation and the band gap are found to be around 550 nm and 2 eV respectively. FTIR analysis of the pigment shows a stable structure similar to that of the prepared photoanodes. CV analysis of the sensitiser shows maximum oxidation within the active region. Field emission scanning electron microscope (FE-SEM) analysis shows that the prepared photoanode (\(600^{\circ }\hbox {C}\)) has spherical shape. The overall photoconversion efficiency of Tecoma Stans-sensitised \(\hbox {TiO}_{\mathrm {2}}\) photoanode is 0.4491%.









Similar content being viewed by others
References
Brian O’Regan and Michael Gratzel, Nature 335, 737 (1991)
Qifeng Zhang and Guozhong Cao, Nano Today 6, 91 (2011)
X Zhang, M Ge, J Dong, J Huang, J He and Y Lai, ACS Sustain. Chem. Eng. 7, 558 (2019)
Yu Bai, Ivan Mora-Sero, Filippo De Angelis, Juan Bisquert and Peng Wang, Chem. Rev. 114, 10095 (2014)
He, Chao Liu, Kevin D Dubois, Tong Jin, Michael E Louis and Gonghu Li, Ind. Eng. Chem. Res. 51, 11841 (2012)
Z Fei Yin, L Wu, H Gui Yang and Y Hua Su, Phys. Chem. Chem. Phys. 15, 4844 (2013)
X Chen and S S Mao, Chem. Rev. 107, 2891 (2007)
J Nisar, Z Topalian, A De Sarkar, L Osterlund and R Ahuja, ACS Appl. Mater. Interfaces 5, 8516 (2013)
Z Xiu, M H Alfaruqi, J Gim, J Song, S Kim, T V Thi, P Duong, V Mathew and J Kim, Chem. Commun. 51, 12274 (2015)
Y Duan, N Fu, Q Liu, Y Fang, X Zhou, J Zhang and Y Lin, J. Phys. Chem. C 116, 8888 (2012)
K M Aiswaraya, T Raguram and K S Rajni, Polyhedron 176, 114267 (2020)
S Kathirvel, C Su, H C Lin, B R Chen and W R Li, Mater. Lett. 129, 149 (2014)
T Raguram and K S Rajni, J. Sol-Gel Sci. Technol. 93, 202 (2020)
L M Sikhwivhilu, S S Ray and N J Coville, Appl. Phys. A 94, 963 (2008)
M Okuya, K Nakade and S Kaneka, Sol. Energy Mater. Sol. Cells 70, 425 (2002)
S Sato, A Sobczynski, J M White, A J Bard, A Campion, M A Fox, T E Mallouk and S E Webber, J. Photochem. Photobiol. A 50, 283 (1989)
G Anburaj, M Marimuthu, V Rajasudha and R Manikandan, J. Pharmacogn Phytochem. 5, 172 (2016)
R Azimirad and S Safa, Pramana – J. Phys. 86, 653 (2016)
C R Tubio, F Guirian, J R Salgueiro and A Gil, Mater. Lett. 141, 203 (2015)
V S Mohite, M A Mahadik, S S Kumbhar, V P Kothavale, A V Moholkar, K Y Rajpure and C Bhosale, Ceram. Int. 41, 2202 (2015)
T Raguram and K S Rajni, Appl. Phys. A 125, 288 (2019)
Moges Tsegaa and F B Dejene, Heliyon 3, e00246 (2017), https://doi.org/10.1016/j.heliyon.2017.e00246
L A Patterson, Phys. Rev. 56, 978 (1939)
Wenxiu Que, A Uddin and X Hu, J. Power Sources 159, 353 (2006)
Dan Tian, Chan-Juan Zhou and Ji-Huan He, Fractals 26, 1850083 (2018)
G E Fougere, J R Weertman, R W Siegel and S Kim, Scripta Metall. Mater. 26, 1879 (1992)
A Chokshi, A Rosen, J Karch and H Gleiter, Scripta Metall. 23, 1679 (1989)
Madan Singh and Mahipal Singh, Pramana – J. Phys. 84, 609 (2015)
V Swamy and L S Dubrovinsky, J. Phys. Chem. Solids 62, 673 (2001)
D R Hummer and P J Heaney, Powder Diffraction 22, 362 (2007)
A K M Muaz, U Hashim, Fatimah Ibrahim, K L Thong, Mas S Mohktar and Wei-Wen Liu, Microsyst. Tecchol. 22, 871 (2016)
R Nasiraei, M R Fadavieslam and H Azimi-juybari, Pramana – J. Phys. 87: 30 (2016)
N Gokilamani, N Muthukumarasamy and M Thambidurai, Adv. Mat. Res. 676, 108 (2013)
R S Dubey, Mater. Lett. 215, 312 (2018)
T H Gfroerer, Photoluminescence in analysis of surface and interfaces, Encyclopedia of analytical chemistry edited by R A Meyers (John Wiley & Sons Ltd, Chichester, 2000)
M Zacharias and P M Fauchet, Appl. Phys. Lett. 71, 380 (1997)
Yin Zhao, Chunzhong Li, Xiuhong Liu, Feng Gu, Haibo Jiang, Wei Shao, Ling Zhang and Ying He, Mater. Lett. 61, 79 (2007)
F Leiter, H Alves, D Pfisterer, N G Romanov, D M Hofmann and B K Meyer, Physica B 201, 340 (2003)
D Pan, N Zhao, Q Wang, S Jiang, X Ji and L An, Adv. Mater. 17, 1991 (2005)
Mou Pal, Umapada Pal, Justo Miguel, Gracia Y Jimenez and Felipe Perez-Rodriguez, Nanoscale Res. Lett. 7, 1 (2012)
W F Zhang, M S Zhang and Z Yin, Phy. Status Solidi A 179, 319 (2000)
Isao Nakamura, Nobuaki Negishi, Shuzo Kutsuna, Tatsuhiko Ihara, Shinichi Sugihara and Koji Takeuchi, J. Mol. Catal. 161, 205 (2000)
T S Senthil, N Muthukumarasamy, S Agilan, M Thambidurai and R Balasundaraprabhu, Mater. Sci. Eng. B 174, 102 (2010)
Y H Chang, C M Liu, C Chen and H E Cheng, J. Electrochem. Soc. 159, D401 (2012)
B Choudhury and A Choudhury, Physica E 56, 364 (2014)
Michael R Hoffman, Scot T Martin, Wonyong Choi and Detlef W Bahnemann, Chem. Rev. 95, 69 (1995)
Wei Kong, Bo Liu, Bo Ye, Zhongping Yu, Hua Wang, Guodong Qian and Zhiyu Wang, J. Nanomater. 2011, Article ID 467083 (2011)
M S El Naschie, Chaos Solitons Fractals 30, 579 (2006)
Ji-Huan He, Yu-Qin Wan and Lan Xu, Chaos Solitons Fractals 33, 26 (2007)
Ya Li and Ji-Huan He, Adsorpt. Sci. Technol. 37, 425 (2019), https://doi.org/10.1177/0263617419828268
G Oskam, B V Bergeron and G J Meyer, J. Phys. Chem. B 105, 6867 (2001)
H Zhou, L Wu, Y Gao and T Ma, J. Photochem. Photobiol. A 219, 188 (2011)
T Raguram and K S Rajni, Optik 204, 164169 (2020)
N Gokilamani, N Muthukumarasamy, M Thambidurai, A Ranjitha, D Velauthapillai, T S Senthil and R Balasundaraprabhu, J. Mater. Sci.: Mater. Electron. 24, 3394 (2013)
Acknowledgements
The authors would like to thank Dr K Murugadass, Assistant Professor, Department of Sciences, Dr M Karthega, Assistant Professor, Amrita Materials Science Lab, Dr T G Sathish Babu, Associate Professor, Bio-Sensor Research Lab and Dr Sudip Kumar Batabyal, Research Scientist, Centre for Industrial Research and Innovation (ACIRI), Amrita Vishwa Vidyapeetham, Coimbatore, India, for providing lab facilities and their constant support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vedavarshni, S., Raguram, T. & Rajni, K.S. Studies on the characteristics of \(\hbox {TiO}_2\) photoanode and flavanol pigment as a sensitiser for DSSC applications. Pramana - J Phys 94, 112 (2020). https://doi.org/10.1007/s12043-020-01982-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12043-020-01982-1