Skip to main content
SpringerLink
Log in

Travelling wave solutions of (2\(+\)1)-dimensional generalised time-fractional Hirota equation

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

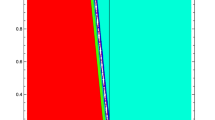
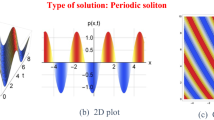
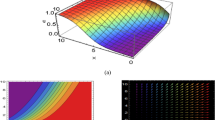
In this article, we have developed new exact analytical solutions of a nonlinear evolution equation that appear in mathematical physics, a \((2+1)\)-dimensional generalised time-fractional Hirota equation, which describes the wave propagation in an erbium-doped nonlinear fibre with higher-order dispersion. By virtue of the tanh-expansion and complete discrimination system by means of fractional complex transform, travelling wave solutions are derived. Wave interaction for the wave propagation strength and angle of field quantity under the long wave limit are analysed: Bell-shape solitons are found and it is found that the complex transform coefficient in the system affects the direction of the wave propagation, patterns of the soliton interaction, distance and direction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. R Hirota, J. Math. Phys. 14, 805 (1973)

    Article  ADS  Google Scholar 

  2. M Eslami, Optik 126(23), 3987 (2016)

    Article  ADS  Google Scholar 

  3. M Eslami, Optik 126(13), 1312 (2015)

    Article  ADS  Google Scholar 

  4. M Eslami, Nonlinear Dyn. 85(2), 813 (2016)

    Article  MathSciNet  Google Scholar 

  5. M Eslami and M Mirzazadeh, Nonlinear Dyn. 83(1–2), 731 (2016)

    Article  Google Scholar 

  6. M Eslami, A Neyrame and M Ebrahimi, J. King Saud Univ. Sci. 24(1), 69 (2012)

    Article  Google Scholar 

  7. M Eslami and M Mirzazadeh, Rep. Math. Phys. 73(1), 77 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  8. A Neirameh and M Eslami, Scientia Iranica 24(2), 715 (2017)

    Article  Google Scholar 

  9. M Ekici, M Mirzazadeh and M Eslami, Nonlinear Dyn. 84(2), 669 (2016)

    Article  Google Scholar 

  10. M Mirzazadeh, M Eslami and A H Arnous, Eur. Phys. J. Plus 130(1), 1 (2015)

    Article  Google Scholar 

  11. A Biswas, M Mirzazadeh, M Eslami, D Milovic and M Belic, Frequenz 68(11–12), 525 (2014)

    ADS  Google Scholar 

  12. M Eslami and M Mirzazadeh, Ocean Engng 83, 133 (2014)

    Article  Google Scholar 

  13. M Eslami and A Neirameh, Eur. Phys. J. Plus 129(4), 54 (2014)

    Article  Google Scholar 

  14. M Mirzazadeh, M Eslami and A Biswas, Comput. Appl. Math. 33(3), 831 (2014)

    Article  MathSciNet  Google Scholar 

  15. M Eslami, M A Mirzazadeh and A Neirameh, Pramana – J. Phys. 84, 3 (2015)

    Article  ADS  Google Scholar 

  16. K A Gepreel, T A Nofal and N S Al-Sayali, IAENG Eng. Lett. 24, 274 (2016)

    Google Scholar 

  17. X Huang, Phys. Lett. A 380, 2136 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  18. T Jia, Y Chai and H Hao, Superlatt. Microstruc. 105, 172 (2017)

    Article  ADS  Google Scholar 

  19. S T Demiray, Y Pandir and H Bulut, Optik 127, 1848 (2016)

    Article  ADS  Google Scholar 

  20. Y Wu, X Geng, X Hu and S Zhu, Phys. Lett. A 255, 259 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  21. X Xin, Y Liu and X Liu, Appl. Math. Lett. 55, 63 (2016)

    Article  MathSciNet  Google Scholar 

  22. J I Kanel and M Kirane, Commun. Appl. Anal. 4, 385 (2000)

    MathSciNet  Google Scholar 

  23. J H He, Comput. Meth. Appl. Mech. Engng 167, 57 (1998)

    Article  ADS  Google Scholar 

  24. J H He, Bull. Sci. Tech. Soc. 15, 86 (1999)

    MathSciNet  Google Scholar 

  25. R Gorenflo, F Mainardi, E Scalas and M Raberto, Mathematical finance (Konstanz, 2000), Trends Math. 171 (2001)

  26. R Hilfer, Applications of fractional calculus in physics (World Scientific, Singapore, 2000)

    Book  MATH  Google Scholar 

  27. R Metzler and J Klafter, J. Phys. A 37, R161 (2004)

    Article  ADS  Google Scholar 

  28. Y A Rossikhin and M V Shitikova, Acta Mech. 120, 109 (1997)

    Article  MathSciNet  Google Scholar 

  29. M Kirane and S A Malik, Nonlinear Anal. 73, 3723 (2010)

    Article  MathSciNet  Google Scholar 

  30. T Bakkyaraj and R Sahadevan, Nonlinear Dyn. 77, 1309 (2014)

    Article  Google Scholar 

  31. L Cui, L Yan and Y Liu, Thermal. Sci. 19, 1173 (2015)

    Article  Google Scholar 

  32. Z Z Ganji, D D Ganji and Y Rostamiyan, Appl. Math. Model. 33, 3107 (2009)

    Article  MathSciNet  Google Scholar 

  33. M Merdan, Proc. Rom. Acad. Ser. A: Math. Phys. Tech. Sci. Inf. Sci. 16, 3 (2015)

    MathSciNet  Google Scholar 

  34. M Merdan, A Gökdogan, A Yildirim and S Mohyud-Din, Int. J. Numer. Methods Heat Fluid Flow 23, 927 (2013)

    Article  Google Scholar 

  35. M Mirzazadeh, Pramana – J. Phys. 85, 17 (2015)

    Article  ADS  Google Scholar 

  36. M Eslami, B F Vajargah, M Mirzazadeh and A Biswas, Indian J. Phys. 88(2), 177 (2014)

    Article  ADS  Google Scholar 

  37. M Ekici, M Mirzazadeh, M Eslami, Q Zhou and S P Moshokoa, Optik 127(22), 10659 (2016)

    Article  ADS  Google Scholar 

  38. N Taghizadeh, M Mirzazadeh, M Rahimian and M Akbari, Ain Shams Engng J. 4(4), 897 (2013)

    Article  Google Scholar 

  39. M Mirzazadeh, M Eslami and A Biswas, Pramana – J. Phys. 82(3), 465 (2014)

    Article  ADS  Google Scholar 

  40. A A Kilbas, H M Srivastava and J J Trujillo, Theory and applications of fractional differential equations, North-Holland Mathematics Studies (Elsevier, Amsterdam, The Netherlands, 2006) Vol. 204

  41. T Odzijewicz, A B Malinowska and D F M Torres, Nonlinear Anal. 75, 1507 (2012)

    Article  MathSciNet  Google Scholar 

  42. I Podlubny, Fractional differential equations (Academic Press, San Diego, 1999)

    MATH  Google Scholar 

  43. E G Fan, Phys. Lett. A 277, 212 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  44. A M Wazwaz, Chaos Solitons Fractals 25, 55 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  45. J H He, S K Elagan and Z B Li, Phys. Lett. A 376, 257 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  46. Z B Li and J H He, Math. Comput. Appl. 15, 97 (2011)

    Google Scholar 

  47. W H Su, X J Yang, H Jafari and D Baleanu, Adv. Differ. Equ. 2013, 97 (2013)

    Article  Google Scholar 

  48. E M Zayed, Y A Amer and R M Shohib, J. Assoc. Arab Univ. Basic Appl. Sci. 19, 59 (2016)

    Google Scholar 

  49. C S Liu, Comput. Phys. Commun. 181, 317 (2010)

    Article  ADS  Google Scholar 

  50. C S Liu, Phys. arXiv:nlin/0609058

  51. L Yang and Z B Ceng, Sci. China Ser. E 39, 628 (1996)

    MathSciNet  Google Scholar 

  52. K A Gepreel, Adv. Differ. Equ. 2014, 286 (2014)

    Article  Google Scholar 

  53. A Z Fino and M Kirane, Quart. Appl. Math. 70, 133 (2012)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Hexi University, Beihuan Road, 846, Zhangye, 734000, China

    Youwei Zhang

Authors
  1. Youwei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Youwei Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y. Travelling wave solutions of (2\(+\)1)-dimensional generalised time-fractional Hirota equation. Pramana - J Phys 90, 34 (2018). https://doi.org/10.1007/s12043-018-1522-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-018-1522-4

Keywords

PACS Nos

Search

Navigation