Skip to main content
SpringerLink
Log in

Topological Disk Mesh Morphing Based on Area-Preserving Parameterization

  • Computer Science
  • Published:
Wuhan University Journal of Natural Sciences

Abstract

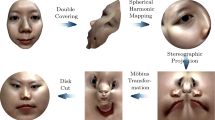
Mesh morphing is a technique which gradually deforms a mesh into another one. Mesh parameterization, a powerful tool adopted to establish the one-to-one correspondence map between different meshes, is of great importance in 3D mesh morphing. However, current parameterization methods used in mesh morphing induce large area distortion, resulting in geometric information loss. In this paper, we propose a new morphing approach for topological disk meshes based on area-preserving parameterization. Conformal mapping and Möbius transformation are computed firstly as rough alignment. Then area preserving parameterization is computed via the discrete optimal mass transport map. Features are exactly aligned through radial basis functions. A surface remeshing scheme via Delaunay refinement algorithm is developed to create a new mesh connectivity. Experimental results demonstrate that the proposed method performs well and generates high-quality morphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alexa M. Recent advances in mesh morphing[J]. Computer Graphics Forum, 2002, 21(2): 173–198.

    Article  Google Scholar 

  2. Zhang L, Liu L, Ji Z, et al. Manifold Parameterization[M]. Berlin: Springer-Verlag, 2006: 160–171.

    Google Scholar 

  3. Yeh I, Lin C, Sorkine O, et al. Template-based 3d model fitting using dual-domain relaxation[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(8): 1178–1190.

    Article  PubMed  Google Scholar 

  4. Wu H, Pan C, Zha H, et al. Partwise cross-parameterization via nonregular convex hull domains[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(10): 1531–1544.

    Article  PubMed  Google Scholar 

  5. Sumner R W, Popovic C J. Deformation transfer for triangle meshes[J]. ACM Transactions on Graphics (TOG), 2004, 23(3): 399–405.

    Article  Google Scholar 

  6. Kanai T, Suzuki H, Kimura F. Three-dimensional geometric metamorphosis based on harmonic maps[J]. The Visual Computer, 1998, 14(4): 166–176.

    Article  Google Scholar 

  7. Lee A W, Sweldens W, Schröder P, et al. MAPS: Multiresolution adaptive parameterization of surfaces[C] //Pro of the 25th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1998: 95–104.

    Google Scholar 

  8. Lin C, Lee T. Metamorphosis of 3d polyhedral models using progressive connectivity transformations[J]. IEEE Transactions on Visualization and Computer Graphics, 2005, 11(1): 2–12.

    Article  PubMed  Google Scholar 

  9. Lin C, Lee T, Chu H, et al. Progressive mesh metamorphosis[ J]. Computer Animation and Virtual Worlds, 2005, 16(3-4): 487–498.

    Article  Google Scholar 

  10. Mocanu B, Zaharia T. A complete framework for 3D mesh morphing[C] //Proceedings of the 11th ACM SIGGRAPH International Conference on Virtual-Reality Continuum and Its Applications in Industry. New York: ACM Press, 2012: 161–170.

    Google Scholar 

  11. Peng C, Timalsena S. Fast mapping and morphing for genus-zero meshes with cross spherical parameterization[J]. Computers and Graphics, 2016, 59: 107–118.

    Article  Google Scholar 

  12. Gregory A, State A, Lin M C, et al. Interactive surface decomposition for polyhedral morphing[J]. The Visual Computer, 1999, 15(9): 453–470.

    Article  Google Scholar 

  13. Kraevoy V, Sheffer A. Cross-parameterization and compatible remeshing of 3D models[J]. ACM Transactions on Graphics (TOG), 2004, 23(3): 861–869.

    Article  Google Scholar 

  14. Garner C, Jin M, Gu X, et al. Topology-driven surface mappings with robust feature alignment[C] //Vis 05 IEEE Visualization. Washington D C: IEEE, 2005: 543–550.

    Google Scholar 

  15. Litke N, Droske M, Rumpf M, et al. An image processing approach to surface matching[C] //Symposium on Geometry Processing. Washington D C: IEEE, 2005: 207–216.

    Google Scholar 

  16. Yueh M, Gu X D, Lin W, et al. Conformal surface morphing with applications on facial expressions[J/OL]. CoRR, arXivpreprint arXiv:1504.00097. 2015. http://dblp.org/rec/bib/journals/corr/YuehGLWY15.

    Google Scholar 

  17. Sheffer A, Praun E, Rose K, et al. Mesh parameterization methods and their applications[J]. Foundations and Trends in Computer Graphics and Vision, 2007, 2(2): 105–171.

    Article  Google Scholar 

  18. Praun E, Hoppe H. Spherical parametrization and remeshing[ J]. ACM Transactions on Graphics (TOG), 2003, 22(3): 340–349.

    Article  Google Scholar 

  19. Mocanu B, Zaharia T. Direct spherical parameterization of 3D triangular meshes using local flattening operations [C]// Advances in Visual Computing. Berlin: Springer-Verlag, 2011: 607–618.

    Chapter  Google Scholar 

  20. Hu K, Yan D, Bommes D, et al. Error-bounded and feature preserving surface remeshing with minimal angle improvement [J]. IEEE Transactions on Visualization and Computer Graphics, 2017, 23(12):2560–2573.

    Article  PubMed  Google Scholar 

  21. Yang Y L, Guo R, Luo F, et al. Generalized discrete Ricci flow[J]. Computer Graphics Forum, 2009, 28(7): 2005–2014.

    Article  Google Scholar 

  22. Zou G, Hu J, Gu X, et al. Authalic parameterization of general surfaces using lie advection [J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(12): 2005–2014.

    Article  PubMed  Google Scholar 

  23. Yoshizawa S, Belyaev A, Seidel H P. A fast and simple stretch-minimizing mesh parameterization [C] //Shape Modeling Applications Proceedings. Washington D C: IEEE, 2004: 200–208.

    Google Scholar 

  24. Monge G. M'emoire sur la th'eorie des d'eblais et des remblais[J]. Histoire de l′Acad′emie Royale des Sciences de Paris, avec les M′emoires de Math′ematiqueet de Physique pour la meme ann′ee, 1781: 666–704.

    Google Scholar 

  25. Kantorovich L V E. On a problem of Monge[J]. Uspekhi Mat Nauk, 1948, 3: 225–226.

    Google Scholar 

  26. Brenier Y. Polar factorization and monotone rearrangement of vector-valued functions[J]. Communications on Pure & Applied Mathematics, 1991, 44(4): 375–417.

    Article  Google Scholar 

  27. Alexadrov A D. Convex Polyhedral [M]. Berlin: Springer-Verlag, 2005.

    Google Scholar 

  28. Aurenhammer F. Power diagrams: Properties, algorithms and applications[J]. Siam Journal on Computing, 1987, 16(1): 78–96.

    Article  Google Scholar 

  29. Gu X, Luo F, Sun J, et al. Variational principles for Minkowski type problems, discrete optimal transport, and discrete Monge-Ampere equations[J]. Asian Journal of Mathematics, 2016, 20(2): 383–398.

    Article  Google Scholar 

  30. Su K, Cui L, Qian K, et al. Area-preserving mesh parameterization for poly-annulus surfaces based on optimal mass transportation[J]. Computer Aided Geometric Design, 2016, 46: 76–91.

    Article  Google Scholar 

  31. Sieger D, Menzel S, Botsch M. RBF morphing techniques for simulation-based design optimization[J]. Engineering with Computers, 2014, 30(2): 161–174.

    Article  Google Scholar 

  32. Shewchuk J R. Delaunay refinement algorithms for triangular mesh generation[J]. Computational Geometry, 2002, 22(1): 21–74.

    Article  Google Scholar 

  33. Solomon J, De Goes F, Peyre G, et al. Convolutional Wasserstein distances: Efficient optimal transportation on geometric domains[J]. ACM Transactions on Graphics (TOG), 2015, 34(4): 66.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer, Wuhan University, Wuhan, Hubei, 430072, China

    Cailing Chen & Kehua Su

  2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan, Hubei, 430072, China

    Xinyan Zhu

Authors
  1. Cailing Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kehua Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xinyan Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kehua Su.

Additional information

Foundation item: Supported by the National Natural Science Foundation of China (61772379), and the National Key Research and Development Program of China (2016YFB052204)

Biography: CHEN Cailing, female, Master candidate, research direction: computational conformal geometry.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, C., Su, K. & Zhu, X. Topological Disk Mesh Morphing Based on Area-Preserving Parameterization. Wuhan Univ. J. Nat. Sci. 23, 201–209 (2018). https://doi.org/10.1007/s11859-018-1311-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11859-018-1311-4

Key words

CLC number

Search

Navigation