Skip to main content

Advertisement

SpringerLink
Log in

A Comparative Study of Metaheuristic Algorithms for Reliability-Based Design Optimization Problems

  • Original Paper
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

Abstract

The ever-increasing demands for resource-saving, engineering technology progress, and environmental protection stimulate the progress of the progressive design method. As an excellent promising design method for dealing with the inevitable uncertainty factors, reliability-based design optimization (RBDO) is capable of offering reliable and robust results and minimizing the cost under the prescribed uncertainty level, which can provide a trade-off between economy and safety. However, the primary challenges, including global convergence capacity and complicated mixed design variable type, hinder the wider application of RBDO. This study presents a comprehensive work on the application of ten popular and recent metaheuristic algorithms of five engineering problems. Furthermore, we focus on the RBDO equip with metaheuristic algorithms about its global convergence, robustness, accuracy, and computational speed. This paper also presents the major difference of convergence property between metaheuristic algorithms and gradient algorithms. The detailed statement of this study presents the state-of-the-art in RBDO to demonstrate its crucial technologies and great challenges, as well as the beneficial future development direction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Georgioudakis M, Lagaros ND, Papadrakakis M (2017) Probabilistic shape design optimization of structural components under fatigue. Comput Struct 182(4):252–266

    Google Scholar 

  2. Jiang C, Qiu HB, Gao L, Cai XW, Li PG (2017) An adaptive hybrid single-loop method for reliability-based design optimization using iterative control strategy. Struct Multidiscip Optim 56(6):1271–1286

    MathSciNet  Google Scholar 

  3. Youn BD, Choi KK, Yang RJ, Gu L (2004) Reliability-based design optimization for crashworthiness of vehicle side impact. Struct Multidiscip Optim 26(3–4):272–283

    Google Scholar 

  4. Meng Z, Zhang Z, Zhou H (2020) A novel experimental data-driven exponential convex model for reliability assessment with uncertain-but-bounded parameters. Appl Math Model 77(1):773–787

    MathSciNet  MATH  Google Scholar 

  5. Wang L, Liu D, Yang Y, Hu J (2019) Novel methodology of non-probabilistic reliability-based topology optimization (NRBTO) for multi-material layout design via interval and convex mixed uncertainties. Comput Methods Appl Mech Eng 346(4):550–573

    MathSciNet  MATH  Google Scholar 

  6. Del Rosario Z, Fenrich RW, Iaccarino G (2019) Cutting the double loop: theory and algorithms for reliability-based design optimization with parametric uncertainty. Int J Numer Methods Eng 118(12):718–740

    MathSciNet  Google Scholar 

  7. Elishakoff I, Haftka R, Fang J (1994) Structural design under bounded uncertainty optimization with anti-optimization. Comput Struct 53(6):1401–1405

    MATH  Google Scholar 

  8. Deb K, Gupta S, Daum D, Branke J, Mall AK, Padmanabhan D (2009) Reliability-based optimization using evolutionary algorithms. IEEE Trans Evol Comput 13(5):1054–1074

    Google Scholar 

  9. Chen CT, Chen MH, Horng WT (2014) A cell evolution method for reliability-based design optimization. Appl Soft Comput 15(2):67–79

    Google Scholar 

  10. Valdebenito MA, Schueller GI (2010) Reliability-based optimization considering design variables of discrete size. Eng Struct 32(9):2919–2930

    Google Scholar 

  11. Huang HZ, Zhang X (2009) Design optimization with discrete and continuous variables of aleatory and epistemic uncertainties. J Mech Des 131(3):031006–031013

    Google Scholar 

  12. Yang IT, Hsieh YH (2011) Reliability-based design optimization with discrete search space. In: IEEE international conference on quality and reliability, pp 90–94

  13. Yao W, Chen X, Luo W, Van Tooren M, Guo J (2011) Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Prog Aerosp Sci 47(6):450–479

    Google Scholar 

  14. Chen Z, Qiu H, Gao L, Li P (2013) An optimal shifting vector approach for efficient probabilistic design. Struct Multidiscip Optim 47(6):905–920

    Google Scholar 

  15. Nikolaidis E, Burdisso R (1988) Reliability-based optimization: a safety index approach. Comput Struct 28(6):781–788

    MATH  Google Scholar 

  16. Ting Lin P, Chang Gea H, Jaluria Y (2011) A modified reliability index approach for reliability-based design optimization. J Mech Des 133(4):044501–044507

    Google Scholar 

  17. Jiang C, Han S, Ji M, Han X (2015) A new method to solve the structural reliability index based on homotopy analysis. Acta Mech 226(4):1067–1083

    MathSciNet  Google Scholar 

  18. Byeng Y, Kyung C, Liu D (2004) Enriched performance measure approach (PMA+) for reliability-based design optimization. In: 10th AIAA/ISSMO multidisciplinary analysis and optimization conference American institute of aeronautics and astronautics, pp 2004–01–1284

  19. Tu J, Choi KK, Park YH (1999) A new study on reliability-based design optimization. J Mech Des 121(4):557–564

    Google Scholar 

  20. Youn BD, Choi KK (2003) An investigation of nonlinearity of reliability-based design optimization approaches. J Mech Des 126(3):403–411

    Google Scholar 

  21. Jeong SB, Park GJ (2017) Single loop single vector approach using the conjugate gradient in reliability based design optimization. Struct Multidiscip Optim 55(4):1329–1344

    MathSciNet  Google Scholar 

  22. Liang J, Mourelatos ZP, Nikolaidis E (2007) A single-loop approach for system reliability-based design optimization. J Mech Des 129(12):1215–1224

    Google Scholar 

  23. Lim J, Lee B (2016) A semi-single-loop method using approximation of most probable point for reliability-based design optimization. Struct Multidiscip Optim 53(4):745–757

    MathSciNet  Google Scholar 

  24. Valdebenito M, Schuëller G (2010) A survey on approaches for reliability-based optimization. Struct Multidiscip Optim 42(5):645–663

    MathSciNet  MATH  Google Scholar 

  25. Meng Z, Yang D, Zhou H, Wang BP (2018) Convergence control of single loop approach for reliability-based design optimization. Struct Multidiscip Optim 57(3):1079–1091

    MathSciNet  Google Scholar 

  26. Keshtegar B, Hao P (2018) Enhanced single-loop method for efficient reliability-based design optimization with complex constraints. Struct Multidiscip Optim 57(4):1731–1747

    MathSciNet  Google Scholar 

  27. Du X, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233

    Google Scholar 

  28. Torii AJ, Lopez RH, Miguel LF (2016) A general RBDO decoupling approach for different reliability analysis methods. Struct Multidiscip Optim 54(2):317–332

    MathSciNet  Google Scholar 

  29. Aoues Y, Chateauneuf A (2010) Benchmark study of numerical methods for reliability-based design optimization. Struct Multidiscip Optim 41(2):277–294

    MathSciNet  MATH  Google Scholar 

  30. Hao P, Wang Y, Liu X, Wang B, Li G, Wang L (2017) An efficient adaptive-loop method for non-probabilistic reliability-based design optimization. Comput Methods Appl Mech Eng 324(9):689–711

    MathSciNet  MATH  Google Scholar 

  31. Zhou M, Luo Z, Yi P, Cheng G (2018) A two-phase approach based on sequential approximation for reliability-based design optimization. Struct Multidiscip Optim 57(2):489–508

    MathSciNet  Google Scholar 

  32. Yang XS (2009) Firefly algorithms for multimodal optimization. Stoch Algorithms Found Appl 5792(3):169–178

    MathSciNet  MATH  Google Scholar 

  33. Yildiz AR, Abderazek H (2019) A comparative study of recent non-traditional methods for mechanical design optimization. Arch Comput Methods Eng. https://doi.org/10.1007/s11831-019-09346-8

    Article  Google Scholar 

  34. Deb K, Padmanabhan D, Gupta S, Mall AK (2006) Handling uncertainties through reliability-based optimization using evolutionary algorithms. KanGAL report 2006009

  35. Salazar D, Rocco CM, Galvan BJ (2006) Optimization of constrained multiple-objective reliability problems using evolutionary algorithms. Reliab Eng Syst Saf 91(9):1057–1070

    Google Scholar 

  36. Sahoo L, Bhunia AK, Kapur PK (2012) Genetic algorithm based multi-objective reliability optimization in interval environment. Comput Ind Eng 62(1):152–160

    Google Scholar 

  37. Yang I, Hsieh YH (2011) Reliability-based design optimization with discrete design variables and non-smooth performance functions: AB-PSO algorithm. Autom Constr 20(5):610–619

    Google Scholar 

  38. Safaeian Hamzehkolaei N, Miri M, Rashki M (2016) An enhanced simulation-based design method coupled with meta-heuristic search algorithm for accurate reliability-based design optimization. Eng Comput 32(3):477–495

    MATH  Google Scholar 

  39. Chakri A, Yang XS, Khelif R, Benouaret M (2018) Reliability-based design optimization using the directional bat algorithm. Neural Comput Appl 30(8):2381–2402

    Google Scholar 

  40. Lobato FS, da Silva MA, Cavalini AA Jr, Steffen V Jr (2019) Reliability-based robust multi-objective optimization applied to engineering system design. Eng Optim. https://doi.org/10.1080/0305215x.2019.1577413

    Article  Google Scholar 

  41. Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor

    Google Scholar 

  42. Brest J, Greiner S, Boskovic B, Mernik M, Zumer V (2006) Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Trans Evol Comput 10(6):646–657

    Google Scholar 

  43. Koza JR (1992) Genetic programming: on the programming of computers by means of natural selection. MIT Press, Cambridge

    MATH  Google Scholar 

  44. Knowles JD, Corne DW (2000) Approximating the nondominated front using the Pareto archived evolution strategy. Evol Comput 8(2):149–172

    Google Scholar 

  45. Simon D (2008) Biogeography-based optimization. IEEE Trans Evol Comput 12(6):702–713

    Google Scholar 

  46. Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220(4598):671–680

    MathSciNet  MATH  Google Scholar 

  47. Erol OK, Eksin I (2006) A new optimization method: big bang–big crunch. Adv Eng Softw 37(2):106–111

    Google Scholar 

  48. Du H, Wu X, Zhuang J (2006) Small-world optimization algorithm for function optimization. In: International conference on advances in natural computation, pp 264–273

  49. Latas B (2011) Artificial chemical reaction optimization algorithm for global optimization. Expert Syst Appl 38(10):13170–13180

    Google Scholar 

  50. Formato RA (2009) Central force optimisation: a new gradient-like metaheuristic for multidimensional search and optimisation. Int J Bio Inspir Comput 1(4):217–238

    Google Scholar 

  51. Rashedi E, Nezamabadi Pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179(13):2232–2248

    MATH  Google Scholar 

  52. Kaveh A, Talatahari S (2010) A novel heuristic optimization method: charged system search. Acta Mech 213(3–4):267–289

    MATH  Google Scholar 

  53. Shah Hosseini H (2011) Principal components analysis by the galaxy-based search algorithm: a novel metaheuristic for continuous optimisation. Int J Comput Sci Eng 6(1–2):132–140

    Google Scholar 

  54. Kaveh A, Khayatazad M (2012) A new meta-heuristic method: ray optimization. Comput Struct 112(12):283–294

    Google Scholar 

  55. Kaveh A, Mahdavi V (2014) Colliding bodies optimization: a novel meta-heuristic method. Comput Struct 139(7):18–27

    Google Scholar 

  56. Hatamlou A (2013) Black hole: a new heuristic optimization approach for data clustering. Inf Sci 222(2):175–184

    MathSciNet  Google Scholar 

  57. Moghaddam FF, Moghaddam RF, Cheriet M (2012) Curved space optimization: a random search based on general relativity theory. arXiv preprint arXiv:1208.2214

  58. Eberhart R, Kennedy J (1995) A new optimizer using particle swarm theory. In: Proceedings of the sixth international symposium on micro machine and human science. IEEE, pp 39–43

  59. Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J Global Optim 39(3):459–471

    MathSciNet  MATH  Google Scholar 

  60. Das S, Biswas A, Dasgupta S, Abraham A, Bacterial foraging optimization algorithm: theoretical foundations, analysis, and applications. In: Foundations of computational intelligence. Springer, pp 23–55

  61. Dorigo M, Birattari M (2010) Ant colony optimization. Springer, Boston

    Google Scholar 

  62. Gandomi AH, Alavi AH (2012) Krill herd: a new bio-inspired optimization algorithm. Commun Nonlinear Sci Numer Simul 17(12):4831–4845

    MathSciNet  MATH  Google Scholar 

  63. Gandomi AH, Yang XS, Alavi AH (2013) Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng Comput 29(1):17–35

    Google Scholar 

  64. Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95(5):51–67

    Google Scholar 

  65. Mirjalili S (2016) Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl 27(4):1053–1073

    MathSciNet  Google Scholar 

  66. Abderazek H, Ferhat D, Ivana A (2017) Adaptive mixed differential evolution algorithm for bi-objective tooth profile spur gear optimization. Int J Adv Manuf Technol 90(5):2063–2073

    Google Scholar 

  67. Meng Z, Keshtegar B (2019) Adaptive conjugate single-loop method for efficient reliability-based design and topology optimization. Comput Methods Appl Mech Eng 344(2):95–119

    MathSciNet  MATH  Google Scholar 

  68. Kang Z, Liu PS (2018) Reliability-based topology optimization against geometric imperfections with random threshold model. Int J Numer Methods Eng 115(1):99–116

    MathSciNet  Google Scholar 

  69. Gu X, Lu J, Wang H (2015) Reliability-based design optimization for vehicle occupant protection system based on ensemble of metamodels. Struct Multidiscip Optim 51(2):533–546

    Google Scholar 

  70. Acar E, Haftka RT (2007) Reliability-based aircraft structural design pays, even with limited statistical data. J Aircr 44(3):812–823

    Google Scholar 

  71. Spence SMJ, Gioffre M (2012) Large scale reliability-based design optimization of wind excited tall buildings. Probab Eng Mech 28(4):206–215

    Google Scholar 

  72. Kamjoo V, Eamon CD (2018) Reliability-based design optimization of a vehicular live load model. Eng Struct 168(8):799–808

    Google Scholar 

  73. Jiang C, Han X, Guan F, Li Y (2007) An uncertain structural optimization method based on nonlinear interval number programming and interval analysis method. Eng Struct 29(11):3168–3177

    Google Scholar 

  74. Papadrakakis M, Lagaros ND (2002) Reliability-based structural optimization using neural networks and Monte Carlo simulation. Comput Methods Appl Mech Eng 191(32):3491–3507

    MATH  Google Scholar 

  75. Meng Z, Zhang D, Li G, Yu B (2019) An importance learning method for non-probabilistic reliability analysis and optimization. Struct Multidiscip Optim 59(4):1255–1271

    Google Scholar 

  76. Keshtegar B (2016) Chaotic conjugate stability transformation method for structural reliability analysis. Comput Methods Appl Mech Eng 310(10):866–885

    MathSciNet  MATH  Google Scholar 

  77. Lee JO, Yang YS, Ruy WS (2002) A comparative study on reliability-index and target-performance-based probabilistic structural design optimization. Comput Struct 80(3–4):257–269

    Google Scholar 

  78. Wu YT, Millwater HR, Cruse TA (1990) Advanced probabilistic structural analysis method for implicit performance functions. AIAA J 28(9):1663–1669

    Google Scholar 

  79. Youn BD, Choi KK, Park YH (2003) Hybrid analysis method for reliability-based design optimization. J Mech Des 125(2):221–232

    Google Scholar 

  80. Yang D, Li G, Cheng G (2006) Convergence analysis of first order reliability method using chaos theory. Comput Struct 84(8–9):563–571

    Google Scholar 

  81. Meng Z, Li G, Wang BP, Hao P (2015) A hybrid chaos control approach of the performance measure functions for reliability-based design optimization. Comput Struct 146(1):32–43

    Google Scholar 

  82. Keshtegar B, Hao P (2017) A hybrid self-adjusted mean value method for reliability-based design optimization using sufficient descent condition. Appl Math Model 41(1):257–270

    MathSciNet  MATH  Google Scholar 

  83. Li G, Meng Z, Hu H (2015) An adaptive hybrid approach for reliability-based design optimization. Struct Multidiscip Optim 51(5):1051–1065

    MathSciNet  Google Scholar 

  84. Youn BD, Choi KK, Du L (2005) Adaptive probability analysis using an enhanced hybrid mean value method. Struct Multidiscip Optim 29(2):134–148

    Google Scholar 

  85. Ezzati G, Mammadov M, Kulkarni S (2015) A new reliability analysis method based on the conjugate gradient direction. Struct Multidiscip Optim 51(1):89–98

    MathSciNet  Google Scholar 

  86. Keshtegar B, Hao P (2018) Enriched self-adjusted performance measure approach for reliability-based design optimization of complex engineering problems. Appl Math Model 57(5):37–51

    MathSciNet  MATH  Google Scholar 

  87. Yi P, Zhu Z (2016) Step length adjustment iterative algorithm for inverse reliability analysis. Struct Multidiscip Optim 54(4):999–1009

    MathSciNet  Google Scholar 

  88. Mirjalili S (2015) The ant lion optimizer. Adv Eng Softw 83(5):80–98

    Google Scholar 

  89. Mirjalili S, Mirjalili SM, Hatamlou A (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 27(2):495–513

    Google Scholar 

  90. Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM (2017) Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw 114(12):163–191

    Google Scholar 

  91. Saremi S, Mirjalili S, Lewis A (2017) Grasshopper optimisation algorithm: theory and application. Adv Eng Softw 105(3):30–47

    Google Scholar 

  92. Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69(3):46–61

    Google Scholar 

  93. Eskandar H, Sadollah A, Bahreininejad A, Hamdi M (2012) Water cycle algorithm—a novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct 110–111(11):151–166

    Google Scholar 

  94. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Future Gen Comput Syst 97(8):849–872

    Google Scholar 

  95. Gu L, Yang RJ, Tho CH, Makowski M, Faruque O, Li Y (2001) Optimization and robustness for crashworthiness of side impact. Int J Veh Des 26(4):348–360

    Google Scholar 

  96. Keshtegar B, Lee I (2016) Relaxed performance measure approach for reliability-based design optimization. Struct Multidiscip Optim 54(6):1439–1454

    MathSciNet  Google Scholar 

  97. Jiang C, Qiu H, Li X, Chen Z, Gao L, Li P (2019) Iterative reliable design space approach for efficient reliability-based design optimization. Eng Comput. https://doi.org/10.1007/s00366-018-00691-z

    Article  Google Scholar 

  98. Giraud Moreau L, Lafon P (2002) A comparison of evolutionary algorithms for mechanical design components. Eng Optim 34(3):307–322

    Google Scholar 

  99. Cho TM, Lee BC (2011) Reliability-based design optimization using convex linearization and sequential optimization and reliability assessment method. Struct Saf 33(1):42–50

    MathSciNet  Google Scholar 

  100. Chen ZZ, Li XK, Chen G, Gao L, Qiu HB, Wang SZ (2018) A probabilistic feasible region approach for reliability-based design optimization. Struct Multidiscip Optim 57(1):359–372

    MathSciNet  Google Scholar 

  101. Lee JJ, Lee BC (2005) Efficient evaluation of probabilistic constraints using an envelope function. Eng Optim 37(2):185–200

    Google Scholar 

  102. Hao P, Wang YT, Liu C, Wang B, Wu H (2017) A novel non-probabilistic reliability-based design optimization algorithm using enhanced chaos control method. Comput Methods Appl Mech Eng 318(5):572–593

    MathSciNet  MATH  Google Scholar 

  103. Papadopoulos V, Lagaros ND (2009) Vulnerability-based robust design optimization of imperfect shell structures. Struct Saf 31(6):475–482

    Google Scholar 

Download references

Acknowledgements

The supports of the National Natural Science Foundation of China (Grant Nos. 11972143 and 11602076) and the Fundamental Research Funds for the Central Universities of China (Grant No. JZ2020HGPA0112) are much appreciated.

Author information

Authors and Affiliations

  1. School of Civil Engineering, Hefei University of Technology, Hefei, 230009, People’s Republic of China

    Zeng Meng & Xuan Wang

  2. Department of Engineering Mechanics, State Key Laboratory of Structural Analyses for Industrial Equipment, Dalian University of Technology, Dalian, 116024, People’s Republic of China

    Zeng Meng & Gang Li

  3. Department of Computer Engineering, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia

    Sadiq M. Sait

  4. Department of Automotive Engineering, Bursa Uludağ University, Görükle, Bursa, Turkey

    Ali Rıza Yıldız

Authors
  1. Zeng Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xuan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sadiq M. Sait
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ali Rıza Yıldız
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ali Rıza Yıldız.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 RBDO for Automobile Side Impact Case

The RBDO model for automobile side impact case is expressed as:

$$\begin{aligned} & {\text{find}}\quad {\mathbf{d}} = [d_{1} ,d_{2} ,d_{3} ,d_{4} ,d_{5} ,d_{6} ,d_{7} ,d_{8} ,d_{9} ]^{\text{T}} \\ & \hbox{min} \quad {\text{obj}}({\varvec{\upmu}}_{{\mathbf{x}}} ) \\ & {\text{s.t.}} \quad \quad P(F_{AL} \le 1 \,{\mathbf{KN}}) \ge R_{1} \\ & \quad \quad \quad P(D_{up} \le 32\,{\text{cm}}) \ge R_{2} \\ & \quad \quad \quad P(D_{mid} \le 32\,{\text{cm}}) \ge R_{3} \\ & \quad \quad \quad P(D_{low} \le 32\,{\text{cm}}) \ge R_{4} \\ & \quad \quad \quad P({\text{VC}}_{up} \le 0.32\,{\text{cm}}) \ge R_{5} \\ & \quad \quad \quad P({\text{VC}}_{mid} \le 0.32\,{\text{cm}}) \ge R_{6} \\ & \quad \quad \quad P({\text{VC}}_{low} \le 0.32\,{\text{cm}}) \ge R_{7} \\ & \quad \quad \quad P(F_{\text{ps}} \le 4.0 {\mathbf{KN}}) \ge R_{8} \\ & \quad \quad \quad P(V_{\text{B - Pillar}} \le 9.9\,{\text{m/s}}) \ge R_{9} \\ & \quad \quad \quad P(V_{\text{door}} \le 15.69\,{\text{m/s}}) \ge R_{10} \\ & \quad \quad \quad {\varvec{\upmu}}_{i}^{L} \le {\varvec{\upmu}}_{i} \le {\varvec{\upmu}}_{i}^{U} ,\quad i = 1\sim 7 \\ \end{aligned}$$

where

$$\begin{aligned} & {\text{obj}} = 1.98 + 4.9x_{1} + 6.67x_{2} + 6.98x_{3} + 4.01x_{4} + 1.78x_{5} + 2.73x_{7} \\ & F_{AL} = 1.16 - 0.3717x_{2} x_{4} - 0.00931x_{2} x_{10} - 0.484x_{3} x_{9} + 0.01343x_{6} x_{10} \\ & D_{up} = 28.98 + 3.818x_{3} - 4.2x_{1} x_{2} + 0.0207x_{5} x_{10} + 6.63x_{6} x_{9} - 7.77x_{7} x_{8} + 0.32x_{9} x_{10} \\ & D_{mid} = 33.86 + 2.95x_{3} + 0.1792x_{10} - 5.057x_{1} x_{2} - 11x_{2} x_{8} - 0.0215x_{5} x_{10} - 9.98x_{7} x_{8} + 22x_{8} x_{9} \\ & D_{low} = 46.36 - 9.9x_{2} - 12.9x_{1} x_{8} + 0.1107x_{3} x \\ & VC_{up} = 0.261 - 0.0159x_{1} x_{2} - 0.188x_{1} x_{8} - 0.019x_{2} x_{7} + 0.0144x_{3} x_{5} + 0.8757x_{5} x_{10} + 0.08045x_{6} x_{9} \\ & \quad \quad \quad + 0.00139x_{8} x_{11} + 1.575(10^{ - 6} )x_{10} x_{11} \\ & VC_{mid} = 0.214 + 0.00817x_{5} - 0.131x_{1} x_{8} - 0.0704x_{1} x_{9} + 0.03099x_{2} x_{6} - 0.018x_{2} x_{7} \\ & \quad \quad \quad + 0.0208x_{3} x_{8} + 0.121x_{3} x_{9} - 0.00364x_{5} x_{6} + 0.0007715x_{5} x_{10} - 0.0005354x_{6} x_{10} \\ & \quad \quad \quad + 0.00121x_{8} x_{11} + 0.00184x_{9} x_{10} - 0.02x_{2} x_{2} \\ & VC_{low} = 0.74 - 0.61x_{2} - 0.163x_{3} x_{8} + 0.001232x_{3} x_{10} - 0.166x_{7} x_{9} + 0.227x_{2} x_{2} \\ & F_{ps} = 4.72 - 0.5x_{4} - 0.19x_{2} x_{3} - 0.0122x_{4} x_{10} + 0.009325x_{6} x_{10} + 0.000191x_{11} x_{11} \\ & V_{B - Pillar} = 10.58 - 0.674x_{1} x_{2} - 1.95x_{2} x_{8} + 0.02054x_{3} x_{10} - 0.0198x_{4} x_{10} + 0.028x_{6} x_{10} \\ & V_{door} = 16.45 - 0.489x_{3} x_{7} - 0.843x_{5} x_{6} + 0.0432x_{9} x_{10} - 0.0556x_{9} x_{11} - 0.000786x_{11} x_{11} \\ \end{aligned}$$

where \(R_{1} { = }R_{2} = \cdots = R_{11} = \varPhi (3)\)

$$x_{i} \sim N(1,0.03^{2} ) ,i = 1 - 7, i \ne 5;\,x_{5} \sim N(2,0.05^{2} );\,x_{i} \sim N(0.192,0.06^{2} ),i = 8\,{\text{and}}\,9;$$
$$x_{i} \sim N(0,10^{2} ) , i = 10 {\text{and}} 11$$
$$0.5 \le x_{i} \le 1.5, i = 1,3,4; 0.45 \le x_{2} \le 1.35; 0.875 \le x_{5} \le 2.625; 0.4 \le x_{6} \le 1.2; 0.4 \le x_{7} \le 1.2\,x_{8} ,x_{9} \in (0.192,0.345).$$

1.2 RBDO for a Bolted Rim

The RBDO model for bolted rim is formulated as (Table 8):

Table 8 Discrete values of bolts d
Full size table
$$\begin{aligned} & {\text{find}}\quad {\mathbf{d}} = [R_{B} ,M,d,N]^{\text{T}} \\ & \hbox{min} \quad f\left( {\mathbf{d}} \right) = \beta_{1} \left( {\frac{N}{{N_{m} }}} \right) + \beta_{2} \left( {\frac{{R_{B} + \phi_{4} (d) + c}}{{R_{m} }}} \right) + \beta_{3} \left( {\frac{M}{{M_{T} }}} \right) \\ & {\text{s.t.}}\quad P[G_{i} ({\mathbf{x}}) > 0] \ge \varPhi (\beta_{i}^{t} );\quad i = 1 - 11. \\ & G_{1} ({\mathbf{x}}) = 1 - \frac{\alpha M}{{NR_{B} K(d)}} \ge 0,\quad \quad G_{2} ({\mathbf{x}}) = \frac{{2\pi R_{B} }}{{\phi_{5} (d)N}} - 1 \ge 0 \\ & G_{3} ({\mathbf{x}}) = \frac{{R_{B} }}{{\phi_{4} (d)}} + R_{M} - 1 \ge 0,\quad \quad G_{4} ({\mathbf{x}}) = N_{\hbox{max} } - N \ge 0 \\ & G_{5} ({\mathbf{x}}) = R_{\hbox{max} } - R_{B} \ge 0,\quad \quad G_{6} ({\mathbf{x}}) = N - N_{M} \ge 0 \\ & G_{7} ({\mathbf{x}}) = R_{B} - R_{M} \ge 0,\quad \quad G_{8} ({\mathbf{x}}) = M_{\hbox{max} } - M \ge 0 \\ & G_{9} ({\mathbf{x}}) = M - M_{T} \ge 0,\quad \quad G_{10} ({\mathbf{x}}) = 24 - d \ge 0 \\ & G_{11} ({\mathbf{x}}) = d - 6 \ge 0 \\ & \beta_{1}^{t} = \beta_{2}^{t} = \cdot \cdot \cdot = \beta_{11}^{t} = 3.0,\; \\ \end{aligned}$$

where \(R_{B} \sim N(60,1),M\sim N(60,1)\)

$$K(d) = \frac{{0.9f_{m} R_{e} \pi \left( {\phi_{1} (d)} \right)^{2} }}{{4\sqrt {1 + 3(0.16\phi_{3} (d)f_{1} /\phi_{1} (d))^{2} } }}, \, M_{T} = 40\,{\text{Nm}}, \, M_{\hbox{max} } = 1000\,{\text{Nm}},f_{m} = 0.15,$$
$$\, f_{1} = 0.15,\alpha = 1.5, \, R_{e} = 627\,{\text{MPa}}, \, N_{M} = 8, \, N_{\hbox{max} } = 100, \, R_{M} = 50\,{\text{mm}}, \, R_{\hbox{max} } = 1000\,{\text{mm}},c = 5\,{\text{mm}}, \, \beta_{1} = \beta_{2} = \beta_{3} = 1$$
$$6 \le d \le 24 , { }8 \le N \le 100, \, 50 \le R_{B} \le 100,40 \le M \le 100.$$

1.3 RBDO for Spur Speed Reducer

The RBDO model for spur speed reducer is depicted as:

$$\begin{aligned} & {\text{find}}\quad {\mathbf{d}} = [\mu_{{x_{1} }} ,\mu_{{x_{2} }} ,\mu_{{x_{3} }} ,\mu_{{x_{4} }} ,\mu_{{x_{5} }} ,\mu_{{x_{6} }} ,\mu_{{x_{7} }} ]^{\text{T}} \\ & \hbox{min} \quad f({\mathbf{d}}) = 0.7854\mu_{{x_{1} }} \mu_{{x_{2} }}^{2} \left( {3.3333\mu_{{x_{3} }}^{2} + 14.9334\mu_{{x_{3} }}^{{}} - 43.0934} \right) \\ & \quad \quad \; - 1.508\mu_{{x_{1} }} \left( {\mu_{{x_{6} }}^{2} + \mu_{{x_{7} }}^{2} } \right) + 7.477\left( {\mu_{{x_{6} }}^{3} + \mu_{{x_{7} }}^{3} } \right) + 0.7854\left( {\mu_{{x_{4} }} \mu_{{x_{6} }}^{2} + \mu_{{x_{5} }} \mu_{{x_{7} }}^{2} } \right) \\ & {\text{s.t.}} \quad \quad {\text{P}}\left[ {G_{i} ({\mathbf{x}}) > 0} \right] \ge \varPhi \left( {\beta_{i}^{t} } \right); i = 1 - 11. \\ & G_{1} ({\mathbf{x}}) = \frac{27}{{x_{1} x_{2}^{2} x_{3} }} - 1, G_{2} ({\mathbf{x}}) = \frac{397.5}{{x_{1} x_{2}^{2} x_{3}^{2} }} - 1 \\ & G_{3} ({\mathbf{x}}) = \frac{{1.93x_{4}^{3} }}{{x_{2} x_{3} x_{6}^{4} }} - 1, G_{4} ({\mathbf{x}}) = \frac{{1.93x_{5}^{3} }}{{x_{2} x_{3} x_{7}^{4} }} - 1 \\ & G_{5} ({\mathbf{x}}) = \frac{{\sqrt {\left( {{{745x_{4} } \mathord{\left/ {\vphantom {{745x_{4} } {(x_{2} x_{3} )}}} \right. \kern-0pt} {(x_{2} x_{3} )}}} \right)^{2} + 16.9 \times 10^{6} } }}{{0.1x_{6}^{3} }} - 1100 \\ & G_{6} ({\mathbf{x}}) = \frac{{\sqrt {\left( {{{745x_{4} } \mathord{\left/ {\vphantom {{745x_{4} } {(x_{2} x_{3} )}}} \right. \kern-0pt} {(x_{2} x_{3} )}}} \right)^{2} + 157.5 \times 10^{6} } }}{{0.1x_{7}^{3} }} - 850 \\ & G_{7} ({\mathbf{x}}) = x_{2} x_{3} - 40, G_{8} ({\mathbf{x}}) = 5 - \frac{{x_{1} }}{{x_{2} }} \\ & G_{9} ({\mathbf{x}}) = \frac{{x_{1} }}{{x_{2} }} - 12, G_{10} ({\mathbf{x}}) = \frac{{1.5x_{6} + 1.9}}{{x_{4} }} - 1 \\ & G_{11} ({\mathbf{x}}) = \frac{{1.1x_{7} + 1.9}}{{x_{5} }} - 1 \\ & \beta_{1}^{t} = \beta_{2}^{t} = \cdots = \beta_{11}^{t} = 3.0 \\ & 2.6 \le \mu_{{x_{1} }} \le 3.6,\;0.7 \le \mu_{{x_{2} }} \le 0.8,17 \le \mu_{{x_{3} }} \le 28 \\ & 7.3 \le \mu_{{x_{4} }} \le 8.3,\;\;7.3 \le \mu_{{x_{5} }} \le 8.3 \\ & 2.9 \le \mu_{{x_{6} }} \le 3.9,\;5.0 \le \mu_{{x_{7} }} \le 5.5 \\ & x_{i} \sim N(\mu_{{x_{i} }} , 0.005^{2} ),\quad {\text{for}} \;i = 1 - 7. \\ \end{aligned}$$

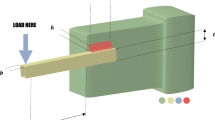
1.4 RBDO for Welded Beam

The RBDO model for welded beam is expressed as:

$$\begin{aligned} & {\text{find}}\quad {\mathbf{d}} = [d_{1} ,d_{2} ,d_{3} ,d_{4} ] \\ & \hbox{min} \quad \,f\left( {{\mathbf{d}},{\mathbf{z}}} \right) = c_{1} d_{1}^{2} d_{2} + c_{2} d_{3} d_{4} (z_{2} + d_{2} ) \\ & {\text{s.t.}}\quad \; P(G_{i} \left( {{\mathbf{x}},{\mathbf{z}}} \right) > 0) \ge \varPhi \left( {\beta_{i}^{t} } \right),\,\,i = 1, \ldots ,5 \\ & {\text{where}}\,\,G_{1} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = {{\tau ({\mathbf{x}},{\mathbf{z}})} \mathord{\left/ {\vphantom {{\tau ({\mathbf{x}},{\mathbf{z}})} {z_{6} }}} \right. \kern-0pt} {z_{6} }} - 1,\;\;G_{2} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = {{\sigma \left( {{\mathbf{x}},{\mathbf{z}}} \right)} \mathord{\left/ {\vphantom {{\sigma \left( {{\mathbf{x}},{\mathbf{z}}} \right)} {z_{7} }}} \right. \kern-0pt} {z_{7} }} - 1, \\ & \quad \quad G_{3} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {x_{4} }}} \right. \kern-0pt} {x_{4} }} - 1,\;\;\;G_{4} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = {{\delta \left( {{\mathbf{x}},{\mathbf{z}}} \right)} \mathord{\left/ {\vphantom {{\delta \left( {{\mathbf{x}},{\mathbf{z}}} \right)} {z_{5} - 1,}}} \right. \kern-0pt} {z_{5} - 1,}} \\ & \quad \quad G_{5} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = 1 - P_{c} \left( {{\mathbf{x}},{\mathbf{z}}} \right)/z_{1} , \\ & \quad \quad \tau \left( {{\mathbf{x}},{\mathbf{z}}} \right) = \{ t\left( {{\mathbf{x}},{\mathbf{z}}} \right)^{2} + \frac{{2t\left( {{\mathbf{x}},{\mathbf{z}}} \right)tt\left( {{\mathbf{x}},{\mathbf{z}}} \right)X_{2} }}{{2R\left( {\mathbf{x}} \right)}} + tt\left( {{\mathbf{x}},{\mathbf{z}}} \right)^{2} \}^{1/2} , \\ & \quad \quad t\left( {{\mathbf{x}},{\mathbf{z}}} \right) = \frac{{z_{1} }}{{\sqrt 2 x_{1} x_{2} }},\;\;tt\left( {{\mathbf{x}},{\mathbf{z}}} \right) = \frac{{M\left( {{\mathbf{x}},{\mathbf{z}}} \right)R\left( {\mathbf{x}} \right)}}{{J\left( {\mathbf{x}} \right)}}, \\ & \quad \quad \sigma \left( {{\mathbf{x}},{\mathbf{z}}} \right) = \frac{{6z_{1} z_{2} }}{{x_{3}^{2} x_{4} }},\;\;\delta \left( {{\mathbf{x}},{\mathbf{z}}} \right) = \frac{{4z_{1} z_{2}^{3} }}{{z_{3} x_{3}^{3} x_{4} }}, \\ & \quad \quad M\left( {{\mathbf{x}},{\mathbf{z}}} \right) = z_{1} \left( {z_{2} + \frac{{x_{2} }}{2}} \right),\;\;R\left( {\mathbf{x}} \right) = \left( {\frac{{\sqrt {x_{2}^{2} + (x_{1} + x_{3} )^{2} } }}{2}} \right), \\ & \quad \quad J\left( {\mathbf{x}} \right) = \sqrt 2 x_{1} x_{2} \left\{ {{{x_{2}^{2} } \mathord{\left/ {\vphantom {{x_{2}^{2} } {12}}} \right. \kern-0pt} {12}} + {{\left( {x_{1} + x_{3} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {x_{1} + x_{3} } \right)^{2} } 4}} \right. \kern-0pt} 4}} \right\}, \\ & \quad \quad P_{c} \left( {{\mathbf{x}},{\mathbf{z}}} \right) = \frac{{4.013x_{3} x_{4}^{3} \sqrt {z_{3} z_{4} } }}{{6z_{2}^{2} }}\left( {1 - \frac{{x_{3} }}{{4z_{2} }}\sqrt {\frac{{z_{3} }}{{z_{4} }}} } \right), \\ & \quad \quad \beta_{1}^{t} = \beta_{2}^{t} = \cdots = \beta_{5}^{t} = 3.0,\; \\ & \quad \quad 3.175 \le d_{1} \le 50.8,\;0 \le d_{2} \le 254, \\ & \quad \quad 0 \le d_{3} \le 254,\;\;0 \le d_{4} \le 50.8 \\ & \quad \quad x_{i} \sim N(d_{i} ,0.1693^{2} )\quad {\rm for}\;i = 1,2, \\ & \quad \quad x_{i} \sim N(d_{i} ,0.0107^{2} )\quad {\rm for}\;i = 3,4. \\ \end{aligned}$$

1.5 RBDO for Stiffened Shell

The RBDO for stiffened shell is expressed as:

$$\begin{aligned} & {\text{find}} \quad {\mathbf{d}} = [t_{s}^{C} ,\,t_{r}^{C} ,h_{{}}^{C} ,N_{c} ,N_{a} ]^{\text{T}} \\ & \mathop {\hbox{min} }\limits_{{}} \quad f({\mathbf{d}}) \\ & {\text{s.t.}}\quad P({\text{load(}}t_{s} ,t_{r} ,h,N_{c} ,N_{a} ,E,\nu ) - 1.2747 \times 10^{7} > 0) \ge \varPhi (\beta_{{}}^{t} ) \\ & \quad \quad 2.5 \le t_{s} \le 5.5,6.0 \le t_{r} \le 12.0,9.0 \le h \le 23.0 \\ & \quad \quad 10 \le N_{c} \le 38;80 \le N_{a} \le 130,\beta_{{}}^{t} = 3. \\ \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Meng, Z., Li, G., Wang, X. et al. A Comparative Study of Metaheuristic Algorithms for Reliability-Based Design Optimization Problems. Arch Computat Methods Eng 28, 1853–1869 (2021). https://doi.org/10.1007/s11831-020-09443-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-020-09443-z

Search

Navigation