1 Introduction

In the broad subject of wave-energy extraction, various control strategies have been proposed and implemented on single or stand-alone wave-energy converters, including resistive control, approximate complex-conjugate control, and phase control by latching or clutching (see for example, Bacelli et al. (2016) and Hals et al. (2011a)). As commercialization of wave energy will eventually be realized by farms of WECs, the development of control strategies for a WEC array is of high importance for improving the overall efficiency.

As waves scattered around each individual body, hydrodynamics of an array will differ from a group of isolated bodies, which affects power-capture capability and the control strategy that needs to be applied to the array. Evans (1979) and Falnes (1980) independently provided general formulas for the power-capture characteristics of an array of oscillating WECs using frequency-domain analysis, in the context of linear wave theory. The optimal power can be achieved by applying complex-conjugate control to the array. In their works, an interaction factor, named q factor, was introduced to represent the ratio of the power captured by an array to that captured by the sum from each member element acting in isolation. This approach was then applied in various studies of power absorption of different WEC arrays (Thomas and Evans 1981; Evans 1981; Falnes and Budal 1982; McIver 1994) with or without motion constraints on the devices. However, since the focus was on just the theoretical limit of the power generated by a given array, not many control strategies were developed for engineering applications other than resistive loading and complex-conjugate control, which have inherent difficulties in handling constraints and in achieving physically the required off-diagonal values in the damping matrix of the array. Further, in order to apply the theory for obtaining the optimal operating condition, hydrodynamic properties including wave-exciting forces, radiation damping coefficients, etc., for each individual device in the array configuration are needed. This can be a complex hydrodynamic problem itself with waves radiating and diffracting from one and another. Point-absorber theory has been used to approximate wave-interaction effects, which considers only the effect of radiation waves from one body on the others, but the diffracting waves, caused by the incident waves existing among the array, are neglected for convenience. More accurate methods include plane-wave theory (Simon 1982) where scattering waves were assumed to be plane waves; multiple scattering waves (Ohkusu 1974) where a multilevel iterative scheme was proposed to consider higher orders of scattering waves; and an algebraic exact interaction theory (Kagemoto and Yue 1986), where a direct matrix method was applied to find the hydrodynamics of the array using the diffraction properties of individual members. More recently, a generalized formulation for handling this issue was presented (Zhong and Yeung 2016). These methods can achieve different orders of interaction accuracy. However, for some, the computational cost can be prohibitively high for real-time implementation. The hydrodynamic interaction theory is not the focus here.

Recently, control of an array with physical and machinery constraints and wave-interaction effects taken into account is attracting more and more attention, which is attributed to the development of optimal control strategies for single WECs and the rapid increase in computing power. A model-based control strategy was developed and applied to unconstrained and constrained devices globally or independently (Barcelli and Ringwood 2013). The global controller optimized the performance of the whole system and operated each device in a coordinated manner, while the independent controller was used on an individual device with the knowledge of the surrounding wave field, but not of the actions of controllers on the other devices. Hydrodynamic coefficients were computed by the boundary element solver WAMIT which considers full wave interactions. It was shown that 10% or more performance improvement can be achieved for a WEC array by using the coordinated control, compared to the independent control. Li implemented decentralized, centralized, and distributed model predictive control (MPC) to an array of two WECs (Li and Belmont 2014a, b) with the point-absorber theory mentioned above to account for wave-interaction effects. For distributed MPC, each WEC was equipped with one controller and all the controllers were coordinated and run iteratively to achieve an optimal solution for the whole system. It was found by these authors that the distributed MPC can achieve almost the same amount of energy as that of the centralized MPC where the optimization was performed directly for the system; in the meantime, the former can reduce the computational burden to a large extent.

It is of interest to note that, unlike the case of a single device, the phase of the oscillating velocity of the individual cylinder in an array is not necessarily in phase with the wave-exciting force. The computational cost to find the optimal amplitude and phase of each oscillating body in an array and, most importantly, the control input to achieve the optimal conditions can be prohibitively demanding, especially with constraints being considered simultaneously. Furthermore, if a control strategy is to be implemented online, which better accounts for state changes and rejects disturbances compared to an offline control, the control strategy should be generated in a relatively short amount of time (compared with plant dynamics). MPC has shown its strong potential when applied to single WECs because of its capability in handling hard constraints on both states and the control input (see, e.g., Son et al. 2016). To overcome the challenge of the computational cost, a convex formulation of the optimization problem for the MPC was proposed (Zhong and Yeung 2017). The problem was recast as a quadratic programming (QP) problem, for which convexity can be guaranteed by tuning the weight of the penalty term on slew rates of the control input in the cost function; hence, the problem can be solved efficiently by a standard QP solver.

In this paper, such an MPC (Zhong and Yeung 2017) is applied to an array of WECs, in both regular and irregular waves. Point-absorber approximation will be adopted to simplify the consideration of wave-interaction effects. We will form a central controller to optimize the global performance of the energy absorption with constraints added on the control force and the oscillation amplitude of each device. Performance of the current MPC will be compared with a simple passive control strategy on the array. The interaction factor q of a WEC array under control will be studied, as well as the effects of constraints. In addition, reactive power required by the current MPC will be discussed. As the MPC requires that a wave-prediction unit be simultaneously incorporated to predict the dynamics of the system, we will assume in this work that there exists a wave predictor (Fusco and Ringwood 2012; Morris et al. 1998), which can estimate the wave elevation at a designated location for a certain future period.

2 Modeling of an Array of Point Absorbers

Figure 1 shows an artist conception of a farm of wave-energy devices which can act independently in a seaway or in a coordinated manner with possible communication among themselves. Ideally, we assume the incident-wave field is known and if a global controller is intelligent enough; the system may act cohesively to achieve the best global performance subject to some hardware or physical constraints. It is not difficult to envision each device may have its own controller communicating with a global controller. In what follows, we set up a framework so that the master controller would direct the members to act in the best interest of the “community.”

Fig. 1
figure 1

Artist conception of a community of WEC working in consonance, in communication with a global controller or among one another (artwork credit & copyright, 2018: Lu Wang, Ph.D.)

Full size image

2.1 The Equations of Motion

Without loss of generality, we consider the bodies in the array to be different in size. In the time domain, the equation of motion of the j th heaving point absorber in an array of N bodies can be written as follows:

$$ m_{j}{\ddot{\zeta}}_{3}^{j} = {{f}_{e}^{j}}(t) + {{f}_{r}^{j}}(t) + {{f}_{h}^{j}}(t) + {{f}_{m}^{j}}(t) $$
(1)

where mj and \({{\zeta }_{3}^{j}}(t)\) are mass and heave displacement of the absorber. Here, \({{f}_{e}^{j}}(t)\), \({{f}_{r}^{j}}(t)\), \({{f}_{h}^{j}}(t)\), and \({{f}_{m}^{j}}(t)\) are wave-exciting, wave-radiation, hydrostatic restoring, and machinery forces on the cylinder j, respectively, where \({{f}_{h}^{j}}(t)\) and \({{f}_{r}^{j}}(t)\) can take the form as follows:

$$\begin{array}{@{}rcl@{}} {{f}_{h}^{j}}(t) &=& -K_{j} {\zeta^{j}_{3}}(t) \end{array} $$
(2a)
$$\begin{array}{@{}rcl@{}} {{f}_{r}^{j}}(t) &=& -\mu^{j}_{33}(\infty) \ddot{\zeta}^{j}_{3}(t) - \lambda^{j}_{33}(\infty) \dot{\zeta}^{j}_{3}(t)\\ &&- \sum\limits_{l = 1}^{N} {\int}_{\!\!\!\!-\infty}^{t} {K}_{r}^{jl}(t-\tau){\dot{\zeta}}_{3}^{k}(\tau) \mathrm{d}\tau \end{array} $$
(2b)

where Kj is the hydrostatic stiffness coefficient, \({\mu }_{33}^{j}\) and \({\lambda }_{33}^{j}\) are added-mass and damping coefficients at infinite frequency; note that \({\lambda }_{33}^{j}(\infty ) = 0\). The convolution integrals represent the fluid memory effects where \({K}_{r}^{jl}(t)\) is the impulse response function with the superscripts jl indicating the effect of cylinder l on cylinder j. The \({K}_{r}^{jl}\) can be obtained by the inverse Fourier transform of the damping coefficients in frequency domain (Wehausen 1971) as follows:

$$ {K}_{r}^{jl}(t) = \frac{2}{\uppi}{\int}_{\!\!\!\!0}^{\infty} \left[{\lambda}_{33}^{jl}(\sigma)-{\lambda}_{33}^{jl}(\infty)\right]\cos(\sigma t) \mathrm{d}\sigma $$
(3)

where wave damping at infinite frequency vanishes, i.e., \({\lambda }_{33}^{jl}(\infty ) = 0\). For l ≠ j, the \({\lambda }_{33}^{jl}\) represents the effect of the motion of the cylinder k on the wave forces of cylinder j, which will be discussed in detail in Section 2.2. The wave-exciting force can be expressed as follows:

$$ f_{e}(t) = {\int}_{\!\!\!\!-\infty}^{\infty} K_{e}(t-\tau)\eta(0,t) \mathrm{d}\tau , $$
(4)

for a given η(0, t), the incident-wave elevation at the vertical axis of the body. The impulse response function Ke(t) can be evaluated by the inverse Fourier transform of the complex amplitude X3 of the wave-exciting force induced by unit-amplitude waves of frequency σ as follows:

$$ K_{e}(t) = \frac{1}{2\uppi}\Re\left\{ {\int}_{\!\!\!\!-\infty}^{\infty} X_{3}(\sigma)\mathrm{e}^{\mathrm{i}\sigma t}\mathrm{d}\sigma \right\} $$
(5)

As full knowledge of the incoming waves is presumed in this paper, we will compute the wave forces based on the frequency-domain analysis under linear wave theory, for regular waves in Section 4.1 and for irregular waves in Section 4.2.

Substituting Eqs. 2a and 2b into Eq. 1, we obtain the following:

$$\begin{array}{@{}rcl@{}} &&(m_{j}+{\mu}_{33}^{j}(\infty)){\ddot{\zeta}}_{3}^{j}(t) + \lambda_{\text{vis}}{\dot{\zeta}}_{3}^{j} + K_{j} {{\zeta}_{3}^{j}}(t)\\ &&+ \sum\limits_{l = 1}^{N} {\int}_{-\infty}^{t} {K}_{r}^{jl}(t-\tau){\dot{\zeta}}_{3}^{k}(\tau) \mathrm{d}\tau = {{f}_{e}^{j}}(t) + {{f}_{m}^{j}}(t) \end{array} $$
(6)

where a corrective linear-viscous damping coefficient λvis, obtained from experiments (Tom and Yeung 2014), is included to account for viscosity-based dissipation.

2.2 Point-Absorber Approximation

To model the wave-interaction effect among an array, we adopt the point-absorber approximation (Evans 1979; Falnes 1980) which simplifies the hydrodynamic interaction problem but considers the effect of the radiating waves from one device on the other devices. As indicated by McIver (1994), the basic assumption of this approximation is that the devices are small enough, relative to the wavelength of the incident waves, for the structure to be a weak scatterer. Based on this, all scattered waves were neglected in the computation of interaction effects. Hence, the wave-exciting force on an individual cylinder is the same as the one on an isolated body except for a possible phase change governed by the coordinate origin of the cylinder. The damping coefficient \({\lambda }_{33}^{jj}\) representing the hydrodynamic force induced by the motion of the j th cylinder itself will also not be affected by interacting waves. However, the “interaction” damping coefficient \({\lambda }_{33}^{jl}\) with j ≠ l, representing the force on the body j caused by the motion of the body k, will need to be evaluated. Following the derivation by Evans (1979), we can obtain the interaction damping coefficients \({\lambda }_{33}^{jl}\) for the j th cylinder located at a global (cylindrical) coordinates (rj, αj) induced by the l th cylinder located at (rl, αl) as follows:

$$ {\lambda}_{33}^{jl} = \lambda_{33} J_{0}(kd_{jl}) $$
(7)

where λ33 is the radiation damping coefficient for the isolated cylinder, J0 is the zero-th-order Bessel function, k is the wave number of the incoming waves, and \({ d_{jl} = \sqrt {{r_{j}^{2}}+{r_{l}^{2}} - 2r_{j} r_{l} \cos (\alpha _{m} - \alpha _{n})}} \) is the distance between the j th and l th body with j, l = 1, 2, … , N. Note that \({\lambda }_{33}^{jl} = \lambda _{33}\) if j = l, and \({\lambda }_{33}^{jl} = {\lambda }_{33}^{lj}\). Substitution of Eq. 7 into Eq. 3 yields the retardation function \(K_{r}^{jl}(t)\). In addition, as derived by Evans (1979), the complex amplitude \({X}_{3}^{j}\) of the wave-exciting force on cylinder j with a phase shift because of the location of the cylinder j can be obtained by the following:

$$ {X}_{3}^{j}(\sigma) = X_{3}(\sigma)\mathrm{e}^{\mathrm{i}kr_{j} \cos(\beta-\alpha_{j})} $$
(8)

where β is the incident angle of the waves measured from the x-axis and X3 for the isolated cylinder, which can be obtained from frequency-domain hydrodynamic analysis (Wehausen 1971).

2.3 State-Space Model

To form the state-space model based on the equation of motion (6), we denote the convolution of \({K}_{r}^{jl}\) and \(\dot {\zeta }_{3}(t)\) by \({y}_{r}^{jl}\), and approximate it using the following linear subsystem:

$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{z}}^{jl}_{r}(t) &=& {A}_{r}^{jl} {\boldsymbol{z}}_{r}^{jl}(t) + {B}_{r}^{jl} {\dot{\zeta}}_{3}^{l}(t) \end{array} $$
(9a)
$$\begin{array}{@{}rcl@{}} {y}_{r}^{jl} &=& {C}_{r}^{jl} {\boldsymbol{z}}_{r}^{jl}(t) + {D}_{r}^{jl}(t) {\dot{\zeta}}_{3}^{l}(t) \end{array} $$
(9b)

where \({z}_{r}^{jl} \in {\mathbb {R}}^{{n}_{r}^{jl}}\) with \({n}_{r}^{jl}\) being the number of states in this model. Since \({\lambda }_{33}^{jl} = {\lambda }_{33}^{lj}\) which implies \({K}_{r}^{jl} = {K}_{r}^{lj}\) per Eq. 3, the two can be modeled by the same subsystem, i.e., \({A}_{r}^{jl} = {A}_{r}^{lj}\), \({B}_{r}^{jl} = {B}_{r}^{lj}\), \({C}_{r}^{jl} = {C}_{r}^{lj}\), and \({D}_{r}^{jl} = {D}_{r}^{lj}\). A reduced-order model obtained by MATLAB function balmr was used to reduce the number of states and in the meantime capture the charateristics of the impulse responses. Substituting Eqs. 9a and 9b into Eq. 6 and using \({\boldsymbol {x}_{j} = \left [{{\zeta }_{3}^{j}}, \dot {\zeta }_{3}^{j},{\boldsymbol {z}}_{r}^{jj}, {\boldsymbol {z}}_{r}^{j1},\dots ,{\boldsymbol {z}}_{r}^{jl},\dots ,{\boldsymbol {z}}_{r}^{jN}\right ]}\) (l ≠ j) as the state vector, we can write the equation of motion for the j th cylinder as follows:

$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{x}}^{j} &=& A_{j} \boldsymbol{x}^{j} + \sum\limits_{l = 1, l\neq j}^{N} F_{jl} \boldsymbol{x}^{l} + B_{j} \left( u^{j} + w^{j}\right) \end{array} $$
(10a)
$$\begin{array}{@{}rcl@{}} y^{j} &=& C_{j} \boldsymbol{x}^{j} \end{array} $$
(10b)
$$\begin{array}{@{}rcl@{}} z^{j} &=& C_{z,j} \boldsymbol{x}^{j} \end{array} $$
(10c)

where \(y^{j} := \dot {\zeta }^{j}_{3}\), \(z^{j} := {{\zeta }_{3}^{j}}\), \(u^{j} := {{f}_{m}^{j}}\), \(w^{j} := {{f}_{e}^{j}}\), and

figure a
figure b
$$\begin{array}{@{}rcl@{}} B_{j} &=& \left[0, 1/M, \boldsymbol{0}_{1\times {{N}_{r}^{j}}}\right]^{T}\\ C_{j} &=& \left[0, 1, \boldsymbol{0}_{1 \times {{N}_{r}^{j}}}\right], \quad C_{z,j} = \left[1, 0, \boldsymbol{0}_{1 \times {{N}_{r}^{j}}}\right] \end{array} $$

where \(M := m_{j}+{\mu }_{33}^{j}(\infty )\), \({B}_{r}^{jl}\) is in the same row as \({A}_{r}^{jl}\), and \({{N}_{r}^{j}} = \sum \limits _{l = 1,l\neq j}^{N} {n}_{r}^{jl}\) is the total number of states for the “interaction” radiation subsystems.

The centralized model for a system of N WECs can be written as

$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{x}} &=& A \boldsymbol{x} + B (\boldsymbol{u} + \boldsymbol{w}) \end{array} $$
(11a)
$$\begin{array}{@{}rcl@{}} \boldsymbol{y} &=& C \boldsymbol{x} \end{array} $$
(11b)
$$\begin{array}{@{}rcl@{}} \boldsymbol{z} &=& C_{z} \boldsymbol{x} \end{array} $$
(11c)

where x = [x1;x2;…;xN], u = [u1;u2;…;uN], w = [w1;w2;…;wN], and

$$\begin{array}{@{}rcl@{}} A_{c} &=& \left[\begin{array}{cccccc} A_{1}\quad & F_{12}\quad & \dots\quad & \dots\quad & F_{1N} \\ F_{21}\quad & A_{2}\quad & F_{23}\quad & \dots\quad & F_{2N} \\ F_{31}\quad & F_{32}\quad & A_{3}\quad & \dots\quad & F_{3N} \\ \vdots\quad & \vdots\quad & \vdots\quad & \ddots\quad & {\vdots} \\ F_{N1}\quad & F_{N2}\quad & F_{N3}\quad & \dots\quad & A_{N} \end{array}\right] \\ B_{c} &=& \text{blkdiag}(B_{1}, B_{2}, \dots, B_{N}) \\ C_{c} &=& \text{blkdiag}(C_{1}, C_{2}, \dots, C_{N}) \\ C_{c,z} &=& \text{blkdiag}(C_{z,1}, C_{z,2}, \dots, C_{z,N}) \end{array} $$
(12)

The state-space model (12) is discretized using zero-order hold (Hals et al. 2011b), where inputs are assumed to be piecewise constant over the sampling time Ts. As a result, we obtain the following discrete-time model:

$$\begin{array}{@{}rcl@{}} \boldsymbol{x}_{k + 1} &=& A \boldsymbol{x}_{k} + B (\boldsymbol{u}_{k} + \boldsymbol{w}_{k} ) \end{array} $$
(13a)
$$\begin{array}{@{}rcl@{}} \boldsymbol{y}_{k} &=& C \boldsymbol{x}_{k} \end{array} $$
(13b)
$$\begin{array}{@{}rcl@{}} \boldsymbol{z}_{k} &=& C_{z} \boldsymbol{x}_{k} \end{array} $$
(13c)

where the subscript k indicates the time instant k.

3 Model-Predictive Control Formulation

With the state-space model constructed in Section 2, we can apply the procedure of the MPC formulation (Zhong and Yeung 2017) to build a MPC controller for multiple WECs.

3.1 The Optimization Problem

The goal is to maximize the total energy E extracted by all of the PTO systems over a predicted time horizon Th, where

$$ E = {\int}_{0}^{T_{h}} P(t) \mathrm{d}t = -{\int}_{0}^{T_{h}} \sum\limits_{j = 1}^{N} {{f}_{m}^{j}}(t) {\dot{\zeta}}_{3}^{j}(t) \mathrm{d}t $$
(14)

With the use of the discrete-time model (13a) and (13b) E can be written as \({E = T_{s} \sum \limits _{k = 0}^{N_{h}-1} \left (-\boldsymbol {u}^{T}_{k} \boldsymbol {y}_{k}\right )}\), where Nh is the number of sampling time instants during the time horizon Th, i.e., Th = NhTs. Hence, the objective is to find a series of inputs uk (k = 0, 1 , … , Nh − 1) such that

$$\begin{array}{@{}rcl@{}} \max_{[\boldsymbol{u}_{0}, \boldsymbol{u}_{1}, \dots, \boldsymbol{u}_{N_{h}-1}]} E &=& \min_{[\boldsymbol{u}_{0}, \boldsymbol{u}_{1}, \dots, \boldsymbol{u}_{N_{h}-1}]} (-E)\\ &=& \min_{[\boldsymbol{u}_{0}, \boldsymbol{u}_{1}, \dots, \boldsymbol{u}_{N_{h}-1}]} T_{s}{\sum}_{k = 0}^{N_{h}-1} \boldsymbol{u}_{k}^{T} \boldsymbol{y}_{k} \end{array} $$
(15)

This is equivalent to setting the cost function to be as follows:

$$ J_{0} = \sum\limits_{k = 0}^{N_{h}-1} {\boldsymbol{u}}_{k}^{T} \boldsymbol{y}_{k} $$
(16)

and minimize J0 over the control inputs. For safety and long-term operation, constraints on the heaving motion of the absorber z and the machinery force u need to be included:

$$\begin{array}{@{}rcl@{}} |{{z}_{k}^{j}}| &\leq& \zeta_{3,\max} \end{array} $$
(17a)
$$\begin{array}{@{}rcl@{}} |{{u}_{k}^{j}}| &\leq& f_{m, \max} \end{array} $$
(17b)

where k = 0, 1, … , Nh − 1 and j = 1, 2, … , N. However, it can be shown that the constrained optimization problem formed by Eqs. 16, 17a and 17b will result in a nonconvex QP (Li and Belmont 2014a), for which the global optimal solution is not guaranteed.

In this paper, we construct the cost function to be as follows:

$$ J = \sum\limits_{k = 0}^{N_{h}-1} \left( {\boldsymbol{u}}_{k}^{T} \boldsymbol{y}_{k} + r || {\Delta} \boldsymbol{u}_{k} {||}_{2}^{2}\right) $$
(18)

where Δuk = uk −uk− 1 for k = 0, 1, 2, … , Nh − 1, and ||⋅||2 represents the l2 norm. Δu0 := u0 −u− 1 where u− 1 is defined as the control input obtained in the previous time horizon, and u− 1 = 0 initially. The convexity of the current cost function J in Eq. 18 can be guaranteed when r is tuned to be larger than a certain value and the Hermitian matrix in the QP will be positive definite. This approach was previously used for a cost function with a penalty term on the control input for reducing the power consumption (Li and Belmont 2014a). The current controller, in addition to restricting consumed power, can also achieve a smaller slew rate without adding constraints on the slew rate, which can significantly increase computational costs. Nevertheless, it should be pointed out that a larger weight r on penalizing the slew rate can result in a larger loss in the energy extraction. For cases simulated here, a small r (r < < 1) is sufficient to guarantee the convexity of the cost function. With the smallest r, the impact of the term on energy extraction is negligible.

3.2 Quadratic Programming Formulation

We will cast the problem into a QP. The following notations will be used:

$$\begin{array}{@{}rcl@{}} U_{0} &:=& [\boldsymbol{u}_{0}; \boldsymbol{u}_{1}; \dots; \boldsymbol{u}_{N_{h}-1}] \\ W_{0} &:=& [\boldsymbol{w}_{0}; \boldsymbol{w}_{1}; \dots; \boldsymbol{w}_{N_{h}-1}] \end{array} $$
(19)

which represent the series of inputs u and w at time instants k = 0, 1, … , Nh − 1, where we recall that u and w are column vectors denoting the machinery forces and the wave-exciting forces on all of the WECs, as defined in Eqs. 11a and 11b. The optimization problem is composed of the cost function (18) and constraints (17a) and (17b) with the dynamics in Eqs. 13a, 13b, and 13c satisfied.

To form the QP, we propagate the state equation (13a) and use (13b) to obtain \(\hat {y}(k+i|k)\), which denotes the state yk+i estimated at time k and stacks the output states to form the vector \(Y_{0}^{N_{h}-1} := \left [\hat {y}(k|k),\right .{\kern -4.9pt}\)\(\left .\hat {y}(k + 1|k), \dots , \hat {y}(k+N_{h}-1|k)\right ]^{T} \). \({Y}_{0}^{N_{h}-1}\) can then be expressed in a matrix form as follows:

$$ {Y}_{0}^{N_{h}-1} = S_{x} x_{k} + S_{u} (U_{0} + W_{0}) $$
(20)

where

$$\begin{array}{@{}rcl@{}} S_{x} &=& \left[\begin{array}{l} C; CA; CA^{2}; \dots; CA^{N_{h}-1} \end{array}\right] \\ S_{u} &=& \left[\begin{array}{ccccccc} 0 & & & & \\ CB & 0 & & & \\ CAB & CB & {\ddots} & & \\ {\vdots} & {\vdots} & {\ddots} & 0 & \\ CA^{N_{h}-2}B & \quad CA^{N_{h}-3}B &\quad {\dots} & CB & 0\\ \end{array}\right] \end{array} $$
(21)

In a similar manner, we can express the vector of states \(\hat {z}(k+i|k)\), i = 0, 1, … , Nh − 1, denoted by \(Z_{0}^{N_{h}-1}\) as follows:

$$ {Z}_{0}^{N_{h}-1} = S_{x,z} x_{k} + S_{u,z} (U_{0} + W_{0}) $$
(22)

where we substitute Cz for C in Eq. 21 to obtain Sx, z and Su, z. In matrix form, the slew input vector ΔU := \( {[{\Delta } \boldsymbol {u}_{0}; {\Delta } \boldsymbol {u}_{1}; {\Delta } \boldsymbol {u}_{2}; \dots ; {\Delta } \boldsymbol {u}_{N_{h}-1}]}\) can be written as follows:

$$ {\Delta} U = T_{\Delta} U_{0} - g_{u} $$
(23)

where

$$\begin{array}{@{}rcl@{}} T_{\Delta} &=& \left[\begin{array}{cccccc} 1 & & & & & \\ & {\ddots} & & & & \\ 0 & & 1 & & & \\ -1 & 0 & & 1 & & \\ & {\ddots} & {\ddots} & & {\ddots} & \\ & & -1 & 0 & & 1 \end{array}\right]_{NN_h\times NN_h} \\ &&~~~~~~~~~~~~~~~~~~~~~\underbrace{~~~~~~~~~~~~~}\\ g_u &=& \left[\begin{array}{ll} \boldsymbol{u}_{-1}; 0 ; \dots; 0\end{array}\right]^{~~~~~~~~N}_{NN_h\times 1} \end{array} $$
(24)

with u− 1 being the control input applied to the system currently and u− 1 = 0 initially. In the MPC, u− 1is the input obtained from the previous receding-horizon computation.

The cost function J in Eq. 18 can then be written in a compact form:

$$ J = {{U}_{0}^{T}} {Y}_{0}^{N-1} + (T_{\Delta} U_{0} - g_{u})^{T} R (T_{\Delta} U_{0} - g_{u}) $$
(25)

where \(R = r\times \mathcal {I}_{(NN_{h})}\) with \(\mathcal {I}\) being the identity matrix. Substituting Eqs. 20 and 23 in Eq. 25 and neglecting the constant term, we can write J in a quadratic form as follows:

$$ J = \frac{1}{2} {{U}_{0}^{T}} H U_{0} + f^{T} U_{0} $$
(26)

where

$$\begin{array}{@{}rcl@{}} H &:=& S_{u} + {{S}_{u}^{T}} + 2 S_{R} \end{array} $$
(27a)
$$\begin{array}{@{}rcl@{}} f &:=& S_{x} x_{k} + S_{u} W_{0} - 2 S_{g} \end{array} $$
(27b)

with SR := (TΔ)TRTΔ and Sg = (TΔ)TRgu.

It can be seen that without penalizing the slew rate, the cost function will have a corresponding Hessian matrix \(H_{0} = S_{u} + {{S}_{u}^{T}}\) where Su in Eq. 21 has zero diagonal elements, which may lead to an indefinite H0, and hence a nonconvex problem. The addition of SR, aside from controlling the slew rate, adds positive values on the diagonal of the matrix H per Eq. 27a. By tuning r so that the minimal eigenvalue of H is larger than 0, we can have a positive definite H, and hence a convex J.

The constraints (17a) and (17b) can be written in a component-wise inequality. Thus,

$$ A_{u} U_{0} \leq b_{u} $$
(28)

where it can be shown, with the use of Eq. 22, that

$$ A_{u} = \left[\begin{array}{c} I \\ -I \\ S_{u,z} \\ -S_{u,z} \end{array}\right] \text{,} \quad b_{u} = \left[\begin{array}{ccc} U_{\max} \\ U_{\max} \\ Z_{\max}-S_{x,z}x_{k}-S_{u,z}W_{0} \\ Z_{\max}+S_{x,z}x_{k}+S_{u,z}W_{0} \end{array}\right] \vspace{2mm} $$
(29)

with \({U_{\max } = f_{m,\max } \times \underbrace {[1, \dots , 1]}_{NN_{h}}}^{T}\) and \({Z_{\max } = \zeta _{3, \max } \times \underbrace {[1, \dots , 1]}_{NN_{h}}}^{T}\).

In summary, the QP with the cost function (26) subject to the constraints (28) can be written as follows:

$$\begin{array}{@{}rcl@{}} \min\limits_{U_{0}} \quad J &=& \frac{1}{2} {U_{0}^{T}} H U_{0} + f^{T} U_{0} \end{array} $$
(30a)
$$\begin{array}{@{}rcl@{}} \text{subject to} && A_{u} U_{0} \leq b_{u} \end{array} $$
(30b)

3.3 MPC Scheme—Implementation

The MPC scheme as presented is implemented as follows: at time instant k, with the knowledge of estimated states and the predicted wave profile, the QP in Eqs. 30a and 30b is solved, and a sequence of optimal control inputs \({U}_{0}^{*} = \arg \min (J)\) is generated; the first set of the control inputs in the sequence is applied; the system dynamics is then moved forward to the next time step, and the optimization procedure is repeated. In this paper, we will assume the knowledge of a certain future period of the incoming waves is available.

4 Results of Simulations

We applied the MPC formulated in Section 3 to an array of the dual coaxial-cylinder WEC (Son et al. 2016). A nonlinear MPC (NMPC) was developed and used by these authors for the single WEC, where the PTO damping function was used as the optimizer. The performance of the current formulation of MPC on a single WEC has been compared to that of the NMPC (Zhong and Yeung 2017). It was shown that by tuning the penalty weight r, the current MPC strategy can achieve a better performance in both regular and irregular waves in terms of its ability to broaden bandwidth of the capture width, while simultaneously saves computational time and power because of the convex formulation of the optimization problem. In this work, results for two cylinders will be presented in head seas and in beam seas for both regular waves and irregular waves. The performance of the two-body array is compared with that obtained for a single cylinder. It is common to define a q factor as follows:

$$ q = \frac{P_{u}}{NP_{u,s}} $$
(31)

where Pu is the useful power obtained by multiple absorbers, Pu, s is the power absorbed by a single or isolated absorber, N being the number of devices.

For comparison, we will also present results of the WEC using a passive controller, i.e., without considering constraints, where each WEC was equipped with a simple linear damper of nonnegative damping coefficient, Bg ≥ 0. The PTO force in time domain can be obtained by the following:

$$ {{f}_{g}^{j}}(t) = -{{B}_{g}^{j}} {\dot{\zeta}}_{3}^{j}(t) $$
(32)

As in Falnes (2002), the optimal linear damping of the j th cylinder in regular waves can be obtained by the following:

$$ {{B}_{g}^{j}}(\sigma) = \sqrt{\left( {\lambda}_{33}^{j}(\sigma)+\lambda_{\text{vis}})^{2} + (\sigma\cdot(m_{j} + {\mu}_{33}^{j}(\sigma))-\frac{K_{j}}{\sigma}\right)^{2}} $$
(33)

where λ33 and μ33 are hydrodynamic coefficients for the j th cylinder in isolation. For irregular waves, Bg will be tuned to correspond to the peak frequency of the wave spectrum.

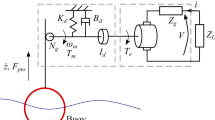
A dual coaxial-cylinder WEC, as shown in Fig. 2, was developed (Son and Yeung 2017). The (outer) cylinder or floater has a radius of 0.254 m and a draft of 0.635 m, and the WEC device has the total mass of 103.63 kg (including the added mass), and hydrostatic stiffness coefficient of 1285.6 N/m. Water depth is 1.5 m. Additionally, the equivalent linear-viscous damping factor λvis = 1.7λ33 = 9.68 N ⋅s/m was obtained from experiments (Son et al. 2016). The hydrodynamic coefficients for the single device with the coaxial geometry were obtained by an in-house code (Chau and Yeung 2012). A fifth-order state-space model was used to approximate its radiation subsystem to achieve an accuracy of 0.999. This impulse response Kr(t) and its fifth-order approximation used is shown in Fig. 4a, as well as the damping coefficient λ33 plotted versus the dimensional wave frequency σ.

Fig. 2
figure 2

Schematic of the dual coaxial-cylinder WEC system (Son and Yeung 2017), with “The Berkeley Wedge” bottom geometry

Full size image

For the array, we assumed two identical devices placed in an arrangement as shown in Fig. 3. To ensure the reasonable validity of the point-absorber theory, the center-to-center spacing L is set to L = 10a with a being the radius of the (outer) cylinder. Regarding the modeling of wave radiation forces, as \({\lambda }_{33}^{jj} = \lambda _{33}\), the radiation subsystem for \({K}_{r}^{jj}\) can be the same as the one for the isolated cylinder. A tenth-order state-space model was used to approximate the radiation subsystem for \({K}_{r}^{jl}\) (l ≠ j) representing the force induced by interacting waves, where the damping coefficients were computed based on Eq. 7. The impulse response \(K_{r}^{jl}(t)\) and the corresponding damping coefficient \({\lambda }_{33}^{jl}\) are shown in Fig. 4b.

Fig. 3
figure 3

Plan view of the configuration of two identical WEC devices, separated by a distance of L, with incident waves making an angle β

Full size image
Fig. 4
figure 4

Impulse response of the radiation subsystems and the damping coefficient with respect to wave frequency

Full size image

As for the MPC controller, the oscillation amplitude of the absorber is constrained to be no larger than the maximal response amplitude obtained by the NMPC (Son and Yeung 2017): ζ3,max = 5.1A0. In addition, the maximal machinery force is computed by fm,max = Bg,maxζ3,maxσ, where σ is the angular frequency of incident waves and the maximal damping Bg,max = 150 N⋅s/m (Son and Yeung 2017). We set the penalty weight r to be \(r = \overline {r}/{{T}_{w}^{2}}\), where the scaling factor \({{T}_{w}^{2}}\) with Tw being the period of incoming waves was introduced to reduce the effect of the time interval on the penalty of the slew rate; and \(\overline {r}\) was chosen such that the cost function (18) becomes convex. The quadprog solver in MATLAB was used to solve the QP for the MPC.

4.1 Illustrative Results in a Regular Wave Environment

Under linear theory, the wave-exciting force induced by a regular wave of frequency σ on the cylinder j can be obtained by the following:

$$ {{f}_{e}^{j}}(t) = A_{0}\Re \left\{{{X}_{3}^{j}}(\sigma)\mathrm{e}^{-\mathrm{i}\sigma t}\right\} $$
(34)

where A0 is the amplitude of an incoming wave, and \({{X}_{3}^{j}}\) obtained by Eq. 8 is the complex amplitude of the wave-exciting force on the j th cylinder induced by a unit-amplitude wave of frequency σ. For simulations, A0 = 0.0254 m. For the discrete-time model in Eqs. 13a and 13b, the wave-exiciting force on cylinder j is obtained by the following:

$$ {{w}_{k}^{j}} = A_{0}\Re \left\{{{X}_{3}^{j}}(\sigma)\mathrm{e}^{-\mathrm{i}\sigma kT_{s}}\right\} $$
(35)

where \({{w}_{k}^{j}}\) denotes the \({{f}_{e}^{j}}\) at time instant k with k = 0, 1, … , Nh − 1. Simulations were carried out for 20Tw with 80 time steps per wave period.

The nondimensional capture width \(\overline {C}_{w}\) and the maximal response amplitude operator (RAO) of absorbers in the array, plotted over the nondimensional frequency \(\overline {\sigma }\), are shown in Figs. 5 and 6 and compared with those obtained by the (unconstrained) passive control. The parameters were defined by as follows:

$$\begin{array}{@{}rcl@{}} \overline{C}_{w} &=& \frac{C_{w}}{2a} = \frac{1}{2a} \frac{\overline{P_{u}(t)}/N}{P_{\text{wave}}} \end{array} $$
(36a)
$$\begin{array}{@{}rcl@{}} \text{RAO}_{\max} &=& \max\left( \frac{{\zeta_{3}^{1}}}{A_{0}}, \frac{{\zeta_{3}^{2}}}{A_{0}}, \dots, \frac{{\zeta_{3}^{N}}}{A_{0}}\right) \end{array} $$
(36b)
$$\begin{array}{@{}rcl@{}} \overline{\sigma} &=& \sigma \sqrt{\frac{a}{g}} \end{array} $$
(36c)

with g being the gravitational acceleration, Pwave the wave power, and \({\overline {P_{u}(t)} = \frac {1}{T} {\int }_{T_{0}}^{T_{0}+T} f_{m}(t)\dot {\zeta }_{3}(t) \text {d}t}\), indicating the energy extracted by the WEC array, which is then averaged over the N bodies. For a regular wave of amplitude A0 and group velocity vg, the wave power can be obtained by \({P_{\text {wave}} = \frac {1}{2}\rho g {A_{0}^{2}} v_{g}}\). Results are shown for different values of penalty weight r with the minimal value \(r_{\min } = 10^{-1.3}/{T_{w}^{2}}\) for guaranteeing the convexity of the cost function; also presented are the result for an array of two with unconstrained MPC and that of a single WEC controlled by the current MPC for reference.

Fig. 5
figure 5

Nondimensional capture width of WEC(s) in head seas (β = 0°) of regular waves

Full size image
Fig. 6
figure 6

Maximal RAO of WEC(s) in head seas (β = 0°) of regular waves

Full size image

Several observations can be made. Constraints largely affect the performance of the WECs at low frequency where large motion is needed to generate the optimal power. At higher frequencies, with the minimal penalty on the slew rate of the control input, the constrained MPC is able to produce approximately the same amount of the power as the unconstrained MPC. With an increase of the penalty weight r, less power was generated to have a milder changing rate of the input, and a smaller RAO was achieved. In general, the MPC outperformed the passive controller in terms of increasing the energy absorption, especially at frequencies far from the resonance frequency \(\overline {\sigma } = 0.5668\). However, the current MPC approach taking the machinery force as the control input will require power to motor the WEC system, i.e., the so-called “reactive power,” while the passive control of the damping will not consume power. Figure 7 shows the ratio of the power flowing from the PTO units to the absorbers (reactive power \(\overline {P}_{\text {react}}\)) to the power flowing from the absorbers to the PTO units (so-called “active power” \(\overline {P}_{\text {act}}\)). The net power is the useful power, given by \(\overline {P}_{u} = \overline {P}_{\text {act}}-\overline {P}_{\text {react}}\). It can be seen that less reactive power is required with larger r. Further, the closer the frequency is to the resonance frequency, the smaller the reactive power is; at the resonance frequency, no reactive power is needed. Similar results were found for a single WEC (Zhong and Yeung 2017).

Fig. 7
figure 7

The ratio of the reactive power to the power flowing from the absorbers to the PTO units (so-called “active power”) for a two-WEC array in head seas (β = 0°)

Full size image

As shown in Fig. 5, at resonance frequency, all of the controllers for the WEC array achieve a similar amount of energy production which, on average, is smaller than the one generated by an isolated WEC. This is attributed to the destructive wave effect. In Fig. 8, the interaction factor q defined in Eq. 31 was shown for WEC arrays controlled by the constrained and the unconstrained MPC, and the complex-conjugate (CC) control in Evans (1979) and Falnes (1980) for comparison. It can be seen that values of the factor q of different control strategies follow a similar trend; at resonance frequency, the cylinders in beam seas (β = 90°) experienced constructive wave effects with q > 1 while the ones in head seas (β = 0°) experiences the destructive effects. This suggests that the MPC is able to achieve the optimal condition of the array with constraints taken into account. Furthermore, it appears the effect of interacting waves on the energy-capture ability of a WEC array compared to isolated WECs, is indepedent of the controller, with the assumption that the devices are weak scatterers. Hence, it is possible to predict the energy captured by a WEC array with a certain controller by obtaining the energy produced by a single isolated WEC with the same controller, and also the q factor from CC control, which can be easily computed. This way will be more efficient than running simulations for the whole array, and will be beneficial for the preliminary design of a large WEC array. It is also noticed that adding constraints will reduce wave effects as it restricts the heaving motion of devices which radiates waves.

Fig. 8
figure 8

Interaction factor for an array of two WECs in head seas and beam seas of regular waves

Full size image

Time histories of the two-body array are shown in the Fig. 9 for waves of period Tw = 1.8 s around the resonance frequency. It can be seen that the phases of the heaving velocity of the devices match that of corresponding wave-exciting forces, a similar result to the case of a single cylinder. However, it was pointed out (Thomas and Evans 1981) that, the phase matching at the optimal condition was not obtained for an array with k0L < 3 where L is the spacing between devices. Here, in order to reduce the effect of scattering waves so that the point-absorber approximation stays valid, we choose a relatively large spacing L = 10a and have k0L = 3.13. We believe the phase difference between the heaving velocity and the wave force will be more significant with the decrease in spacing or an increase in the number of devices.

Fig. 9
figure 9

Time histories of \(\dot {\zeta }_{3}\) (blue), ζ3 (black, dash-dotted), and fe (red, dashed) on the left, and fm (gray, dash-dotted) and fe on the right, for the two devices in regular waves of period Tw = 1.8s (\(\overline {\sigma } = 0.56\)). Constraints on ζ3 are shown by dotted lines, while the constraints on Fg are not active in this case

Full size image

4.2 Performance in Irregular Waves

The proposed MPC was then applied to study the performance of a WEC in irregular wave conditions. A modified Pierson-Moskowitz spectrum for fully developed seas was used to construct the irregular wave profile:

$$\begin{array}{@{}rcl@{}} S(\sigma) &=& {H_{s}^{2}} T_{1} \frac{0.11}{2\pi} \left( \frac{\sigma T_{1}}{2\uppi}\right)^{-5} \exp \left[ -0.44\left( \frac{\sigma T_{1}}{2\uppi}\right)^{-4}\right] \end{array} $$
(37a)
$$\begin{array}{@{}rcl@{}} T_{1} &=& 0.7713 T_{p} \end{array} $$
(37b)
$$\begin{array}{@{}rcl@{}} A(\sigma_{j}) &=& \sqrt{2S(\sigma_{j}){\Delta}\sigma} \end{array} $$
(37c)
$$\begin{array}{@{}rcl@{}} \eta(t) &=& \sum\limits_{j = 1}^{N} A(\sigma_{j})\sin(\sigma_{j} t+\varepsilon_{j}) \end{array} $$
(37d)
$$\begin{array}{@{}rcl@{}} f_{e}(t) &=& \sum\limits_{j = 1}^{N} |X_{3}(\sigma_{j})| A(\sigma_{j}) \sin(\sigma_{j} t+ \delta_{j} + \varepsilon_{j}) \end{array} $$
(37e)

where Hs, Tp, Aj, and δj are the significant wave height, peak period, wave amplitude, and phase angle of the wave-exciting force the j th-component, respectively, and εj is a random phase angle of the wave components. The random phase angles are uniformly distributed between 0 and 2π and constant with time. The range of angular frequencies used in the construction of Eqs. 37a, 37b, 37c, 37d, and 37e was between 0.1 and 8.75 rad/s spaced at 0.05 rad/s. The simulation runs for Hs = 7.62 cm (3.0 in) and varying Tp, carried out for 1 000 peak-wave periods with 40 time steps per peak period and the time horizon Th = 2Tp. In this application, the RAO is constrained to be half of the significant wave height, i.e., ζ3,max = Hs/2, which was the maximal RAO used in the NMPC work (Son and Yeung 2017). The maximal machinery force is computed in the same way as described in Section 4.1 with σ = 2π/Tp. And the penalty weight \(r = 10^{-1.1}/{T_{p}^{2}}\) is used.

Results of the averaged useful power absorbed by the array in head seas (β = 0°) and beam seas (β = 90°) are shown in Fig. 10 and compared with the single-device case. The ratio of the reactive power to the “active” power is shown in Fig. 11. For both the two-device and single-device cases, more useful power is extracted when peak wave conditions are closer to the resonance frequency Tp = 1.784 s. It is observed that in general a smaller reactive power ratio is required for WECs in irregular waves than those in regular waves. This is expected as the composition of waves of different frequencies reduces the efforts required from the PTO unit to drive the absorber in phase with waves, compared to the case where the frequency of the monochromatic waves is substantially different from the resonance frequency. This fact is favorable for applications in real-sea environments. q factor is plotted over the nondimensional frequency for the peak waves in Fig. 12, and also compared with that obtained by using CC control. It is interesting to note that in irregular waves, the interaction factor of the WEC array does not appear to follow the trend of q obtained in the regular waves. In addition, with effects coming from waves of various frequencies, both the constructive and the destructive effects of radiating waves were much reduced.

Fig. 10
figure 10

Averaged useful power in irregular waves

Full size image
Fig. 11
figure 11

The ratio of reactive power to active power in irregular waves

Full size image
Fig. 12
figure 12

Interaction factor q for an array of two WECs in head seas and beam seas of irregular waves

Full size image

5 Conclusions

We have extended the MPC for a single WEC (Zhong and Yeung 2017), for which a convex QP was formed for the optimization problem, and applied it to an array of heaving point absorbers so that an optimal control law can be obtained to maximize the global performance of the array with constraints on both the motion of devices and machinery forces satisfied. A penalty term introduced in the cost function of the MPC can ensure the convexity of the problem and penalize the slew rates of the machinery forces so that the reactive power required by the MPC can be adjusted. The wave-interaction effects among the array was taken into account in the dynamic model by adopting the point-absorber approximation.

In general, the current MPC outperformed the passive control strategy in terms of a broadening of the capture-width bandwidth. By tuning the penalty weight r, the reactive power required by the system can be adjusted. The convex formulation allows efficient computations for an array of large number of elements, though we applied the method on only two bodies for demonstration. In regular waves, the q factor obtained by the current MPC follows the same trend of the one obtained by complex-conjugate control. This suggests that the current MPC provides a control law that optimizes the global performance of the array with physical constraints accommodated simultaneously. It should be pointed out that adding constraints on the motion reduces wave-interaction effects as it reduces the radiating waves. At resonance frequency, phase matching between the oscillation velocity and the wave-exciting force was obtained by both cylinders in the array. However, this may not be the case for arrays with less spacing distance or more elements, for which the effect of scattering waves would no longer be negligible. In irregular waves, the wave-interaction effects seems not be predictable by using the results obtained in the regular waves. With effects coming from waves of various frequencies, the q factor of the array in irregular waves of a certain (peak) frequency differs from the one obtained in regular waves of the same frequency. It is also because of the presence of multiple frequencies of wave that the reactive power required by the current MPC in irregular waves is in general lower than that in regular waves.

For future study, a more accurate model for considering wave-interaction effects (Zhong and Yeung 2016) will be adopted in the dynamics model. This theory provides an efficient method to obtain hydrodynamic properties of an arbitrary array of devices. Effects of the scattering waves on the performance of the WEC array and the control law can then be investigated and understood. We will also be looking into the energy-capture capability of arrays with different configurations under control.