Skip to main content
SpringerLink
Log in

Strong convergence of a self-adaptive method for the split feasibility problem in Banach spaces

  • Published:
Journal of Fixed Point Theory and Applications Aims and scope Submit manuscript

Abstract

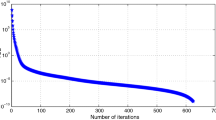
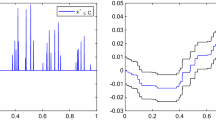
In signal processing and image reconstruction, the split feasibility problem (SFP) has been now investigated extensively because of its applications. A classical way to solve the SFP is to use Byrne’s CQ-algorithm. However, this method requires the computation of the norm of the bounded linear operator or the matrix norm in a finite-dimensional space. In this work, we aim to propose an iterative scheme for solving the SFP in the framework of Banach spaces. We also introduce a new way to select the step-size which ensures the convergence of the sequences generated by our scheme. We finally provide examples including its numerical experiments to illustrate the convergence behavior. The main results are new and complements many recent results in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitzian-type Mappings with Applications, Topological Fixed Point Theory and Its Applications, vol. 6. Springer, New York (2009)

  2. Alber, Y.I.: Metric and generalized projections in Banach spaces: properties and applications. In: Kartsatos, A.G. (ed.) Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, pp. 15–20. Dekker, New York (1996)

    Google Scholar 

  3. Alber, Y.I., Butnariu, D.: Convergence of Bregman projection methods for solving consistent convex feasibility problems in reflexive Banach spaces. J. Optim. Theory Appl. 92, 33–61 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  4. Aleyner, A., Reich, S.: Block-iterative algorithms for solving convex feasibility problems in Hilbert and in Banach spaces. J. Math. Anal. Appl. 343, 427–435 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Alsulami, S.M., Takahashi, W.: Iterative methods for the split feasibility problem in Banach spaces. J. Convex Anal. 16, 585–596 (2015)

    MathSciNet  MATH  Google Scholar 

  6. Bauschke, H.H., Borwein, J.M., Combettes, P.L.: Bregman monotone optimization algorithms. SIAM J. Control Optim. 42, 596–636 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bonesky, T., Kazimierski, K.S., Maass, P., Schöpfer, F., Schuster, T.: Minimization of Tikhonov functionals in Banach spaces. Abstr. Appl. Anal. 2008, 192679 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Brègman, L.M.: A relaxation method of finding a common point of convex sets and its applications to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7, 200–217 (1967)

    Article  MathSciNet  Google Scholar 

  9. Butnariu, D., Iusem, A.N.: Totally Convex Functions for Fixed Points Computation and Infinite Dimensional Optimization, vol. 40. Kluwer, Dordrecht (2000)

    MATH  Google Scholar 

  10. Butnariu, D., Iusem, A.N., Resmerita, E.: Total convexity for powers of the norm in uniformly convex Banach spaces. J. Convex Anal. 7, 319–334 (2000)

    MathSciNet  MATH  Google Scholar 

  11. Butnariu, D., Kassay, G.: A proximal-projection method for finding zeros of set-valued operators. SIAM J. Control Optim. 47, 2096–2136 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Byrne, C.: Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 18, 441–453 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)

    MathSciNet  MATH  Google Scholar 

  14. Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Lecture Notes in Mathematics, vol. 2057. Springer, Berlin, ISBN 978-3-642-30900-7 (2012)

  15. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 8, 221–239 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  16. Censor, Y., Lent, A.: An iterative row-action method for interval convex programming. J. Optim. Theory Appl. 34, 321–353 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  17. Chidume, C.E.: Geometric properties of Banach spaces and nonlinear iterations. Lecture Notes in Mathematics, vol. 1965, XVII. Springer, Berlin, ISBN 978-1-84882-189-7 (2009)

  18. Cioranescu, I.: Geometry of Banach spaces, Duality Mappings and Nonlinear Problems, vol. 62. Kluwer, Dordrecht (1990)

    Book  MATH  Google Scholar 

  19. Ekeland, I., Temam, R.: Convex Analysis and Variational Problems. North-Holland, Amsterdam (1976)

    MATH  Google Scholar 

  20. Kohsaka, F., Takahashi, W.: Proximal point algorithms with Bregman functions in Banach spaces. J. Nonlinear Convex Anal. 6, 505–523 (2005)

    MathSciNet  MATH  Google Scholar 

  21. Kuo, L.-W., Sahu, D.R.: Bregman distance and strong convergence of proximal-type algorithms. Abstr. Appl. Anal. 2013, 590519 (2013)

    Article  MathSciNet  Google Scholar 

  22. López, G., Martin-Márquez, V., Wang, F., Xu, H.K.: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28, 085004 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  23. Maingé, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 16, 899–912 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  24. Masad, E., Reich, S.: A note on the multiple-set split convex feasibility problem in Hilbert space. J. Nonlinear Convex Anal. 8, 367–371 (2007)

    MathSciNet  MATH  Google Scholar 

  25. Moudafi, A.: Split monotone variational inclusions. J. Optim. Theory Appl. 150, 275–283 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Moudafi, A., Thakur, B.S.: Solving proximal split feasibility problems without prior knowledge of operator norms. Optim. Lett. 8, 2099–2110 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  27. Moudafi, A.: A relaxed alternating CQ-algorithm for convex feasibility problems. Nonlinear Anal. 79, 117–121 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Moudafi, A.: Alternating CQ-algorithm for convex feasibility and split fixed-point problems. J. Nonlinear Convex Anal. 15, 809–818 (2014)

    MathSciNet  MATH  Google Scholar 

  29. Schöpfer, F., Schuster, T., Louis, A.K.: An iterative regularization method for the solution of the split feasibility problem in Banach spaces. Inverse Probl. 24, 055008 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Shehu, Y.: Iterative methods for split feasibility problems in certain Banach spaces. J. Nonlinear Convex Anal. 16, 2315–2364 (2015)

    MathSciNet  MATH  Google Scholar 

  31. Shehu, Y., Iyiola, O.S., Enyi, C.D.: An iterative algorithm for solving split feasibility problems and fixed point problems in Banach spaces. Numer. Algorithms 72, 835–864 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  32. Takahashi, W.: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama (2000)

    MATH  Google Scholar 

  33. Wang, F.: A new algorithm for solving the multiple-sets split feasibility problem in certain Banach spaces. Numer. Funct. Anal. Optim. 35, 99–110 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  34. Xu, H.K.: Inequalities in Banach spaces with applications. Nonlinear Anal. 16, 1127–1138 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  35. Xu, H.K.: Another control conditions in an iterative method for nonexpansive mappings. Bull. Aust. Math. Soc. 65, 109–113 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  36. Xu, H.K.: Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces. Inverse Probl. 26, 105018 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Yao, Y., Postolache, M., Liou, Y.C.: Strong convergence of a self-adaptive method for the split feasibility problem. Fixed Point Theory Appl. 2013 (2013). https://doi.org/10.1186/1687-1812-2013-201

  38. Zhou, H., Wang, P.: Some remarks on the paper “Strong convergence of a self-adaptive method for the split feasibility problem”. Numer. Algorithms 70, 333–339 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research was supported by the Thailand Research Fund and the Commission on Higher Education under Grant MRG5980248. S. Suantai would like to thank Chiang Mai University. The research was carried out when the second author was an Alexander von Humboldt Postdoctoral Fellow at the Institute of Mathematics, University of Wurzburg, Germany. He is grateful to the Alexander von Humboldt Foundation, Bonn, for the fellowship and the Institute of Mathematics, Julius Maximilian University of Wurzburg, Germany, for the hospitality and facilities.

Author information

Authors and Affiliations

  1. Center of Excellence in Mathematics and Applied Mathematics, Department of Mathematics, Faculty of Science, Chiang Mai University, Chiang Mai, 50200, Thailand

    Suthep Suantai

  2. Department of Mathematics, Faculty of Science, University of Nigeria, Nsukka, Nigeria

    Yekini Shehu

  3. School of Science, University of Phayao, Phayao, 56000, Thailand

    Prasit Cholamjiak

  4. Department of Mathematical Sciences, University of Wisconsin-Milwaukee, Milwaukee, WI, USA

    Olaniyi S. Iyiola

Authors
  1. Suthep Suantai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yekini Shehu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Prasit Cholamjiak
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Olaniyi S. Iyiola
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Prasit Cholamjiak.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Suantai, S., Shehu, Y., Cholamjiak, P. et al. Strong convergence of a self-adaptive method for the split feasibility problem in Banach spaces. J. Fixed Point Theory Appl. 20, 68 (2018). https://doi.org/10.1007/s11784-018-0549-y

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s11784-018-0549-y

Keywords

Mathematics Subject Classification

Search

Navigation