Skip to main content
SpringerLink
Log in

Risk assessment model of tunnel water inrush based on improved attribute mathematical theory

基于改进属性数学理论的隧道突涌水评估模型

  • Published:
Journal of Central South University Aims and scope Submit manuscript

Abstract

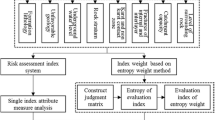
Tunnel water inrush is one of the common geological disasters in the underground engineering construction. In order to effectively evaluate and control the occurrence of water inrush, the risk assessment model of tunnel water inrush was proposed based on improved attribute mathematical theory. The trigonometric functions were adopted to optimize the attribute mathematical theory, avoiding the influence of mutation points and linear variation zones in traditional linear measurement functions on the accuracy of the model. Based on comprehensive analysis of various factors, five parameters were selected as the evaluation indicators for the model, including tunnel head pressure, permeability coefficient of surrounding rock, crushing degree of surrounding rock, relative angle of joint plane and tunnel section size, under the principle of dimension rationality, independence, directness and quantification. The indicator classifications were determined. The links among measured data were analyzed in detail, and the objective weight of each indicator was determined by using similar weight method. Thereby the tunnel water inrush risk assessment model is established and applied in four target segments of two different tunnels in engineering. The evaluation results and the actual excavation data agree well, which indicates that the model is of high credibility and feasibility.

摘要

隧道突涌水是地下工程建设中常见的地质灾害之一。 为了评估并控制突涌水的发生, 建立基于改进属性数学理论的隧道突涌水评估模型。 利用三角函数曲线对属性数学理论进行优化, 避免传统的线性预测函数的突变点以及线性变化区域对模型精度的影响。 基于对多种因素的综合分析, 选取 5 个参数作为模型评估指标, 即隧道水头压力、 围岩渗透系数、 围岩破碎程度、 节理面的相对角度以及隧道断面面积, 同时, 满足评估指标集的维度合理性、 独立性、 直接性以及可量化的原则。 详细分析了测量数据之间的关联, 并利用相似权重法确定了每项指标的目标权重, 进而建立了隧道突涌水风险评估模型。 将该方法运用到 2 条不同隧道的 4 个标段, 评价结果与实际开挖情况对比表明, 二者吻合良好, 说明模型具有较高的精度。

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. LI C P, LI J J, LI Z X, HOU D Y. Establishment of spatiotemporal dynamic model for water inrush spreading processes in underground mining operations [J]. Safety Science, 2013, 55: 45–52.

    Article  Google Scholar 

  2. SHEN X M, LIU P L, WANG J F. Evaluation of Water-inrush risks of karst tunnel with analytic hierarchy process [J]. Journal of Railway Engineering Society, 2010, 12: 56–63. (in Chinese)

    Google Scholar 

  3. DU Y C, HAN X R, LI Z L. Professional evaluating system for karst tunnel gushing based on AHP and its application [J]. Carsologica Sinica, 2009, 3: 281–287. (in Chinese)

    Google Scholar 

  4. YANG T H, TANG C A, TAN Z H, ZHU W C. State of the art of inrush models in rock mass failure and developing trend for prediction and forecast of groundwater inrush [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 2: 268–277. (in Chinese)

    Google Scholar 

  5. MIAO C L, SUN L Y, YANG L. Evaluation method for coalmining-based cities ecosystem based on attribute mathematical model with Huainan City as an example [J]. Ecological Indicators, 2015, 48: 17–21.

    Article  Google Scholar 

  6. XU J S, LI Y X, YANG X L. Stability charts and reinforcement with piles in 3D nonhomogeneous and anisotropic soil slope [J]. Geomechanics and Engineering, 2018, 14(1): 71–81.

    Google Scholar 

  7. XU J S, PAN Q J, YANG X L, LI WT. Stability charts for rock slopes subjected to water drawdown based on the modified nonlinear Hoek-Brown failure criterion [J]. International Journal of Geomechanics, 2018, 18(1). DOI: 10.1061/(ASCE)GM.1943-5622.0001039.

    Google Scholar 

  8. YANG Z H, ZHANG R, XU J S, YANG X L. Engery analysis of rock plug thickness in karst tunnels based on non-associated flow rule and nonlinear failure criterion [J]. Journal of Central South University, 2017, 24(12): 2940–2950.

    Article  Google Scholar 

  9. TUNG F, LITTLE J. Improving scene attribute recognition using web-scale object detectors [J]. Computer Vision and Image Understanding, 2015, 138: 86–91.

    Article  Google Scholar 

  10. YEH Y C, SCHMEISER B W. VAMP1RE: A single criterion for rating and ranking confidence-interval procedures [J]. IIE Transactions (Institute of Industrial Engineers), 2015, 47(11): 1203–1216.

    Google Scholar 

  11. LI Z L, WANG X H, XIE L Z. Testing and applied research on grouting materials on karst tunnel water inrush [J]. Electronic Journal of Geotechnical Engineering, 2012, 17U: 2933–2942.

    Google Scholar 

  12. YANG X L, YAO C. Stability of tunnel roof in nonhomogeneous soils [J]. International Journal of Geomechanics, 2018, 18: 06018002. DOI: 10.1061/(ASCE)GM.1943-5622.0001104.

    Article  Google Scholar 

  13. YANG X L. Lower bound analytical solution for bearing capacity factor using modified Hoek–Brown failure criterion [J]. Canadian Geotechnical Journal, 2018, 55. DOI: https://doi.org/10.1139/cgj-2016-0694.

    Google Scholar 

  14. PENG J, LI X Y. Water-inrush mechanism during construction and determination of safety distance from the water source in a karst tunnel [J]. Electronic Journal of Geotechnical Engineering, 2015, 20(8): 2345–2354.

    Google Scholar 

  15. ZHANG M Q, HUANG H J, MIAO D H, TIAN S M. Study on and determination of water pressure of the karst tunnel [J]. Journal of Railway Engineering Society, 2008, 5: 53–58. (in Chinese)

    Google Scholar 

  16. RONG G, HOU D, LIU G, PENG J. Research of permeability distribution with burial depth in the fractured rock mass in valley slope [J]. International Journal of Earth Sciences and Engineering, 2013, 6(3): 442–446.

    Google Scholar 

  17. LU X B, ZHENG W, LIU Q J, ZHAN X H. A Method for Determining the Permeability Coefficient of Fractural Rock Based on the Percolation Model [J]. China Earthquake Engineering Journal, 2011(S1): 43–47.(in Chinese)

    Google Scholar 

  18. YANG X L, ZHANG R. Limit analysis of stability of twin shallow tunnels considering surface settlement [J]. KSCE Journal of Civil Engineering, 2018, 22. DOI: https://doi.org/10.1007/s12205-017-1398-8.

    Google Scholar 

  19. LI T Z, LI Y X, YANG X L. Rock burst prediction based on genetic algorithms and extreme learning machine [J]. Journal of Central South University, 2017, 24(9): 2105–2113.

    Article  Google Scholar 

  20. MUYA M S, HE B, WANG J T, LI G C. Simulation of stress distribution around tunnels and interaction between tunnels using an elasto-plastic model [J]. Journal of China University of Geosciences, 2007, 18(1): 90–94.

    Article  Google Scholar 

  21. YANG X L, ZHANG R. Collapse analysis of shallow tunnel subjected to seepage in layered soils considering joined effects of settlement and dilation [J]. Geomechanics and Engineering, 2017, 13(2): 217–235.

    Google Scholar 

  22. YANG X L, LI Z W, LIU Z A, XIAO H B. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media [J]. Journal of Central South University, 2017, 24(4): 957–966.

    Article  Google Scholar 

  23. WANG G B, YAN E C, YANG W D. Research on Development and Water Burst Mechanism of Karst in Wuchiba Tunnel [J]. Journal of Wuhan University of Technology, 2008, 8: 152–156. (in Chinese)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, Central South University, Changsha, 410075, China

    Xiao-li Yang  (杨小礼) & Sheng Zhang  (张胜)

Authors
  1. Xiao-li Yang  (杨小礼)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sheng Zhang  (张胜)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiao-li Yang  (杨小礼).

Additional information

Foundation item: Project(2013CB036004) supported by National Basic Research Program (973) of China; Project(51378510) supported by National Natural Science Foundation of China

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Xl., Zhang, S. Risk assessment model of tunnel water inrush based on improved attribute mathematical theory. J. Cent. South Univ. 25, 379–391 (2018). https://doi.org/10.1007/s11771-018-3744-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11771-018-3744-5

Key words

关键词

Search

Navigation