Abstract
The comparison of investments is a key research topic in mathematical finance. Financial derivatives are popular tools for economic investments. A common financial derivative is the so-called condor derivative. A new mathematical framework for the comparison of investments in condor derivatives is introduced in this manuscript. That model is based on the theory of stochastic orders. Namely, a new family of stochastic orders to approach such comparison problems is introduced. That family is analyzed in detail providing characterizations of the new orders, properties and connections with other stochastic orderings. Results which permit to compare condor derivatives, when the prices of the underlying assets follow Brownian movements, or geometric Brownian movements, are developed. Moreover, an analysis with the DOWJONES and EUROSTOXX indexes shows how to use the new stochastic orders to compare investments in condor derivatives based on those indexes. On the other hand, it is shown how well-known stochastic orders can be applied to compare investments in other financial derivatives, like future derivatives, bull call spreads, call options or long straddle derivatives.




Similar content being viewed by others
Notes
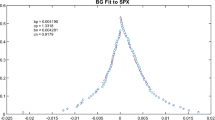
See the web addresses http://www.invertia.com/mercados/bolsa/indices/eurostoxx-50/historico-ib020stoxx50 and http://www.invertia.com/mercados/bolsa/indices/dow-jones/historico-ib016indu for DOWJONES and EUROSTOXX indexes, respectively.
References
Belzunce F, Martínez-Riquelme C, Mulero J (2016) An introduction to stochastic orders. Elsevier/Academic Press, Amsterdam
Bickel PJ, Lehmann EL (1976) Descriptive statistics for nonparametric models. III. Dispersion. Ann Stat 4:1139–1158
Billingsley P (1999) Convergence of probability measures. Wiley series in probability and statistics, 2nd edn. Wiley, New York
Birnbaum ZW (1948) On random variables with comparable peakedness. Ann Math Stat 19:76–81
Cohen G (2005) The bible of options strategies. Pearson Education Inc, Upper Saddle River
Dixit AK, Pindyck RS (1994) Investment under uncertainty. Princeton University Press, Princenton
Finner H, Roters M, Dickhaus T (2007) Characterizing density crossing points. Am Stat 61:28–33
Giovagnoli A, Wynn HP (1995) Multivariate dispersion orderings. Stat Probab Lett 22:325–332
Halmos PR (1950) Measure theory. D. Van Nostrand Company Inc, New York
Hull JC (2015) Options, futures and other derivatives. Pearson, Boston
Hunt P, Kennedy J (2004) Financial derivatives in theory and practice. Wiley series in probability and statistics. Wiley, Chichester
Jarrow RA, Chatterjea A (2013) An introduction to derivative securities, financial markets, and risk management. W.W. Norton & Co, New York
Klebaner FC (2012) Introduction to stochastic calculus with applications, 3rd edn. Imperial College Press, London
Kolb RW, Overdahl JA (2002) Financial derivatives, 3rd edn. Wiley, Upper Saddle River
López-Díaz M (2010) A stochastic order for random variables with applications. Aust NZ J Stat 52:1–16
Müller A (1997) Stochastic orders generated by integrals: a unified study. Adv Appl Probab 29:414–428
Müller A (1998) Another tale of two tails: on characterizations of comparative risk. J Risk Uncertain 16:187–197
Müller A, Stoyan D (2002) Comparison methods for stochastic models and risks. Wiley, Chichester
Shaked M, Shanthikumar JG (2007) Stochastic orders. Springer, New York
Tretyakov MV (2013) Introductory course on financial mathematics. Imperial College Press, London
Acknowledgements
The authors would like to thank the referees and the editor for their interesting comments and suggestions which have improved the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are indebted to the Spanish Ministry of Science and Innovation and to Principado de Asturias, since this research is financed by Grants MTM2013-45588-C3-1-P, MTM2015-63971-P, FC-15-GRUPIN14-101 and FC-15-GRUPIN14-142.
Appendix
Appendix
Proofs of mathematical results are included in this appendix.
Proof of Lemma 1
Observe that \(f_{p_2,p_2,p_3,p_4,k}= f_{p_2,p_2,p_3,p_4,0}+k\) for any \(p_1,p_2,p_3,p_4,k \in \mathbb {R}\) with \(p_1<p_2<p_3 <p_4\), which leads to the result. Note that \(\, \mathcal{F}_0^{p_2,p_3} \,\subset \, \mathcal{F}^{p_2,p_3} \,\). \(\square \)
Proof of Lemma 2
Let us see (i). Consider \(\{f_{p_2-1/n,p_2,p_3,p_4,k}\}_n \subset \, \mathcal{F}^{p_2,p_3} \,\). Condition \(X \, \preceq _{con}^{p_2,p_3} \,Y\) implies \(E(f_{p_2-1/n,p_2,p_3,p_4,k}(X)) \le E(f_{p_2-1/n,p_2,p_3,p_4,k}(Y))\) for all \(n \in \mathbb {N}.\) Note that for any \(x \in \mathbb {R}\) we have that \(\lim _n f_{p_2-1/n,p_2,p_3,p_4,k}(x)=f_{p_2,p_2,p_3,p_4,k}(x)\), and the above sequence of mappings is uniformly bounded. The dominated convergence theorem leads to (i). In a similar way, it is possible to prove (ii) and (iii). \(\square \)
Proof of Proposition 1
Let us suppose that \(X \, \preceq _{con}^{p_2,p_3} \,Y\). Let \(f \in \mathcal{F}_0^{-\mu /2, \mu /2}.\) Note that this class of mapping is a generator of \(\preceq _{con}^{-\mu /2, \mu /2}\) as Lemma 1 reads. Let \(T:\mathbb {R}\rightarrow \mathbb {R}\) with \(T(x)=x-(p_2+p_3)/2.\) Observe that \(P_X \circ T^{-1}(B)=P_{X-(p_2+p_3)/2}(B)\) for any \(B \in \mathcal{B}.\) By a change of variable (see, for instance, Halmos (1950)), we have that
It is not hard to prove that the map \(x \rightarrow f(x-(p_2+p_3)/2)\) belongs to the class \(\, \mathcal{F}_0^{p_2,p_3} \,\). In fact, if \(f=f_{p_1,-\mu /2,\mu /2,p_4,0}\) for some \(p_1 < -\mu /2\) and \(p_4> \mu /2\), then \(f(x-(p_2+p_2)/2)=f_{p_1+(p_2+p_3)/2,p_2,p_3,p_4+(p_2+p_3)/2 }(x).\) Since \(X \, \preceq _{con}^{p_2,p_3} \,Y\), we obtain that
and so \(X-(p_2+p_3)/2 \, \preceq _{con}^{-\mu /2, \mu /2} \, Y-(p_2+p_3)/2.\) The converse can be proved in a similar way. \(\square \)
Proof of Proposition 2
Assume that the condition \(X \, \preceq _{con}^{-\delta ,\delta } \,Y\) is satisfied.
Let \(t >0.\) Take the mapping \(f_{-\delta , -\delta ,\delta , \delta +t,0}\), that is, \(f_{-\delta , -\delta ,\delta , \delta +t,0}(x)=(x-\delta )I_{(\delta ,\delta +t]}(x)+tI_{(\delta +t,+\infty )}(x)\) for any \(x \in \mathbb {R}\).
By Lemma 2, \(E(f_{-\delta , -\delta ,\delta , \delta +t,0}(X))\le E(f_{-\delta , -\delta ,\delta , \delta +t,0}(Y))\) holds. Note that
which implies (i).
Let \(t<0.\) Take the mapping \(f_{-\delta +t,-\delta ,\delta ,\delta ,0}\). That mapping is given by \(f_{-\delta +t,-\delta ,\delta ,\delta ,0}(x)=\vert t \vert I_{(-\infty ,-\delta +t]}(x)+(-\delta -x)I_{(-\delta +t,-\delta ]}(x)\) for any \(x \in \mathbb {R}\).
By Lemma 2, \(E(f_{-\delta +t,-\delta ,\delta ,\delta ,0}(X)) \le E(f_{-\delta +t,-\delta ,\delta ,\delta ,0}(Y)).\) Now
what leads to (ii).
Now suppose that (i) and (ii) hold. Let \(f_{p_1,-\delta ,\delta ,p_4,0} \in \, \mathcal{F}_0^{-\delta ,\delta } \,\) \((p_1 < -\delta ,\, p_4> \delta )\). Note that \(f_{p_1,-\delta ,\delta ,p_4,0}= f_{(p_1+\delta )-\delta ,-\delta ,\delta ,\delta ,0} +f_{-\delta ,-\delta ,\delta ,\delta +(p_4-\delta ),0}.\) Conditions (i) and (ii), jointly with formulas (2) and (3), imply that \(E(f_{p_1,-\delta ,\delta ,p_4,0}(X)) \le E(f_{p_1,-\delta ,\delta ,p_4,0}(Y)),\) and so \(X \, \preceq _{con}^{-\delta ,\delta } \,Y\). \(\square \)
Proof of Proposition 3
Let \(t>0.\) We have that
Thus, formula (i) of Proposition 2 is equivalently to
for any \(t>0\).
On the other hand, if \(t<0\) then
As a consequence, condition (ii) in Proposition 2 is the same as
for any \(t<0.\) \(\square \)
Proof of Proposition 4
Observe that for any random variable W, \(F_{W_+}(x)=F_W(x)I_{[0,\infty )}(x)\) and \(F_{W_-}(x)=(1-F_W(-x^-))I_{[0,\infty )}(x)\).
When \(t>0\), we have that
and then, condition (i) of Proposition 3 is the same as
for any \(t \in \mathbb {R}\). By means of Theorem 4.A.2 in Shaked and Shanthikumar (2007), this is equivalent to \((X-\delta )_+ \preceq _{icv} (Y-\delta )_+\).
When \(t<0\), we have that
Therefore, condition (ii) of Proposition 3 can be rewritten as
The set of discontinuity points of an increasing map is at most countable; then, the above inequality is the same as
for any \(t<0\), or
for any \(t>0\). It is clear that this is the same as
for any \(t \in \mathbb {R}\). By Theorem 4.A.2 in Shaked and Shanthikumar (2007), this is \((X+\delta )_- \preceq _{icv} (Y+\delta )_-\). \(\square \)
Proof of Proposition 5
Assume that \(X \, \preceq _{con}^{p_2,p_3} \,Y\). Let \(f \in \mathcal{F}^{-p_3,-p_2}\). Consider \(T:\mathbb {R}\rightarrow \mathbb {R}\) with \(T(x)=-x\) for any \(x \in \mathbb {R}\). Note that \(P_X \circ T^{-1}=P_{-X}.\) By a change of variable
It is not hard to prove that if \(f \in \mathcal{F}^{-p_3,-p_2}\), then the mapping \(x \rightarrow f(-x)\) belongs to \(\, \mathcal{F}^{p_2,p_3} \,,\) and so
which proves that \(-X \, \preceq _{con}^{-p_3,-p_2} \, -Y\). The converse is implied by the proved part. \(\square \)
Proof of Proposition 6
Let \(T:\mathbb {R}\rightarrow \mathbb {R}\) with \(T(x)=\vert x\vert .\) Let \(f \in \, \mathcal{F}_0^{-\delta ,\delta } \,\). A change of variable, the symmetry of the distribution and \(f(0)=0\), imply that
Assume that \(X \, \preceq _{con}^{-\delta ,\delta } \,Y\). Let \(f \in \, \mathcal{F}_0^{-\delta ,\delta } \,\), thus \(f=f_{p_1,-\delta ,\delta ,p_4,0}\) for some \(p_1\) and \(p_4\) with \(p_1 < -\delta \) and \(p_4 > \delta \). Note that \(fI_{(0,\infty )}=f_{-\delta ,-\delta ,\delta ,p_4,0}\). Then
Therefore, we obtain that \(\vert X \vert \, \preceq _{con}^{-\delta ,\delta } \,\vert Y \vert .\)
Now let us suppose that \(\vert X \vert \, \preceq _{con}^{-\delta ,\delta } \,\vert Y \vert .\) Let \(f \in \, \mathcal{F}_0^{-\delta ,\delta } \,\). Note that the mapping \(x \mapsto f(-x)\) belongs to \(\, \mathcal{F}_0^{-\delta ,\delta } \,\). Thus
which concludes the result. \(\square \)
Proof of Corollary 3
It follows from Propositions 6 and 4. \(\square \)
Proof of Proposition 7
By Proposition 3, we have that
-
(i)
\(\int _{\delta }^{\delta +t} F_X(x)\, \hbox {d}x = \int _{\delta }^{\delta +t} F_Y(x)\, \hbox {d}x\) for any \(t>0\), and
-
(ii)
\(\int _{-\delta +t}^{-\delta } F_X(x)\, \hbox {d}x = \int _{-\delta +t}^{-\delta } F_Y(x)\, \hbox {d}x \) for any \(t<0\).
By the First Fundamental Theorem of Calculus, we obtain that \(F_X(\delta +t)=F_Y(\delta +t)\) for all \(t>0\) such that \(\delta +t\) is a continuity point of \(F_X\) and \(F_Y\). Using the right continuity of distributions functions and the density of the set of continuity points of both functions, we obtain that \(F_X(x)=F_Y(x)\) for any \(x \ge \delta .\) The same reasoning applied to condition (ii) provides that \(F_X(x)=F_Y(x)\) for any \(x \le -\delta .\) \(\square \)
Proof of Proposition 8
The condition \(S^-(f_Y-f_X)=2\) with sign sequence \(+,-,+\), implies that \(S^-(F_Y-F_X)=1\) with sign sequence \(+,-\) (see the proof of Theorem 3.A.44 in Shaked and Shanthikumar (2007)). The symmetry of the distributions implies that the crossing point is 0. Moreover, \(F_{\vert X \vert }(x)=(2F_X-2)I_{[0,\infty )}(x)\). Therefore, \(S^-(F_{\vert Y\vert }-F_{\vert X\vert })=0\) and \(F_{\vert Y\vert }\le F_{\vert X\vert }\), which is the same as \(\vert X\vert \preceq _{st}\vert Y\vert \). Since the mapping \(g_{\delta ,t}:\mathbb {R}\rightarrow \mathbb {R}\) with \(g_{\delta ,t}(x)=(x-\delta )_+\) is increasing, we conclude that \((\vert X\vert -\delta )_+ \preceq _{st}(\vert Y\vert -\delta )_+\). That implies \((\vert X\vert -\delta )_+ \preceq _{icv}(\vert Y\vert -\delta )_+\). Now Proposition 4 ensures that \(\vert X\vert \, \preceq _{con}^{-\delta ,\delta } \,\vert Y\vert \), and Proposition 6 proves the result. \(\square \)
Proof of Proposition 9
Let us see (i). We have \(F_{(X-\delta )_+}(x)=F_{X-\delta }(x)I_{[0,\infty )}(x)=F_X(x+\delta )I_{[0,+\infty )}(x)\) for any \(x \in \mathbb {R}\), and the same formula holds for the random variable Y. Thus if \(S^-(F_Y-F_X) \le 1\), we obtain that \(S^-(F_{(Y-\delta )_+}-F_{(X-\delta )_+}) \le 1\), and if the second number of sign changes is 1, so is the first number of sign changes, the sequence of signs being equal. Applying Theorem 4.A.22 (b) in Shaked and Shanthikumar (2007), we conclude that \((X-\delta )_+ \preceq _{icv} (Y-\delta )_+\).
On the other hand \(F_{(X+\delta )_-}(x)=(1-F_{(X+\delta )}(-x^-))I_{[0,\infty )}(x)=(1-F_X((-\delta -x)^-))I_{[0,\infty )}(x).\) As a consequence, we obtain that \(S^-(F_{(Y+\delta )_-}-F_{(X+\delta )_-}) \le S^-(F_Y-F_X)\), and if \(S^-(F_{(Y+\delta )_-}-F_{(X+\delta )_-})=1\) so is \(S^-(F_Y-F_X)=1\), sharing the same sequence of signs. By Theorem 4.A.22 (b) in Shaked and Shanthikumar (2007), we obtain that \((X+\delta )_-\preceq _{icv} (Y+\delta )_-\). Now Proposition 4 implies that \(X \, \preceq _{con}^{-\delta ,\delta } \,Y.\)
In relation to (ii), observe that \(F_{X_{(n)}}=F_X^n\). Therefore, \(S^-(F_{Y_{(n)}}-F_{X_{(n)}})=S^-(F_Y-F_X)\). Moreover, \(F_{Y_{(n)}}-F_{X_{(n)}}\) and \(F_Y-F_X\) share the same sign changes. Hence (ii) is obtained by (i).
Taking into account \(F_{X_{(1)}}=1-(1-F_X)^n\), statement (iii) can be obtained in a similar way. \(\square \)
Proof of Proposition 10
It holds that \(P_X \circ h_i^{-1}\) is equal to \(P_{h_i(X)}\) with \(i=1,2.\) Let \(f \in \, \mathcal{F}_0^{-\delta ,\delta } \,\). We have that
If \(x\in [0,+\infty )\), we have that \(h_1(x) \le h_2(x)\) and f is increasing on that set. On the other hand, if \(x \in (-\infty ,0)\), then \(h_1(x) \ge h_2(x)\) and on that subset the mapping f is decreasing. As a consequence
which proves the result. \(\square \)
Proof of Proposition 11
The case \(\alpha =0\) is trivial. Let \(\alpha >0.\) Consider \(T:\mathbb {R}\rightarrow \mathbb {R}\) with \(T(x)= \alpha x\). It holds that \(P_X \circ T^{-1}=P_{\alpha X}.\) Let \(f \in \mathcal{F}_0^{\alpha p_2, \alpha p_3}.\) By a change of variable,
If \(f \in \mathcal{F}_0^{\alpha p_2, \alpha p_3},\) then \(f=f_{p_1,\alpha p_2, \alpha p_3,p_4,0}\) for some \(p_1 < \alpha p_2\) and \(p_4 > \alpha p_3.\) It is not hard to prove that the mapping \(x \rightarrow f(\alpha x)\) is the function \(\alpha f_{p_1/\alpha , p_2, p_3,p_4/\alpha ,0}\), which belongs to the class \(\mathcal{F}_0^{p_2,p_3}\). As a consequence
Therefore, \(\alpha X \, \preceq _{con}^{\alpha p_2, \alpha p_3} \,\alpha Y\).
Now let \(\alpha <0\). By the proven part we conclude that \(-\alpha X \, \preceq _{con}^{-\alpha p_2, -\alpha p_3} \,-\alpha Y.\) Applying Proposition 5, we deduce that \(\alpha X \, \preceq _{con}^{\alpha p_3, \alpha p_2} \,\alpha Y\). \(\square \)
Proof of Proposition 12
Note that the mappings of \(\, \mathcal{F}_0^{p_2,p_3} \,\) are continuous and bounded. \(\square \)
Proof of Proposition 13
The stochastic order is integral which implies the result (see Theorem 2.4.2 in Müller and Stoyan (2002)). \(\square \)
Proof of Proposition 14
Clearly \(X-\delta \preceq _{st} X-\delta +a\). Then, \(X-\delta \preceq _{icv} X-\delta +a\). Observe that \((X-\delta )_+=X-\delta \,\, a.s.\) and \((X+a-\delta )_+=X+a-\delta \,\, a.s.\) Moreover, \((X+\delta )_-=0=(X+a+\delta )_- \,\,a.s.\) Proposition 4 proves the result. \(\square \)
Proof of Proposition 15
In accordance with Proposition 5, \(X \, \preceq _{con}^{-\delta ,\delta } \,X+b\) is equivalent to \(-X \, \preceq _{con}^{-\delta ,\delta } \,-X-b.\) Now the result is a consequence of Proposition 14. \(\square \)
Proof of Proposition 16
A generator of the bidirectional order is the set \(\mathcal{F}=\{\,f:\mathbb {R}\rightarrow \mathbb {R}\mid f \hbox { is bounded, increasing in } (0,\infty ), \hbox { decreasing in }(-\infty ,0)\) and with minimum at the point \(0 \,\}\) (Proposition 5 in López-Díaz (2010)). Observe that \(\mathcal{F}_0^{-\delta ,\delta } \subset \mathcal{F},\) which leads to the result. \(\square \)
Proof of Proposition 17
By Proposition 16, \(X \preceq _{bd} Y\) implies \(X \, \preceq _{con}^{-\delta ,\delta } \,Y\) for any \(\delta >0\).
Now suppose that \(X \, \preceq _{con}^{-\delta ,\delta } \,Y\) for any \(\delta >0\). The condition \(X \preceq _{bd} Y\) is the same as \(F_X-F_Y\) pivots at 0, that is, \(F_X(t)-F_Y(t) \ge 0\) for any \(t \ge 0\) and \(F_X(t)-F_Y(t) \le 0\) for any \(t < 0\). Assume that \(X \preceq _{bd} Y\) is false. Therefore, there exists \(t_0 \ge 0\) with \(F_X(t_0) < F_Y(t_0)\), or there is \(t_0 <0\) satisfying that \(F_X(t_0) > F_Y(t_0)\). Consider now the first possibility. By the right continuity of distribution functions, we can assume that \(t_0 >0.\) For the same reason, there exists \(\varepsilon >0\) such that \(F_X < F_Y\) on \((t_0,t_0+\varepsilon ),\) which is a contradiction with Proposition 3 (i). The case of the existence of \(t_0<0\) with \(F_X(t_0) > F_Y(t_0)\), can be analyzed in the same way, using (ii) in Proposition 3. Thus, we conclude that \(X \preceq _{bd} Y\). \(\square \)
Proof of Proposition 18
We have that \(X \preceq _{peak} Y\) implies that \(X-EX \preceq _{bd} Y-EY\) (Corollary 9 in López-Díaz (2010)). The result follows from Proposition 16. \(\square \)
Proof of Proposition 19
The relation \(X \preceq _{w} Y\) is equivalent to \(X-X' \preceq _{bd} Y-Y'\) (Corollary 10 in López-Díaz (2010)), and so we have the result. \(\square \)
Proof of Proposition 20
The sequences of mappings \(\{(x-1/m)_+\}_m\) and \(\{(x+1/m)_-\}_m\) are increasing. By the monotone convergence theorem, \(\lim _m E((X-1/m)_+)= E(\lim _m (X-1/m)_+)=EX_+\) and \(\lim _m E((X+1/m)_-)= E(\lim _m (X+1/m)_-)=EX_-\). On the other hand, \(\lim _m (X-1/m)_+=X_+\) and \(\lim _m (X+1/m)_-=X_-\) in the weak convergence since we have the pointwise convergence. The same results are satisfied by random variable Y.
By Proposition 4 in this manuscript, Theorem 1.5.9 in Müller and Stoyan (2002) and the relation between \(\preceq _{icx}\) and \(\preceq _{icv}\), we conclude that \(X_+ \preceq _{icv} Y_+\) and \(X_- \preceq _{icv} Y_-\).
If X and Y are negative a.s., then \(Y_+ =0=X_+ \,\,a.s.\), \(X_-=-X\) and \(Y_-=-Y\,\,a.s.\), and so we conclude that \(Y \preceq _{icx} X\). When X and Y are positive a.s., \(Y_- =0=X_-\,\,a.s.\), \(X_+=X\) and \(Y_+=Y\,\,a.s.\), which implies that \(X \preceq _{icv} Y.\) \(\square \)
Proof of Corollary 5
It is a consequence of Proposition 20 and Theorem 1.5.3 in Müller and Stoyan (2002). \(\square \)
Proof of Example 5
Proposition 19 in López-Díaz (2010) reads that \(\sigma _X \le \sigma _Y\) implies that \(X-\mu _X \preceq _{bd} Y-\mu _Y\), and as a consequence of Proposition 16, we deduce that \(X-\mu _X \, \preceq _{con}^{-\delta ,\delta } \,Y-\mu _Y\).
Let us see the converse. We have that \(X-\mu _X \, \preceq _{con}^{-\delta ,\delta } \,Y-\mu _Y\). Suppose that \(\sigma _Y <\sigma _X\). By the proven part, we obtain that \(Y-\mu _Y \, \preceq _{con}^{-\delta ,\delta } \,X-\mu _X.\) Applying Proposition 7, we deduce that \(F_{X-\mu _X}(t)=F_{Y-\mu _Y}(t)\) for any \(t \in (-\infty ,-\delta ] \cup [\delta ,+\infty )\). By Proposition 3 and the First Fundamental Theorem of Calculus, we deduce that the density mappings of \(X-\mu _X\) and \(Y-\mu _Y\) are the same on \((-\infty ,-\delta ] \cup [\delta ,+\infty )\), and so \(\sigma _X=\sigma _Y,\) which contradicts the assumption \(\sigma _Y <\sigma _X.\) Therefore, \(\sigma _X \le \sigma _Y\). \(\square \)
Proof of Example 6
Lemma 1 in Finner et al. (2007) reads that the density mappings of X and Y satisfy that \(S^-(f_Y-f_X)=2\) and the sign sequence is \(+,-,+\). Now the result follows from Proposition 8. \(\square \)
Proof of Example 7
Lemma 1 and Theorem 3 in Finner et al. (2007) imply that \(S^-(f_Y-f_X)=2\) and the sign sequence is \(+,-,+\). Proposition 8 proves the result. \(\square \)
Proof of Proposition 21
The result follows from Example 5, note that \(X_t \sim _{st} N(r_Xt,\sigma _X \sqrt{t})\) and \(Y_t \sim _{st} N(r_Yt,\sigma _Y \sqrt{t})\). \(\square \)
Proof of Proposition 22
Proposition 21 reads that \(\sigma _Y \ge \sigma _X\) if and only if \(X_t-r_Xt \, \preceq _{con}^{-\delta ,\delta } \,Y_t-r_Yt\) for any \(t \in [0,T]\) and any \(\delta >0.\) Now take \(p_2=k-\delta \) and \(p_3=k+\delta \) with \(k \in \mathbb {R}\) and \(\delta >0\) in Proposition 1, which proves the result. \(\square \)
Proof of Proposition 23
We will prove the result by means of Proposition 3.
Let \(z \le -\delta \). We have that \(F_{X'_t}(z)=P(X'_t \le z)=P(X_t \le c e^{rt}+z)\). Assume that z satisfies that \(c e^{rt}+z>0\), that is, \(-c e^{rt}<z\), otherwise the above probability is equal to 0. Take \(m_z=\ln (1+z/ce^{rt}),\) thus \(c e^{rt}+z=ce^{rt+m_z}.\) The above probability satisfies that
The same result holds for the process \((Y'_t)_{t \in [0,T]}\).
Suppose that condition (ii) in Proposition 3 holds.
Recall that \(B_t \sim _{st} \widetilde{B}_t \sim _{st} N(0,\sqrt{t})\). By the continuity of \(F_{B_t}\) and \(F_{\widetilde{B}_t}\), we obtain that
Observe that \(m_{-\delta }=\ln (1+(-\delta )/ce^{rt})\) is negative, and so \(\sigma _Y \ge \sigma _X\). Conversely, if \(\sigma _Y \ge \sigma _X\), then
for any \(z \le -\delta \) since \(m_z\) is negative, and so condition (ii) in Proposition 3 is satisfied. Therefore, statement (ii) in Proposition 3 is equivalent to \(\sigma _Y \ge \sigma _X\). Now take \(z \ge \delta \). We have that \(F_{X'_t}(z)=P(X'_t \le z)=P(X_t \le c e^{rt}+z)=P(X_t \le c e^{rt+m_z})\), where \(m_z=\ln (1+z/ce^{rt}),\) note that in this case \(m_z>0.\) Thus,
Assume that condition (i) in Proposition 3 is satisfied. By the right continuity of distribution functions, we obtain that
Since \(\sigma _Y \ge \sigma _X\) by the first part of the proof, we conclude that \(m_\delta \ge {t \over 2} \sigma _X \sigma _Y\), that is, \(\delta \ge ce^{rt}(e^{{t \over 2} \sigma _X \sigma _Y} -1)\). Conversely, if \(\delta \ge ce^{rt}(e^{{t \over 2} \sigma _X \sigma _Y} -1)\), that is, \(m_\delta \ge {t \over 2} \sigma _X \sigma _Y\), then \(m_z \ge m_\delta \ge {t \over 2} \sigma _X \sigma _Y\) for any \(z \ge \delta \), and so \(F_{B_t} ( {1 \over 2} \sigma _X t+ {m_z \over \sigma _X}) \ge F_{\widetilde{B}_t} ( {1 \over 2} \sigma _Y t+ {m_z \over \sigma _Y})\), which concludes (i) in Proposition 3, and so the proof of the result. \(\square \)
Proof of Proposition 24
It follows applying Propositions 23 and 1. \(\square \)
Proof of Proposition 25
Statement (i) is clear.
In relation to (ii), the real mapping on \(\mathbb {R}\) given by \(x \rightarrow S^x_{p_1,p_2,k_1,k_2}\) is increasing for any \(p_1,p_2,k_1,k_2 \in \mathbb {R}\) with \(p_1 \le p_2\). Therefore, \(X \preceq _{st} Y\) implies that \(E S^X_{p_1,p_2,k_1,k_2} \le E S^Y_{p_1,p_2,k_1,k_2}\) for all \(p_1,p_2,k_1,k_2 \in \mathbb {R}\) with \(p_1 \le p_2\).
Conversely, note that \(E S^X_{p_1,p_2,k_1,k_2}=\pi _X(p_1)-\pi _X(p_2)+k_2-k_1\). Thus, \(E S^X_{p_1,p_2,k_1,k_2} \le E S^Y_{p_1,p_2,k_1,k_2}\) for all \(p_1,p_2,k_1,k_2 \in \mathbb {R}\) with \(p_1 \le p_2\), implies that \(\pi _X(p_1)-\pi _X(p_2) \le \pi _Y(p_1)-\pi _Y(p_2)\). That is \(\pi _Y - \pi _X\) is decreasing. By Theorem 1.5.13 in Müller and Stoyan (2002), we obtain that \(X \preceq _{st} Y.\)
Statment (iii) follows from Theorem 1.5.7 in Müller and Stoyan (2002).
For the last statement, note that the real mapping on \(\mathbb {R}\) defined by \(x \rightarrow ST^x_{p,k_1,k_2}\) is convex for any \(p,\,k_1,\, k_2 \in \mathbb {R}.\) Thus, \(X \preceq _{cx} Y\) leads to \(EST^X_{p,k_1,k_2} \le EST^Y_{p,k_1,k_2}\) for all \(p,k_1,k_2 \in \mathbb {R}\).
For the converse, take \(k_1=k_2=0.\) Now note that \( \lim _{p' \rightarrow - \infty } {1 \over 2}(ST^X_{p,0,0} + ST^X_{p',0,0}-(p-p'))=C^X_{p,0}.\) Since \(E(ST^X_{p,0,0}+ST^X_{p',0,0}) \le E(ST^Y_{p,0,0}+ST^Y_{p',0,0})\) for any \(p,p' \in \mathbb {R}\), the dominated convergence theorem implies that \(E(C^X_{p,0}) \le E(C^Y_{p,0})\). By Theorem 1.5.7 in Müller and Stoyan (2002), \(X \preceq _{icx} Y\) holds.
On the other hand, since \(ST^X_{p,0,0}=(X-p)_+ + (p-X)_+\) we obtain that \(\lim _{p \rightarrow -\infty } ST^X_{p,0,0}+p=X \hbox { and } \lim _{p \rightarrow +\infty } ST^X_{p,0,0}-p=-X.\) By the dominated convergence theorem, we have that \( \lim _{p \rightarrow - \infty } E(ST^X_{p,0,0}) + p=EX \hbox { and } \lim _{p \rightarrow + \infty } E(ST^X_{p,0,0}) - p=-EX.\) Therefore, we deduce that \(EX=EY,\) which in conjunction with \(X \preceq _{icx} Y\) implies that \(X \preceq _{cx} Y.\) \(\square \)
Rights and permissions
About this article
Cite this article
López-Díaz, M.C., López-Díaz, M. & Martínez-Fernández, S. Stochastic orders to approach investments in condor financial derivatives. TEST 27, 122–146 (2018). https://doi.org/10.1007/s11749-017-0537-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-017-0537-3
Keywords
- Call option
- Condor derivative
- (Geometric) Brownian movement
- Increasing concave order
- Put option
- Stochastic order