Skip to main content
SpringerLink
Log in

Detection of Cracks in Adhesively Bonded Double-Strap Joints Using Artificial Neural Network Method

  • Technical Article---Peer-Reviewed
  • Published:
Journal of Failure Analysis and Prevention Aims and scope Submit manuscript

Abstract

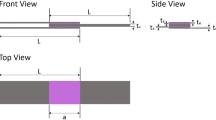
This study aims to survey the effects of crack length on the natural frequencies and mode shapes of adhesively bonded double-strap joints (DSJs) in the models with different adherend thicknesses and different adhesive ductility. Hence, the results of these analyses are used as a method of crack detection inside the adhesive layer. For this purpose, a rich database of results for DSJ models with cracks in length of 0 ≤ l C ≤ 10 mm were used for the aim of training the artificial neural network (ANN) algorithms. Subsequently, the results obtained from ANN models can be used to estimate the existence of crack and its length. The results show that the natural frequencies of the models with different adherend thicknesses and different adhesive ductility follow a logical trend, by which detection of cracks is possible for a wide range of geometries and material properties, using ANN analysis. By contrast, the results show that mode shapes are not affected by cracks. Therefore, the mode shapes are not useful characteristics for judgments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. R.D. Adams, N.A. Peppiatt, Stress analysis of adhesive-bonded lap joints. J. Strain Anal. 9(3), 185–196 (1974)

    Article  Google Scholar 

  2. R.D. Adams, W.C. Wake, Structural Adhesive Joints in Engineering (Elsevier Applied Science Publishers, Amsterdam, 1984)

    Book  Google Scholar 

  3. A.J. Kinloch, The science of adhesion. 1. Surface and interfacial aspects. J. Mater. Sci. 15, 2141–2166 (1980)

    Article  Google Scholar 

  4. L. Tong, Analysis and Design of Structural Bonded Joints/by Liyong Tong, Grant P. Steven (Kluwer Academic, Dordrecht, 1999)

    Book  Google Scholar 

  5. W.C. Wake, Adhesion and adhesives: science and technology A. J. Kinloch (Chapman and Hall, London, 1987). pp. xii + 441, price £35.00. ISBN 0-412-27440-X, Br. Polym. J., 20(3), 300–300 (1988)

  6. X. He, S.O. Oyadiji, Influence of adhesive characteristics on the transverse free vibration of single lap-jointed cantilevered beams. J. Mater. Process. Technol. 119(1–3), 366–373 (2001)

    Article  Google Scholar 

  7. K.H. Almitani, R. Othman, Analytical solution of the harmonic response of visco-elastic adhesively bonded single-lap and double-lap joints. Int. J. Adhes. Adhes. 71, 55–65 (2016)

    Article  Google Scholar 

  8. S.B. Ingole, A. Chatterjee, Vibration analysis of single lap adhesive joint: experimental and analytical investigation. J. Vib. Control 17(10), 1547–1556 (2011)

    Article  Google Scholar 

  9. X. He, Finite element analysis of torsional free vibration of adhesively bonded single-lap joints. Int. J. Adhes. Adhes. 48, 59–66 (2014)

    Article  Google Scholar 

  10. A. Kaya, M.S. Tekelioğlu, F. Findik, Effects of various parameters on dynamic characteristics in adhesively bonded joints. Mater. Lett. 58(27–28), 3451–3456 (2004)

    Article  Google Scholar 

  11. R. Gunes, M. Kemal Apalak, M. Yildirim, I. Ozkes, Free vibration analysis of adhesively bonded single lap joints with wide and narrow functionally graded plates. Compos. Struct. 92(1), 1–17 (2010)

    Article  Google Scholar 

  12. Y. Du, L. Shi, Effect of vibration fatigue on modal properties of single lap adhesive joints. Int. J. Adhes. Adhes. 53, 72–79 (2014)

    Article  Google Scholar 

  13. U. Andreaus, P. Baragatti, Fatigue crack growth, free vibrations, and breathing crack detection of aluminium alloy and steel beams. J. Strain Anal. Eng. Des. 44(7), 595–608 (2009)

    Article  Google Scholar 

  14. U. Yuceoglu, O. Güvendik, Effects of position (or location) of non-centrally bonded symmetric double lap joint (or symmetric double doubler joint) on bending vibrations of composite mindlin plates or panels. in ASME 2010 International Mechanical Engineering Congress and Exposition (American Society of Mechanical Engineers, 2010) pp. 595–618

  15. S. Haykin, Neural Networks: A Comprehensive Foundation (Prentice Hall PTR, Upper Saddle River, 1998)

    Google Scholar 

  16. M.K. Apalak, R. Ekici, M. Yildirim, Optimal design of an adhesively bonded corner joint with single support based on the free vibration analysis. J. Adhes. Sci. Technol. 20(13), 1507–1528 (2006)

    Article  Google Scholar 

  17. M. Kemal Apalak, R. Ekici, M. Yildirim, Free vibration analysis and design of an adhesively bonded corner joint with double support. J. Adhes. 83(11), 957–986 (2007)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran

    Bahman Paygozar

  2. Department of Mechanical Engineering, Azarbaijan Shahid Madani University, Tabriz, Iran

    Mohammad Ali Saeimi Sadigh

Authors
  1. Bahman Paygozar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad Ali Saeimi Sadigh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bahman Paygozar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Paygozar, B., Sadigh, M.A.S. Detection of Cracks in Adhesively Bonded Double-Strap Joints Using Artificial Neural Network Method. J Fail. Anal. and Preven. 17, 1023–1030 (2017). https://doi.org/10.1007/s11668-017-0338-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11668-017-0338-8

Keywords

Search

Navigation