Skip to main content
SpringerLink
Log in

Finite Element Analysis of Micromechanical Progressive Failure Properties of Glass Fiber/Phenolic Resin Composites by Monte Carlo Simulation

  • Technical Article---Peer-Reviewed
  • Published:
Journal of Failure Analysis and Prevention Aims and scope Submit manuscript

Abstract

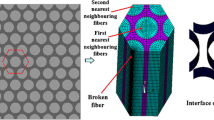
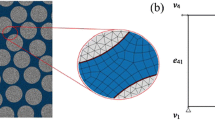
This paper studies the micromechanical progressive failure properties of glass fiber/phenolic resin composites by finite element analysis and experiments. First, a set of theoretical methods on the failure criteria and damage evolution of fiber, matrix, and interface are introduced, which include Monte Carlo simulation on random fiber fracture, damage evolution and stiffness degradation of matrix based on thermodynamic theory, an exponential cohesive model for interface debonding, and a strain localization-based Mori–Tanaka homogenization method. Second, the proposed model is implemented using ANSYS PARAMETRIC DESIGN LANGUAGE (ANSYS-APDL) that uses the restart numerical technique. In order to predict the tensile strength of the composites, the numerical convergence issue is solved by introducing viscous effect into the stiffness equations. Finally, numerical results in terms of the damage evolution behaviors and tensile strengths of composite microstructures are validated by tensile experiments and acoustic emission tests on unidirectional glass fiber/phenolic composites.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. F. Dharmawan, G. Simpson, I. Herszberg, S. John, Mixed mode fracture toughness of GFRP composites. Compos. Struct. 75, 328–338 (2006)

    Article  Google Scholar 

  2. P.F. Liu, J.K. Chu, S.J. Hou, J.Y. Zheng, Micromechanical damage modeling and multiscale progressive failure analysis of composite pressure vessel. Comput. Mater. Sci. 60, 137–148 (2012)

    Article  Google Scholar 

  3. P.F. Liu, J.Y. Zheng, Progressive failure analysis of carbon fiber/epoxy composite laminates using continuum damage mechanics. Mater. Sci. Eng. A. 485(1–2), 711–717 (2008)

    Article  Google Scholar 

  4. P.F. Liu, Z.P. Gu, Y.H. Yang, X.Q. Peng, A nonlocal finite element model for progressive failure analysis of composite laminates. Compos. Part B Eng. 86, 178–196 (2016)

    Article  Google Scholar 

  5. P.F. Liu, J.K. Chu, Y.L. Liu, J.Y. Zheng, A study on the failure mechanisms of carbon fiber/epoxy composite laminates using acoustic emission. Mater. Des. 37, 228–235 (2012)

    Article  Google Scholar 

  6. P.F. Liu, J. Yang, B. Wang, Z.F. Zhou, J.Y. Zheng, A study on the intralaminar damage and interlaminar delamination of carbon fiber composite laminates under three-point bending using acoustic emission. J. Fail. Anal. Prev. 15(1), 101–121 (2015)

    Article  Google Scholar 

  7. X.K. Li, P.F. Liu, Delamination analysis of carbon fiber composites under dynamic loads using acoustic emission. J. Fail. Anal. Prev. 16, 142–153 (2016)

    Article  Google Scholar 

  8. L.P. Canal, J. Segurado, J. LLorca, Failure surface of epoxy-modified fiber-reinforced composites under transverse tension and out-of-plane shear. Int. J. Solids Struct. 46(11-12), 2265–2274 (2009)

    Article  Google Scholar 

  9. E. Totry, C. González, J. LLorca, Influence of the loading path on the strength of fiber-reinforced composites subjected to transverse compression and shear. Int. J. Solids Struct. 45(6), 1663–1675 (2008)

    Article  Google Scholar 

  10. T.J. Vaughan, C.T. McCarthy, Micromechanical modelling of the transverse damage behaviour in fibre reinforced composites. Compos. Sci. Technol. 71(3), 388–396 (2011)

    Article  Google Scholar 

  11. J. Andersonsa, R. Joffeb, M. Hojoc, S. Ochiaic, Glass fibre strength distribution determined by common experimental methods. Compos. Sci. Technol. 62, 131–145 (2002)

    Article  Google Scholar 

  12. S.K. Ha, K.K. Jin, Y. Huang, Micro-mechanics of failure MMF for continuous fiber reinforced composites. J. Compos. Mater. 42, 1873–1895 (2008)

    Article  Google Scholar 

  13. X.P. Xu, A. Needleman, Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 42(9), 1397–1434 (1994)

    Article  Google Scholar 

  14. J.D. Eshelby, The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. A 241, 376–396 (1957)

    Article  Google Scholar 

  15. R. Hill, A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13, 213–222 (1965)

    Article  Google Scholar 

  16. T. Mori, K. Tanaka, Average stress in the matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574 (1973)

    Article  Google Scholar 

Download references

Acknowledgments

Dr. P.F. Liu would sincerely like to thank the support by the National Key Fundamental Research and Development Project of China (No. 2015CB057603), the National Natural Science Funding of China (No. 51375435), and Aerospace Science and Technology Innovation Funding (No. GFJG-112108-E81504).

Author information

Authors and Affiliations

  1. Institute of Chemical Machinery and Process Equipment, Zhejiang University, Hangzhou, 310027, China

    P. F. Liu & X. K. Li

  2. Institute of Aerospace Materials and Technology Research, Chinese Academy of Launch Vehicle Technology, Beijing, 100076, China

    J. C. Pang

Authors
  1. P. F. Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. K. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. C. Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. F. Liu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, P.F., Li, X.K. & Pang, J.C. Finite Element Analysis of Micromechanical Progressive Failure Properties of Glass Fiber/Phenolic Resin Composites by Monte Carlo Simulation. J Fail. Anal. and Preven. 16, 1108–1120 (2016). https://doi.org/10.1007/s11668-016-0192-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11668-016-0192-0

Keywords

Search

Navigation