Skip to main content
SpringerLink
Log in

Analysis of Loess Slope Stability Considering Cracking and Shear Failures

  • Technical Article---Peer-Reviewed
  • Published:
Journal of Failure Analysis and Prevention Aims and scope Submit manuscript

Abstract

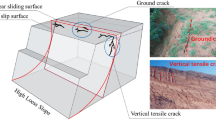
The cracks caused by tension are commonly observed on the upper border of loess slope. Most researchers assume that shear failure is the main reason for slope instability. The existing cracks and their development are not fully considered. The finite element method is applied widely in the numerical simulations of slope stability, but it converges and time problems must be considered when a crack occurs. The extended finite element method provides a new way to solve discontinuous media problems. In this paper, a composite model of cracking and shear failure is introduced. The extended finite element method was used to simulate the cracking in loess slope. The model used here had a unified enrichment function and the enriched freedom had a clear physical meaning. Numerical analyses were performed and the simulation results showed that the stress field redistributes. The crack propagated almost vertically at the beginning. The slope stability safety factor was less than that obtained without considering tension failure. Furthermore, the critical sliding surface was determined. This model can be used for analyzing the stability of loess slope and provides a reference for slope safety analyses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

N(x):

Shape function

u(x):

Displacement function

I,J :

No. of nodes

\(\varPsi\) :

Level set function of the crack surface

\(\phi\) :

Level set function of the crack tip

\(\hat{t}\) :

Tangent vector of the crack tip

σ3 :

Principal stress

\(z_{0}\) :

Crack depth of retaining wall

\(\gamma\) :

Bulk density

\(K_{\text{p}}\) :

Coefficient of passive pressure

References

  1. D.J. Li et al., Stability analysis of loess slope with hidden hole by numerical methods. Appl. Mech. Mater. 170–173, 306–311 (2012)

    Article  Google Scholar 

  2. D.V. Griffiths, P.A. Lane, Slope stability analysis by finite elements. Geotechnique 49(3), 387–403 (1999)

    Article  Google Scholar 

  3. J.M. Duncan, State of the art: limit equilibrium and finite element analysis of slopes. J. Geotech. Eng. 122(7), 577–595 (1996)

    Article  Google Scholar 

  4. D.Y. Zhu, A method for locating critical slip surfaces in slope stability analysis. Can. Geotech. J. 38(2), 328–337 (2001)

    Article  Google Scholar 

  5. M. Vafaeian, R. Abbaszadeh, Laboratory model tests to study the behavior of soil wall reinforced by weak reinforcing layers. Int. J. Eng. Trans. B Appl. 21(4), 361–373 (2008)

    Google Scholar 

  6. Z. Ding-Bang et al., Physical model test and numerical simulation study of deformation mechanism of wall rock on open pit to underground mining. Int. J. Eng. Trans. B Appl. 27(11), 1795–1802 (2014)

    Google Scholar 

  7. R. Qhaderi, M. Vafaeian, A parametric study of the behavior of geosynthetic reinforced soil slopes. Int. J. Eng. Trans. B Appl. 18(4), 371–389 (2005)

    Google Scholar 

  8. D. Nezamolmolki, A. Aftabi, Free vibration analysis of a sloping-frame: closed-form solution versus finite element solution and modification of the characteristic matrices. Int. J. Eng. Trans. A 28(3), 378–386 (2015)

    Google Scholar 

  9. Z.G. Wang et al., Discussion on the formation mechanism of vertical joints in loess. Sci. China Ser. B 23(7), 765–770 (1993)

    Google Scholar 

  10. Z. Dai, Z. Lium et al., Numerical analysis of soil slope stability considering tension and shear failures. Chin. J. Rock Mech. Eng. 27(2), 375–382 (2008)

    Google Scholar 

  11. X. Jin, L. Chen, Y. Zhang, Application of FEM strength reduction method to geotechnical engineering with the consideration of tension and shear failures. J. Chongqing University. 36(8), 97–104 (2013)

    Google Scholar 

  12. T. Belyschko, T. Black, Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 45, 601–620 (1999)

    Article  Google Scholar 

  13. P. Areias, T. Belytschko, Analysis of three-dimensional crack initiation and propagation using the extended finite element method. Int. J. Numer. Methods Eng. 63(5), 760–788 (2005)

    Article  Google Scholar 

  14. P.F. Liu, B.J. Zhang, J.Y. Zheng, Finite element analysis of plastic collapse and crack behavior of steel pressure vessels and piping using XFEM. J. Fail. Anal. Prev. 12(6), 707–718 (2012)

    Article  Google Scholar 

  15. M. Toolabi et al., Dynamic analysis of a viscoelastic orthotropic cracked body using the extended finite element method. Eng. Fract. Mech. 109, 17–32 (2013)

    Article  Google Scholar 

  16. J.H. Song, P.M.A. Areias, T. Belytschko, A method for dynamic crack and shear band propagation with phantom nodes. Int. J. Numer. Methods Eng. 67, 868–893 (2006)

    Article  Google Scholar 

  17. Stolarska et al., Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Methods Eng. 51(8), 943–960 (2001)

    Article  Google Scholar 

  18. Y.U. Jialin et al., Integration scheme for discontinuities in the extended finite element method. J. Tsinghua University. 49(3), 351–354 (2009)

    Google Scholar 

  19. J.M. Chang, H.P. Feng, Crack growth simulation in concrete beam based on extended isoparametric finite element method under quadrature without sub-area. J. Shijiazhuang Tiedao University. 26(3), 91–93 (2013)

    Google Scholar 

  20. Y.S. Zhang, H.C. Wang, Numerical simulation of the stability of high sand loess slopes. J. Geomech. 10(4), 357–365 (2004)

    Google Scholar 

Download references

Acknowledgments

This project is financially supported by the Natural Science Foundation of China (51478279) and the Scientific Research Foundation of Hebei Education Department (QN2015117). We gratefully acknowledge the assistance of the members in the Unsaturated Lab in Shijiazhuang Tiedao University.

Author information

Authors and Affiliations

  1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang, 050043, Hebei, People’s Republic of China

    Jianmei Chang, Siwen Song & Huaiping Feng

Authors
  1. Jianmei Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Siwen Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huaiping Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huaiping Feng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chang, J., Song, S. & Feng, H. Analysis of Loess Slope Stability Considering Cracking and Shear Failures. J Fail. Anal. and Preven. 16, 982–989 (2016). https://doi.org/10.1007/s11668-016-0174-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11668-016-0174-2

Keywords

Search

Navigation