Brief Background History

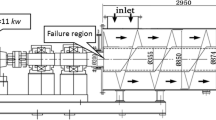
A single part of the broken shaft (50.8 mm; i.e., 2-inches nominal diameter), along with one being still in operation, is shown in Fig. 1. The matched piece (2nd half) of the fractured shaft was not available (probably sank after fracture). Both shafts were driven by a dual heavy duty ship engine (2 × 720 HP), transmitting rotational motion to the propellers, and they have been in service for almost 14 years. Shaft fracture, during navigation, led to significant loss of engine power and temporary loss of vessel stability, without any additional safety-related consequence. A simplified drawing that shows a general layout of the shaft and the related components along with the fracture location is shown in Fig. 2. The above incident led to the activation of a failure analysis procedure in order to evaluate the cause of failure and recommend preventive measures to minimize the risk of recurrence.

Fig. 1
figure 1

Macrograph showing the fractured propeller shaft and the unbroken twin member shaft (as received condition)

Full size image
Fig. 2
figure 2

Simplified drawing of the propeller shaft and the fracture location

Full size image

Analytical Techniques

Macrofractographic evaluation was performed using a stereomicroscope. Chemical analysis for steel grade identification was conducted using optical emission spectrometry. Hardness testing was performed using a universal hardness tester employing standard Rockwell C technique according to ASTM E-18 and Vickers hardness technique under 5 kg-force applied load according BS EN ISO 6507-1 standard. In addition, high-magnification fractographic observations were conducted on ultrasonically cleaned specimens, using a scanning electron microscope with a secondary electron detector for topographic evaluation and an energy dispersive x-ray spectrometer for elemental analysis.

Investigation Results

The chemical composition of the shaft sample, analyzed by optical emission spectrometry, is presented in Table 1. The material composition matches to the special high-alloy stainless steel grade, which is almost equivalent to AISI XM-19/UNS S20910 standard steel grade (austenitic steel), see Ref. [1]. This high-alloy stainless steel offers exceptional corrosion resistance in combination to high strength and toughness.

Table 1 Chemical composition of the shaft steel and approximate equivalent steel grade (wt.%)
Full size table

Hardness distribution (cross-sectional) obtained by employing Rockwell C and Vickers testing techniques is shown in Table 2. Vickers and HRC measurements are also in close agreement to the values obtained from standard hardness conversion tables. Ultimate tensile strength level, estimated from hardness, varied within ca. 1000–1200 MPa (~145 to 174 ksi).

Table 2 Hardness test results and estimated tensile strength
Full size table

Signs of distortion due to potential shaft misalignment were not identified during rotation. Macrofractographic investigation showed clear evidence of the occurrence of fatigue failure mechanism (Figs. 3 and 4). No visible shaft distortion and essentially flat fracture surface indicated the operation fatigue caused under complex rotational/in-plane/reversed bending loading mode [2, 3]. Industrial machine elements and engine components, subjected to various complex stress states, such as transmission of rotational motion or behaving as cantilever beams sustaining high bending moments, suffered from torsional overload and fatigue failures [4–9].

Fig. 3
figure 3

(a) Macrograph of the fracture surface and (b) macrofractographic image showing a close-up view of the fracture surface (“collage” made by superposition of specific areas) outlining the distinct fracture zones

Full size image
Fig. 4
figure 4

(a) Optical stereomicrograph of the fatigue crack propagation zone (FCP), showing the presence of beach marks indicating the initiation site; (b) detail of (a)

Full size image

Fatigue crack in the present case is clearly initiated from shaft circumference and propagated to the interior forming a characteristic macroscopic smooth surface pattern. Surface topography displays evidence of clearly defined beach marks, which evolved as concentric rings (Fig. 4). Beach marks or crack arrest marks constitute crack front progression marks that formed due to intermittent loading and/or development of compressive stress state ahead of the crack tip. Surface flaws, such as pits, grooves, dents etc., serve as crack initiation sites since they cause increase of local stress concentration factor (K t). Ratchet marks are also another fatigue characteristic feature (see right part of Fig. 3a), indicating the presence of multiple crack initiation sites and high stress concentration, see also Ref. [5]. Furthermore, triangular shape ratchet areas may also indicate the occurrence of complex stress state including torsional loading mode.

Secondary electron imaging (SEI) micrographs showed at a higher magnification the morphology of the various fracture zones on the shaft fracture surface (Fig. 5). The fatigue zone revealed mainly smeared areas from friction between crack mating surfaces with extensive secondary cracking (Fig. 5a, b). Moreover, poorly resolved striations were shown in isolated areas as depicted in Fig. 5c. Fatigue striations, a surface feature of fatigue crack propagation zone, constitute a microscopic fingerprint of the operation of cyclic loading. Striation pattern is formed by blunting and re-sharpening of the crack tip during stress cycling. Mean striation spacing corresponds to the average advancement of fatigue crack per load cycle. General aspects of fatigue fractographic features and the corresponding formation mechanism are also reported in Ref. [10].

Fig. 5
figure 5

SEM micrographs showing details of fracture surface topography: (a) fatigue crack propagation zone (FCP), (b) detail of (a), (c) poorly resolved fatigue striations; the arrows show the direction of crack propagation. The actual striation spacing corresponds to the local crack advancement rate per load cycle (da/dN); (d) the rough overload area showing quasi-cleavage features

Full size image

Fast or instantaneous fracture occurred when the residual cross-sectional area reached a critical size, becoming unable to support the operating load. Final fracture surface, accomplished via overload, showed a rough morphology, having a triangular and a off-center circular shape (slightly projected out), while its extent indicates low operating stress level (Fig. 3). The dominant type of the ultimate failure mode is dictated by the material properties and on the other hand by the existing service conditions (e.g., temperature, strain rate, local constraints). Areas that resemble to “quasi-cleavage steps,” formed as a result of brittle transgranular overload, were observed in the final fracture area (Fig. 5d).

Fatigue crack initiation area was viewed under low power stereomicroscope and under SEM (Fig. 6). The fatigue origin is located on a dent/pit coming most probably from mechanical damage during operation or handling/maintenance (Fig. 6a). The recess was filled with a wedge-shaped hard scale salt deposit (matched approximately to CaCO3) analyzed by means of energy dispersive x-ray spectrometry (EDS), see Fig. 6b, c and d. Selected area elemental analysis indicated severe and relatively uniform surface contamination resulted from hard scale deposits (carbonate related) that might address shaft journal cooling and operation issues. No other structural abnormality or foreign body inclusion that could be connected to the failure was identified during the fractographic study.

Fig. 6
figure 6

(a) Optical stereomicrograph of the fatigue origin showing the presence of localized dent contaminated with salt deposit; (b) SEM micrograph showing the fatigue origin at higher magnification and (c) details of boxed area are presented in (b); (d) EDS spectrum performed on the salt deposit found on fatigue origin area

Full size image

Fracture Mechanics Calculations

The presence of surface or internal flaws, such as machining marks, dents, metallurgical discontinuities, i.e., inclusions, corrosion pits, etc., constituted rather prominent sources for fatigue crack growth. Using the assumptions for short fatigue cracks emanating from small surface defects, addressed in Ref. [11] and referred in the textbook of Ref. [12], the following expression can be applied, utilizing the mean surface hardness of the material (the expression is used for hardness range: 70 < HV < 720):

$$\sigma_{\text{r,th}} = 2.86 \cdot \left( {{\text{HV}} + 120} \right) \cdot \left( {\sqrt A } \right)^{ - 1/6} \cdot \left( {\frac{1 - R}{2}} \right)^{{\left( {0.226 + 10^{ - 4} \cdot {\text{HV}}} \right)}},$$
(1)

where \(\sigma_{\text{r,th}}\)is the threshold stress range (MPa) = σ max − σ min = 2.σ a ; σ a is the  alternating stress (stress amplitude) (MPa); HV is the Vickers indentation hardness (377 HV); A is the defect projection area normal to the maximum stress (μm2); R is the stress ratio (for pure tensile stress regime, σ min = 0, R = 0).

From Eq 1, the critical threshold stress range which can give rise to fatigue crack growth from the observed surface defect of semi-elliptical shape (α = 100 μm, c = 25 μm) is deduced (Fig. 7):

Fig. 7
figure 7

Simple schematic of the geometry of semi-elliptical surface defect on the shaft’s circumference

Full size image
$$\sigma_{\text{r,th}} = \sigma_{ \hbox{max} } \approx \, 590{\text{ MPa}}$$
(2)
$$\sigma_{a} \approx \, 295{\text{ MPa}}$$
(3)

This value of stress range (\(\sigma_{\text{r,th}}\)) equals to the threshold tensile stress, over which a fatigue crack growth could be potentially induced from such surface discontinuity (Eqs 1–3).

For completely reversed stress conditions (R = −1, i.e., σ min = −σ max), the threshold stress range (\(\sigma_{\text{r,th}}\)) is calculated up to approximately 710 MPa which corresponds to stress amplitude (σ a) up to 355 MPa, signifying that minimum positive (tensile) stress above which fatigue failure occurs is almost 30% of the tensile strength. In this case, stress amplitude coincides to maximum applied stress during load cycling.

Conclusions and Recommended Actions

The investigation findings suggest strongly that the propeller shaft failed due to fatigue caused by combined rotating bending/torsional loading. Fatigue crack initiated from the shaft circumference close to the keyway area. The formation of surface conditions (flaws such as scoring lines or other wear related marks on the shaft journal) during service should be carefully checked since they constitute stress raisers, acting as potential centers for fatigue crack initiation. The presence of a surface defect of semi-elliptical shape allows the propagation of fatigue cracks for applied tensile stress threshold above 590 MPa for R = 0. Completely reversed stress conditions (R = −1) lead to a threshold alternating stress (~355 MPa) of the order of 30% approximately of the anticipated tensile strength.

Potential corrective actions to minimize the recurrence of the failures could be based on:

  1. 1.

    System prognostics: Inspection for potential excessive clearance and shaft misalignment could be proposed at the commissioning and installation stage. The option of proper analysis of system kinematics for resonant vibration frequencies could be further investigated. Moreover, the evaluation of residual stress level could be also a useful indicator for fatigue life assessment.

  2. 2.

    NDT evaluation: The implementation of periodic non-destructive inspection (such as visual inspection, dye penetrant, ultrasonic testing, etc.) of engine components during ship's scheduled maintenance is suggested to be implemented as standard procedure for future failure prevention.