Abstract
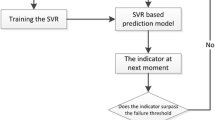
Effective degradation indicator and robust prediction model are very important for residual life prediction. Thus a new residual life prediction based on Markov indicator and support vector is proposed. Since the Markov model is good at dealing with stochastic characteristics in time domain, Markov model is joined with multiple fault features for the construction of an effective degradation indicator of rolling element bearings. The support vector regression is used to construct an adaptive prediction model composed of two prediction models that are, respectively, based on historical data and online data. Thus the ultimate prediction result is obtained by taking a weighted average of the two prediction results captured by the two prediction models, and the weights are adjusted by the LMS to enhance the prediction accuracy. The experimental results show that the Markov indicator is more sensitive than the common features, and the proposed prediction method is more effective in comparison to other methods.



















Similar content being viewed by others
References
H. Qiu, J. Lee, J. Lin et al., Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 17(3), 127–140 (2003)
J. Yan, C. Guo, X. Wang, A dynamic multi-scale Markov model based methodology for remaining life prediction. Mech. Syst. Signal Process. 25(4), 1364–1376 (2011)
J. Yu, Bearing performance degradation assessment using locality preserving projections and Gaussian mixture models. Mech. Syst. Signal Process. 25(7), 2573–2588 (2011)
J.B. Yu, Bearing performance degradation assessment using locality preserving projections. Expert Syst. Appl. 38(6), 7440–7450 (2011)
L. Liao, Discovering prognostic features using genetic programming in remaining useful life prediction. IEEE Trans. Ind. Electron. 61(5), 2464–2472 (2014)
C. Chen, G. Vachtsevanos, M.E. Orchard, Machine residual useful life prediction: An integrated adaptive neuro-fuzzy and high-order particle filtering approach. Mech. Syst. Signal Process. 28, 597–607 (2012)
Z. Tian, An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring. J. Intell. Manuf. 23(2), 227–237 (2012)
P.Y. Chao, Y.D. Hwang, An improved neural network model for the prediction of cutting tool life. J. Intell. Manuf. 8(2), 107–115 (1997)
N.Z. Gebraeel, M.A. Lawley, R. Li et al., Residual-life distributions from component degradation signals: a Bayesian approach. IIE Trans. 37(6), 543–557 (2005)
J.P. Kharoufeh, S.M. Cox, Stochastic models for degradation-based reliability. IIE Trans. 37(6), 533–542 (2005)
J.P. Kharoufeh, D.G. Mixon, On a Markov-modulated shock and wear process. Naval Res. Logist. (NRL) 56(6), 563–576 (2009)
Orchard M E. AParticle filtering-based framework for on-line fault diagnosis and failure prognosis. Georgia Institute of Technology, 2007
P. Baraldi, M. Compare, S. Sauco et al., Ensemble neural network-based particle filtering for prognostics. Mech. Syst. Signal Process. 41(1), 288–300 (2013)
M.S. Arulampalam, S. Maskell, N. Gordon et al., A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Sig. Process. 50(2), 174–188 (2002)
J.M. Lee, S.J. Kim, Y. Hwang et al., Diagnosis of mechanical fault signals using continuous hidden Markov model. J. Sound Vib. 276(3), 1065–1080 (2004)
S. Zhou, J. Zhang, S. Wang, Fault diagnosis in industrial processes using principal component analysis and hidden Markov model[C]//American Control Conference. Proc. 2004 IEEE 2004(6), 5680–5685 (2004)
B.S. Yang, A. Widodo, Support vector machine for machine fault diagnosis and prognosis. J. Syst. Des. Dyn. 2, 12–23 (2008)
T. Benkedjouh, K. Medjaher, N. Zerhouni et al., Remaining useful life estimation based on nonlinear feature reduction and support vector regression. Eng. Appl. Artif. Intell. 26(7), 1751–1760 (2013)
R.I.A. Davis, B.C. Lovell, Comparing and evaluating HMM ensemble training algorithms using train and test and condition number criteria. Formal Pattern Anal. Appl. 6(4), 327–335 (2004)
D. Basak, S. Pal, D.C. Patranabis, Support vector regression. Neural Inf. Process. Lett. Rev. 11(10), 203–224 (2007)
Acknowledgments
The work described in this paper was supported by a grant from the National Defence Researching Fund (No. 9140A27020413JB11076).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, S., Zhang, Y. & Zhu, D. Residual Life Prediction for Rolling Element Bearings Based on an Effective Degradation Indicator. J Fail. Anal. and Preven. 15, 722–729 (2015). https://doi.org/10.1007/s11668-015-0003-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11668-015-0003-z