Introduction

The ironmaking blast furnace (BF) is one of the most important but complex industrial reactors. In this process, coke, as the main fuel and reducing agent in BF ironmaking, together with iron ore are charged in alternate layers through a rotating charging chute from furnace top, resulting in a layer-structured coke and ore burden distribution. The burden will then descend slowly and affect furnace performance predominantly, including gas flow pattern, temperature distribution and species distribution of various phases. However, ironmaking BF is facing many new challenges, including decreased quality of raw materials, leading to lowered permeability, increased pressure drop and worse BF stability, and increased social pressure of environmental protection. Many innovative operations have been adopted in modern ironmaking BFs for improving BF stability and efficiency, for example, oxygen-enriched blast,[1,2] pulverized coal injection,[3,4,5,6] and central coke charging (CCC) operations.[7,8,9,10] In the process, modeling has played an important role in the investigation and optimization of BF internal states.[11,12,13,14,15,16,17]

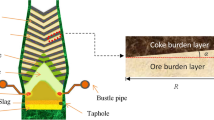
CCC operation is an efficient and flexible way to maintain stable operation. This is particularly true when the resources and supply of high-quality raw materials of coke become limited. For example, CCC operation can better tolerate the side-effects of quality fluctuations in raw materials on BF smelting process in practice.[7,18,19,20] A schematic diagram of burden layers of the CCC operation is shown in Figure 1. In the design of CCC operation, a high percentage of coke is charged at the BF central region, forming a central coke column. As a result, BF reducing gas generated inside the raceway tends to flow towards the furnace center rather than cutting across the periphery regions, leading to a relatively robust central gas stream. There are many benefits to have a robust central gas flow in the BF smelting practice by simple reasoning, which can be summarized as follows. First, the amount of heat and chemical reactants needed at the furnace center can be transferred via gas flow much easily, and thus iron oxides accumulation in the hearth center can be avoided; second, it is beneficial for BF shaft wall protection and campaign prolongation because of the decreased hot gas flush and chemical corrosion on the refractory; thirdly, zinc and other alkali elements which deteriorate BF smelting performance and BF wall refractory can be discharged much easily with a relatively strong central gas flow; fourthly, coke abrasion at the furnace center can be suppressed, which promote the hot metal and slag penetration through the stagnant region (deadman), and help to reduce the circular flow of liquid metal near the hearth wall; lastly, increased coal injection rate is expected since central gas development can offset coal particle accumulations and their blocking effects on gaseous phase flow. Nevertheless, as reported in the literature,[9,10,21,22] CCC operation also has some drawbacks in some cases; for example, lowered gas utilization efficiency and increased fuel rate, and the over-developed central gas might lead to a waste of valuable thermochemical substances and energy. The reasons behind these phenomena are complex but mainly due to the lack of the systematic understanding of this operation. Moreover, these reasoning and hypotheses of CCC operation, including benefits and drawbacks have not been well characterized quantitatively since detailed in-furnace phenomena are hard to measure in practice.

Fig. 1
figure 1

Schematic of sectional views of BF under the CCC operation: (a) top view and (b) front view near the further top

Full size image

The CCC operation has been studied using plant test and mathematical models. For example, Toshiyuki et al. reported the effectiveness of the CCC operation in a commercial BF in Japan.[7] Wang reported the influence of CCC operation on the smelting practice of iron-fluorine bearing ore.[19] Feng reported a case in which the CCC operation was successfully used to improve the activity of BF central regions.[23] It was found that CCC operation can indeed increase the permeability of gas and liquid flow, stabilize BF operation and help to improve the coal injection rate and furnace performance. However, BF is a huge black box, and more detailed phenomena under the CCC operation cannot be directly indicated or measured in practice. Therefore, the mathematical modeling approach has been used for understanding CCC operation. For example, Kiichi et al. studied the behavior of charged burden concerning the formation of a central coke column.[24] It was found that the CCC operation has little influence on gas flow in BF lower parts. Their work was based on aerodynamics analysis and no thermal–chemical phenomenon was considered. Teng et al. studied the relationship between the CCC operation and top gas utilization efficiency considering the gas flow resistance inside a BF.[25] However, the structure of solid bed was simplified to a large degree and in-furnace thermal–chemical behaviors were not considered in their work. To the best of our knowledge, so far, few CCC modeling works concerning multi-phase flow and quantified thermal–chemical distributions has been systematically reported in the open literature.

In this paper, a recent BF mathematical model[26] based on multi-fluid theory is further developed to study the inner phenomena of a BF under CCC operation, where respective thermochemical behaviors are considered in the coke and ore layers. Then, the typical internal states, including flow patterns, thermal–chemical behavior, reducing gas evolution and ferrous oxide distribution are investigated systematically and quantitatively, and compared with the non-CCC operation where necessary. This work might provide an insight into the fundamentals of CCC operation.

Model Description

The present model is based on a recent multi-fluid BF model, which has been validated by comparing the top gas information with those measured in BF ironmaking practice.[26] In the recent model, one important feature is the consideration of chemical reactions in respective coke- and ore- layers, compared to the previous BF models in the literature. In this paper, the recent model is further developed considering the specific burden profiles of CCC operation and used to investigate the related BF performance. In this part, the governing equations and expressions such as the interphase momentum transfer and chemical reaction rates are not included here for brevity. The model basics and new developments are introduced here for completeness.

Model Basics

The model is in 2-D of axial symmetry. The calculation domain of the BF model ranges from slag surface in the furnace hearth up to the stockline level at the furnace throat. It includes gas–solid–liquid flows, interphase momentum interaction and heat transfer, and main chemical reactions. Navier–Stokes equations are used to describe the solid and gas flows.[27,28,29,30,31,32,33,34,35,36,37] A force balance model[38] is used to simulate liquid flow considering gas–liquid and solid–liquid interactions. Regarding the phase momentum transfer, an Ergun-type equation[39] is adopted to simulate the momentum exchange between gas and solid phases. The following models are used to model the interphase heat exchange between different phases: a modified Ranz–Marshell model for gas–solid phases,[40] Eckert–Drake equation for solid–liquid phases,[41] Mackey–Warner equation for gas–liquid iron phases[42] and Maldonado method for gas–slag phases.[43] In this model, the layered structures of solid coke and ore burden and the corresponding physical, thermal, and chemical properties in adjacent coke and ore layers are explicitly considered.[26] Notably, as coke and ore are charged alternately from the furnace top, coke and ore particles remain in their own layers in the shaft regions to a large degree and the chemical reactions related to iron oxides should only take place in the ore layers while the reactions related to coke particles such as carbon solution-loss and water–gas reaction should happen only in the coke layers. The chemical reaction rate of iron-bearing ore reduction by CO and H2 is based on Muchi’s paper.[44] Specifically, the reaction model assumes that three steps including diffusion through gas film, intraparticle diffusion and chemical reaction on the reaction interface occur steadily and successively during reaction. In the expression, chemical equilibrium constant is used to derive the ‘driving force’ (specie concentration under equilibrium state minus specie concentration under local state) for chemical reactions. Note that the value of chemical equilibrium constant varies with temperature. The reaction rate provides the basis for mass sources or sinks calculation for N-S equation and scalars’ (the mass fractions of CO, H2, CO2 and H2O) equations. The two boundary profiles of cohesive zone are naturally determined by the solid temperature range of 1473 K to 1673 K based on the simulation results.[30,33,34] In this study, the shrinkage ratio (Sh) is used to represent the softening and melting status of iron-bearing materials. It is a function of solid temperature. As such, the cohesive process and Shrinking Index are calculated in three states according to the shrinkage ratio[30]:

  1. (a)

    State I (Shrinking Index equals to 1), 0.7 < Sh < 1.0 corresponded to the portion with molten state and liquid source in which the ore layer voidage is occupied fully by the liquid phase.

  2. (b)

    State II (Shrinking Index equals to 2), 0.5 < Sh < 0.7 corresponded to the combined portion with softening and melting of ore particles.

  3. (c)

    State III (Shrinking Index equals to 3), 0.0 < Sh < 0.5 corresponded to the softening stage in which the ore-melting process is limited.

In each state, different particle size and porosity are set.[30] In addition, gas phase is assumed as an incompressible fluid in this study, as its velocity in most regions of BF is relatively low. Finally, both the variation of cohesive zone position[33,34] and top gas utilization efficiency are adopted as the convergence criteria. The expression of the latter criterion can be expressed as follows:

$$ \sqrt {{{\sum\limits_{i - n + 1}^{i} {\left( {\chi_{i} - {{\sum\limits_{i - n + 1}^{i} {\chi_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{i - n + 1}^{i} {\chi_{i} } } n}} \right. \kern-0pt} n}} \right)^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{i - n + 1}^{i} {\left( {\chi_{i} - {{\sum\limits_{i - n + 1}^{i} {\chi_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{i - n + 1}^{i} {\chi_{i} } } n}} \right. \kern-0pt} n}} \right)^{2} } } n}} \right. \kern-0pt} n}} \le \bar{\varepsilon } $$
(1)

where, χi is the CO utilization and/or H2 utilization of top gas while i, n and \( \bar{\varepsilon } \) are the index of top gas utilization data, count number of top gas utilization data and the convergence criteria, respectively.

New Developments for CCC Operation

Different from normal charging pattern, in CCC operation, only or excessive coke particles are charged to the furnace center, forming a central coke column, while coke and ore are charged in alternate layers in other regions. To quantify the effects of CCC operation on furnace performance, the layered structure of CCC operation is characterized before the simulation. In this model, the distribution of coke layers and ore burden layers are characterized as shown in Figure 2. The solid layer distribution can be calculated using the timeline of solid flow as described in a Reference 26. Here, the advantage of the previous layer-structured model is used to solve the particle distributions inside BF adopting CCC operation. The equations listed below are derived and then used to calculate the primary parameters of top coke and ore layers.

Fig. 2
figure 2

Structure of burden under the CCC operation in this study

Full size image
$$ V_{\text{coke}}^{*} = R^{2} \left( {H - h_{2} } \right) + L_{0}^{2} h_{2} + {{L_{0} h_{2}^{2} } \mathord{\left/ {\vphantom {{L_{0} h_{2}^{2} } {tg\alpha }}} \right. \kern-0pt} {tg\alpha }} + {{h_{2}^{3} } \mathord{\left/ {\vphantom {{h_{2}^{3} } {\left( {2tg^{2} \alpha } \right)}}} \right. \kern-0pt} {\left( {2tg^{2} \alpha } \right)}} $$
(2)
$$ V_{\text{burden}}^{*} = \left( {R^{2} - L_{0}^{2} } \right)h_{2} - {{L_{0} h_{2}^{2} } \mathord{\left/ {\vphantom {{L_{0} h_{2}^{2} } {tg\alpha }}} \right. \kern-0pt} {tg\alpha }} - {{h_{2}^{3} } \mathord{\left/ {\vphantom {{h_{2}^{3} } {\left( {2tg^{2} \alpha } \right)}}} \right. \kern-0pt} {\left( {2tg^{2} \alpha } \right)}} $$
(3)
$$ V_{\text{coke}}^{ *} = {{M_{\text{coke}} } \mathord{\left/ {\vphantom {{M_{\text{coke}} } {\left( {\pi \rho_{\text{coke}} } \right)}}} \right. \kern-0pt} {\left( {\pi \rho_{\text{coke}} } \right)}} $$
(4)
$$ V_{\text{burden}}^{*} = {{M_{\text{burden}} } \mathord{\left/ {\vphantom {{M_{\text{burden}} } {\left( {\pi \rho_{\text{burden}} } \right)}}} \right. \kern-0pt} {\left( {\pi \rho_{\text{burden}} } \right)}} $$
(5)
$$ R = L_{0} + L_{1} + L_{2} $$
(6)

where R is radius of furnace throat, L0 is the CCC column width, α is the repose angle of coke pile, \( V_{\text{coke}}^{ *} \), \( V_{\text{burden}}^{*} \), Mcoke, Mburden,ρcoke and ρburden are scale-down coke volume, scale-down burden volume, coke batch weight, ore burden batch weight, bulk density of coke, bulk density of ore, respectively. Once the values of the basic parameters mentioned above are determined, the volume fractions of coke and ore can be exclusively derived. Then they can be used as the boundary conditions of solid flow and subsequent simulations. This approach can be considered useful to capture the main features of burden distribution in the CCC operation, especially when used to investigate the influence of central coke region on BF performance quantitatively.

Simulation Conditions

The schematic of the computational domain and mesh is shown as in Figure 3. In this simulation, the radius of central coke (~ 0.35 m) is one-sixteenth of the furnace throat radius, which is in the typical range of CCC operation practice. The inclined angle of the coke pile is set to 0.524 radians based on the repose angle of coke pile. The porosity of both coke and ore layers are calculated based on the empirical formulae widely used in BF modeling studies.[45] Particle size affects the porosities of coke and ore, and thus it affects the bulk densities of coke and ore and the respective burden profiles. In this study, the ore particle size is set to a constant (0.03 m) while the coke particle size follows a decreasing linear relationship with the increased furnace radius (0.06 m at furnace center and 0.03 m at furnace wall). However, for the bulk density calculation in the CCC profile model, the average sizes of particles (0.03 m and 0.045 m for ore and coke particles, respectively) are adopted for simplicity. The initial distributions of particle size and porosity inside a BF are extracted from furnace top, which will provide the standard value for those properties in different regions for the calculations. For comparison, both CCC and non-CCC cases are set to the same gas inlet boundary conditions including flame temperature, reducing gas components and bosh gas flow rate. The burden profile of non-CCC operation is referred to previous work.[34] The simulation conditions are set based on the operational data of a commercial BF (Table I).

Fig. 3
figure 3

The calculation domain (a) and section mesh (b) of this model

Full size image
Table I Simulation Conditions of this Model
Full size table

Results and Discussion

In this section, the in-furnace phenomena with and without CCC operation (in which both coke and ore are charged into the furnace central regions) are compared, in terms of flow fields, temperature fields, species distributions and chemical reactions. Moreover, the CCC simulation results using this model are also compared with results using the CCC model without considering chemical reaction switch between coke and ore layers.

Comparison of CCC Operation with Non-CCC Operation

Gas flow

Figure 4 compares the quantitative results of gas velocity field, porosity distribution, gas density and gas flow pattern in the BF, respectively, under the CCC operation vs non-CCC operation. Figure 4(a) confirms that the reducing gas bears a relatively high velocity at BF central regions and forms a distinct high-gas volume fraction region (i.e. gas column) under the CCC operation compared to that of non-CCC operation (Figure 4(b)). The central gas column is mainly caused by the higher porosity distribution (Figure 4(c)) at the center. Robust central gas is regarded as helpful to protect hearth and shaft wall from hot gas flush. The region with low gas density, which usually exists at the lower regions, can have a larger area under the CCC operation, as shown in Figure 4(d). BF gas density results from thermal-pressurized conditions and appears in Navier–Stokes equations. To ensure mass balance, low-density regions such as BF central regions should have high velocity. Figure 4(e) presents the gas streamline when adopting the CCC operation. It is seen that the reducing gas can easily pass through the thin and narrow cohesive layers near the furnace center, but is significantly redirected by the ‘coke windows’ at the peripheral regions. Besides, it is found that the cohesive zone top opening radius is around 0.50 m, larger than the CCC radius (~ 0.35 m) at furnace top, as seen from Figures 4(c) and (e), indicating less liquid generated at BF central regions. The results are based on flow-thermal-chemical calculation and provide the basis for understanding the inner phenomena of CCC operation.

Fig. 4
figure 4

Typical results of flow pattern in the BF: (a) gas velocity field in the CCC case; (b) gas velocity field in the non-CCC case; (c) porosity distribution in the CCC case; (d) gas density distribution in the CCC case and (e) gas streamlines around the cohesive zone in the CCC case

Full size image

Thermal behaviors

Figure 5 shows the temperature fields of gas and solid phases and the temperature difference between gas–solid phases (termed D value), respectively. Due to the counter-current conditions and endothermic chemical reactions such as direct reduction of wustite, the isotherms of the solid always are located below those of the gas phase. Though CCC operation has a distinct impact on rising the temperature of both gas and solid phases at central regions, it is found that their isotherms become quite congested in the horizontal direction. This is because the adjacent ore particles require more thermal energy to heat. Thus, the driving force for heat exchange, namely, temperature difference, becomes quite large in the horizontal direction. Figure 5(c) presents how temperature difference (D value) evolves under CCC operation. The isotherms and corresponding labels are indicated for gas phase for comparisons. Under the CCC operation, the region of large D value expands to a much higher area near furnace center, which is driven by the strong central gas flow. The thermal conditions at BF center promote iron oxides to melt and be reduced earlier and faster, and thus the accumulation of iron oxides in hearth center can be avoided in CCC operation.

Fig. 5
figure 5

Temperature fields under the CCC operation: (a) gas phase temperature; (b) solid phase temperature and (c) temperature difference (D-value) between gas and solid phases

Full size image

Top gas temperature is considered as an important index to judge furnace performance, and is widely used to estimate gas flow patterns and energy utilization efficiency.[46,47,48] Figure 6 shows the top gas temperature distribution along the radial direction under the CCC operation. Overall, the curve shows a bell-shaped pattern. It is seen that the temperature distribution curve drops fast with the increasing radius and then attains a plateau with unobvious variations near BF wall. At furnace center, the top gas temperature of the CCC operation is found to be ~ 1000 K though these high-temperature regions are quite narrow. In practice, high temperature of top gas might be a threat to the dust-collection systems that follows and thus should be well controlled. Besides, the CCC operation has a higher average top gas temperature (~ 270 °C) than that of the non-CCC operation (~ 252 °C), indicating CCC operation might face with high-fuel rate.

Fig. 6
figure 6

Top gas temperature profile along the radial direction under CCC operation

Full size image

Figure 7 compares the inner thermal phenomena between the CCC and non-CCC operations quantitatively where the isotherms for non-CCC operation are colored in light purple for contrast. Figure 7(a) shows the isotherms of 1473 K and 1673 K in solid phase, which defines the boundary of cohesive zones. In CCC operation, the temperature range to define cohesive zone extends to a greater height at the central region than non-CCC operation, however, a relatively lower height of the cohesive zone is observed at the peripheral regions. From Figures 7(b) and (c), it is indicated that near furnace central regions, the isotherms for the CCC operation are much steeper (~ 80 deg) compared to the non-CCC operation (~ 60 deg), indicating that the heat load is quite different in these two operations. Particularly, CCC operation has a lighter heat load at peripheral regions, especially in shaft. This explains why CCC operation can protect shaft refractory. Besides, the temperature range of 1200 K to 1400 K in solid phase is generally considered as the thermal reserve zone (TRZ) where mainly the indirect reduction of wustite takes place. It can be seen that the TRZ shifts to the peripheral regions in the CCC operation while TRZ has larger areas near BF center in non-CCC case. TRZ shrinks indicates the region for indirect reduction shrinks. Thus, it is supposed that fuel rate in CCC tends to increase.

Fig.7
figure 7

Thermal state comparisons of the CCC and non-CCC operations: (a) the temperature range of cohesive zone; (b) isotherms of gas phase and (c) isotherms of solid phase

Full size image

Distributions of gas and solid species

Figure 8 shows the molar fractions of each of the components CO, CO2, H2, H2O and N2 in the reducing gas, and CO gas utilization efficiency of the CCC operation. Readers may refer to our previous works for comparison[26] with the non-CCC operation. The concentration isotherms of gas components (Figures 8(a) to (d)) show trends of fluctuations (zig–zag) except in the case of N2 (Figure 8(e)). This is because coke and ore layers function as different mass sources/sinks for CO, CO2, H2 and H2O, however, there is no mass source/sink associated with N2 in this BF model. Besides, it is proved that CCC operation makes gas components, such as CO and H2, flow through BF center more easily. Thus, CO utilization efficiency is lowered at BF central regions, as shown in Figure 8(f).

Fig. 8
figure 8

Contours of variables for the gas phase in the CCC operation: (a) molar fraction of CO; (b) molar fraction of CO2; (c) molar fraction of H2; (d) molar fraction of H2O; (e) molar fraction of N2 and (f) gas utilization efficiency

Full size image

To further study the reducing gas distributions in the CCC operation, the molar fractions of CO and CO2 in top gas are plotted as a function of the furnace radius, as shown in Figure 9. It is seen that the distribution curves of CO and CO2 form a hopper-like shape, namely, the two distribution curves show the opposite trends, with roughly 40 pct (CO) and 2 pct (CO2) at the furnace center, and 23 pct (CO) and 22 pct (CO2) in the position of about half BF throat radius, after which the variations up to the furnace wall are insignificant. For a better comparison, the average concentrations of CO and CO2 in the top gas in the cases of CCC and non-CCC operations are also calculated. It shows that the CCC operation has a larger average concentration level of CO (~ 27 pct) while a smaller concentration level of CO2 (~ 20 pct) compared to the case of non-CCC operation (~ 22 pct CO and ~ 22 pct CO2).

Fig. 9
figure 9

Molar fractions of CO and CO2 along the radial direction at top surface in the CCC study

Full size image

Figure 10 shows the CO utilization efficiency of top gas as a function of furnace radius under the CCC operation. It is indicated that the gas efficiency distribution curve bears an inverse-bell-shape trend. It starts from its valley at the furnace center, increases gradually along throat radius, and then arrives at a plateau roughly at the utilization efficiency of 50 pct at about half throat radius. Finally, the curve slightly drops off towards the wall. This indicates that the reducing gas is not adequately utilized in and around the furnace center than near the peripheral regions. This is because in CCC operation, BF center is only occupied by coke where no iron oxides reduction can take place. Thus, CO in central gas cannot be utilized well. On the other hand, measurable amounts of ore particles exist at the peripheral regions, and therefore, CO has more chance to participate in iron oxides reductions and can be relatively utilized better. The average top gas utilization efficiency and predicted coke rate of both CCC and non-CCC cases are also compared. It shows that the CCC operation has a relatively lower average top gas utilization efficiency (~ 43 pct) compared to the non-CCC operation (~ 50 pct). Besides, a relatively higher coke rate (~ 348 kg/tHM) is predicted in the CCC operation than non-CCC operation (~ 343 kg/tHM). Note that due to model limitations, coal rate is fixed in this study. Thus, carbon rate increase can only be reimbursed by coke rate increase. However, as stated before, if more coal were injected, coke usage would be saved.

Fig. 10
figure 10

Top gas utilization along the radial direction at furnace top under CCC operation

Full size image

Figures 11(a) to (e) show the distributions of solid species including hematite, magnetite, wustite, metal iron and reduction degree under the CCC operation. The isotherms here are solid temperature. From Figure 11(a), it can be seen that the mass fraction level of hematite is stable near BF stockline, but it shows a sharp decrease in the temperature range of 600 K to 800 K. This distribution is similar to that of non-CCC case,[26] but its area is larger because the thermal loads of CCC case are relatively lighter in the peripheral regions. On the other hand, magnetite (Figure 11(b)) is produced from the further reduction of hematite and its peak is roughly attained at 900 K with the vanishing of hematite. Then, a chemical reserve zone (CRZ) of magnetite is formed, until thermal–chemical conditions for further reduction are reached. However, the CRZ profile of magnetite locates lower and it is in a more rectangular-like shape compared with that of non-CCC case.[26] For wustite distribution, however, it is found that the wustite CRZ in CCC operation is narrower than that of non-CCC case. The different thermal patterns should be the major reason. The contours confirm that CRZs and metal iron (Figure 11(d)) exist except at BF central regions which are consistent with reasoning.

Fig. 11
figure 11

Contours of variables for the solid phase in the CCC operation: (a) hematite mass fraction; (b) magnetite mass fraction; (c) wustite mass fraction; (d) metal iron mass fraction and (e) reduction degree of ferrous oxides above dripping zone

Full size image

Figure 11(e) shows the distribution of ferrous oxides reduction degree which was calculated based on:

$$ R_{\text{ore}} = 1 - \frac{2}{3}\frac{{n_{\text{O}} }}{{n_{\text{Fe}} }} $$
(7)

where no is the moles of oxygen element in ore, while nFe is the moles of iron element in ore. It is seen that the reduction degree shows a gradual increase in the regions from the top burden surface to the cohesive zone while it remains relatively stable in each CRZ. The reducing gas concentrations also remain relatively stable in each CRZ, as can be seen from Figure 8. Moreover, it is observed that iron oxides at BF central regions can be reduced earlier than in peripheral regions. Thus, the reduction loads of CCC in BF central-lower parts are lessened. This helps to explain why CCC operation can have an active hearth.

Carbon solution-loss reaction

The carbon solution-loss reaction (C + CO2 → 2CO) is an important reaction in BF ironmaking. The more coke reacts via this reaction, the larger chance coke becomes small size coke, even coke powder. As a result, permeability inside BF becomes worse. Comparing Figures 12(a) with (b), it can be seen clearly that in CCC operation, carbon solution-loss reaction shifts from BF center to peripheral regions. For better comparisons, the average carbon solution-loss reaction rate as a function of furnace radius in each case is shown in Figure 12(c). To calculate the average reaction rate, BF domain is evenly divided into 40 sections while each section locates in a range of radii. Then, the average reaction rate is calculated based on:

$$ \overline{\eta } = {{\sum\limits_{i}^{N} {\eta_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{i}^{N} {\eta_{i} } } N}} \right. \kern-0pt} N} $$
(8)

where \( \eta_{i} \) is reaction rate in the ith coke cell and N is the number of coke cell in the section. From Figure 12(c), it is seen that the average carbon solution-loss reaction rate in the CCC case is always lower than the non-CCC case, by roughly 92 pct in the center and 18 pct near furnace wall, indicating that the carbon solution-loss reaction rate can be effectively decreased in CCC operation. Thus, the risk of coke degradation inside a BF can be reduced, especially at BF central regions. Therefore, a good permeability and stable performance of BF can be ensured.

Fig. 12
figure 12

Carbon solution-loss reaction rate: (a) of the CCC operation; (b) of non-CCC operation and (c) along the radial direction

Full size image

Comparison of Simulation Results Using Two CCC Models

Although coke and burden are charged alternately, BF models usually treats them as a mixture and set chemical reactions occur non-selectively inside coke and ore layers. Figure 13 shows the representative results of CCC case without considering chemical reaction switch between coke and burden layers (henceforth referred to as CCC-2). Comparing Figures 13(a) to (c) with Figures 8, it is seen that the whole trends of the contours are similar. However, the fluctuation (zig–zag) trends of the isotherms cannot be observed in CCC-2. When comparing Figures 13(d) and (e) with Figures 11(e) and 12(a), it is observed that the indices show similar trends but have quantitative differences. Particularly, CCC-2 has a lower CO concentration (36.5 pct) at BF center and a higher CO2 concentration (23 pct) near peripheral regions (Figure 13(f)), and thus a higher CO gas utilization efficiency is predicted (Figure 13(g)).

Fig. 13
figure 13

Representative results of CCC-2: (a) CO molar fraction; (b) CO2 molar fraction; (c) reducing gas utilization; (d) iron oxides reduction degree (note: the isotherms are indicated for solid temperature (K)); (e) carbon solution-loss reaction rate; (f) molar fractions of CO and CO2 along the radial direction at top surface and (g) top gas utilization along the radial direction at furnace top

Full size image

This BF model considers “respective reacting layers” where different chemical reactions are considered in coke and ore layers, respectively,[26] by contrast to the BF models where a “mixture” of coke and ore burden was simply considered and thus did not consider the different chemical reactions in the respective layers of ore and coke. The former method is more realistic as the chemical reactions occurring in coke and ore layers are different in BF practice. Thus, phase concentration should show fluctuating or zig-zag profiles. However, if a mixture model is used, this feature cannot be captured.

Conclusions

A 2-D axisymmetric multi-fluid BF model is extended for investigating CCC operation. This model features the respective chemical reactions in respective coke and ore layers, and a sub-model of layer profile for the burden structure for CCC operation. The multi-phase flow and thermochemical in-furnace phenomena of CCC operation can be comprehensively simulated and quantitatively compared with the results of non-CCC operation. The key findings of this CCC operation are summarized as follows:

  1. 1.

    Both gas permeability and cohesive zone position are high at BF central regions. In this given case, when CCC opening at the throat is 0.35 m, cohesive zone top opening is around 0.50 m.

  2. 2.

    The temperature curve of top gas shows a bell-shape trend with a narrow region of high temperature, close to 1000 K at the furnace center. In addition, the isotherms of CCC operation become much steeper (~ 80 deg) than those of non-CCC operation (~ 60 deg).

  3. 3.

    It is found that the reducing gas utilization efficiency declines from ~ 50 to ~ 43 pct. Also, CRZ profiles of iron oxides are quite different from those of non-CCC operation. Besides, CCC operation faces with fuel rate increase though it can stabilize BF performance.

  4. 4.

    It shows that carbon solution-loss reaction rate can be effectively suppressed at the furnace center by ~ 92 pct. This confirms the objective of good permeability at BF central regions using CCC operation.

This model has provided a cost-effective way to systematically investigate CCC operation. This model is relatively high in calculation efficiency and is feasible to study the influence of, such as CCC opening radius, batch weight and furnace throat radius on BF performance. However, the detailed flow behavior at particle scale, such as particle percolation, friction and segregation cannot be captured. A large-scale DEM-CFD simulation is a promising method to capture those particle scale reacting flow phenomena but it is not computationally feasible so far considering the huge particle number in BF operations.