Introduction

The reduction of iron ore fines by means of fluidized bed technology has been of interest to the iron and steel industries for many years to produce direct reduced iron (DRI).[1] In the near future, the importance of DRI will increase drastically. Overall steel production has risen about 100 pc. over the past 20 years, from 0.85 to 1.7 billion tons of crude steel.[2] Consequently, the scrap return will also increase within the next few years, considering the fact that a typical life cycle time of steel products is 25 years. Thus, the amount of steel produced via the process route based on an electric arc furnace (EAF) will also grow in the near future. To obtain high-quality steel grades, the demand for DRI will also rise as a scrap substitute in the EAF. Aside from the increasing demand, direct reduction processes have advantages over conventional steel making via blast furnace and oxygen converter, especially in terms of environmental issues. Some direct reduction processes are able to operate with high hydrogen content in the reducing gas mixture. Therefore, accompanying CO2 emissions can be reduced. The use of fluidized bed technology brings one further advantage, as fine iron ores can be used directly without a prior agglomeration step. Examples of direct reduction processes using fluidized bed technology in industrial scale are the Finmet®[3,4] and the Circored®[5,6] processes. Both are based on natural gas as an energy source, whereby in the case of Finmet®, the required reducing gas mixture is produced by means of the reforming of natural gas. In contrast, the Circored® process only uses hydrogen as a reducing agent, also provided by means of the reforming of natural gas in combination with a shift reactor and a CO2 removal unit.

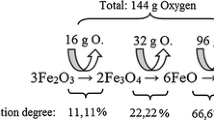
During the direct reduction of iron oxide with hydrogen at temperatures above 843 K, the reduction proceeds from hematite Fe2O3via magnetite Fe3O4 to wüstite FeO and finally to metallic iron Fe. Below 843 K, reduction occurs from magnetite directly to metallic iron, owing to wüstite not being stable below 843 K. The reactions are shown in Eqs. [1] through [4],[7] where y represents iron vacancies in the lattice. The values of ΔH, calculated with the thermodynamic software FactSageTM7.2 (Database: FactPS, FToxide), show for each reduction step that the reduction of iron oxide with hydrogen is in total endotherm, so energy is required to ensure a constant temperature during reduction. In general, reduction takes place stepwise from iron with high valence to metallic iron. It is also possible that more than one reduction step takes place similarly within different areas in the particle, especially in the case of big particles, e.g. during the reduction of lump ore.[8]

$$ \begin{aligned}3{\text{Fe}}_{2}{\text{O}}_{3} + {\text{H}}_{2} \to 2{\text{Fe}}_{3} {\text{O}}_{4} + {\text{H}}_{2} {\text{O}} \quad \Delta {\text{H}}_{{973{\text{K}}}} = - 2.17\,{\text{kJ}} \end{aligned} $$
(1)
$$ \begin{aligned}&T<843\,{\text{K}}\\&{\text{Fe}}_{3} {\text{O}}_{4} + 4{\text{H}}_{2} \to 3{\text{Fe}}+ 4{\text{H}}_{2} {\text{O}} \quad \Delta {\text{H}}_{{773{\text{K}}}} = + 111.28 \,{\text{kJ}} \end{aligned} $$
(2)
$$ \begin{aligned}&T> 843\,{\text{K}} \\ &(1 - y){\text{Fe}}_{3} {\text{O}}_{4} + (1 - 4y){\text{H}}_{2} \to 3{\text{Fe}}_{(1 - y)} {\text{O}}+ ( 1 - 4y){\text{H}}_{2} {\text{O}} \\&\quad \Delta {\text{H}}_{{973{\text{K}}}} = + 52.16 \,{\text{kJ}} \end{aligned} $$
(3)
$$\begin{aligned}&T> 843\,{\text{K}} \\&{\text{Fe}}_{(1 - y)} {\text{O}}+ {\text{H}}_{2} \to (1 - y){\text{Fe}} + {\text{H}}_{2} {\text{O}}\\ &\quad \Delta {\text{H}}_{{973{\text{K}}}} = + 15.42 \,{\text{kJ}} \end{aligned} $$
(4)

Figure 1 shows the so-called Baur–Glässner diagram for the Fe-O-H2 system, with temperature on the ordinate and the gas oxidation degree (GOD) on the abscissa. The GOD is defined as the ratio of oxidized components over the sum of oxidized and oxidizable components in the reducing gas mixture. The thermodynamic data required for the calculation was provided by FactSageTM 7.2. The diagram shows the stability areas of different iron oxides as a function of temperature and GOD. It can be seen that the stability areas of metallic iron and wüstite expand with increasing temperatures. As a result, a reducing gas mixture with a similar GOD has a higher reduction potential if the reduction temperature is higher. From a thermodynamic point of view, the temperature should be as high as possible. During fluidized bed reduction, the practical temperature is limited due to sticking of the fluidized particles that can occur. This could end in a defluidization of the material.[9,10]

Fig. 1
figure 1

Baur–Glässner diagram for the Fe-O-H2 system

Full size image

Investigations regarding the reduction kinetics of iron oxides using hydrogen as a reducing agent have been carried out by many authors.[11,12,13,14,15,16,17,18,19] The scope of this work was to investigate the reduction kinetics of iron ore fines during fluidized bed reduction using hydrogen as a reducing agent in a suitable temperature range for an industrial application. The determination of the apparent activation energy against the degree of reduction, model–fitting analysis of experimental results as well as multistep kinetic analysis were carried out. Conclusions were drawn concerning the shape of the apparent activation energy against the degree of reduction and the results from kinetic analysis.

Experimental Procedure

Experimental Setup

The schematic concept of the laboratory scale fluidized bed reactor used is shown in Figure 2. The necessary reducing gas components were stored in gas bottles and the required mixture was provided by mass flow controllers (Bronkhorst EL-Flow F201-CV/AV) in a gas mixing unit. If water vapor was required in the reducing gas mixture, the gas passed through a humidifier (Bronkhorst Evaporator W-303A-333-K), where the H2O was added to the mixture. The preheating of the reducing gas to reduction temperature took place while passed through the supply pipe inside a 3-stage electrical heating shell, where the reactor itself was also located during the experiment. The reducing gas entered the reactor from the bottom, passed the grid and fluidized the material. To remove accompanying dust from the gas, an internal cyclone and a dust filter unit were installed before the off-gas left to the atmosphere. The pressure inside the reactor was controlled by a pressure regulator (Masoneilan 28-23131), located in the off-gas duct. To evaluate the fluidization behavior, differential pressure measurements (Kobold Smart pressure transmitter) were carried out under the grid and above the material. To control the temperature of the reducing gas mixture and the sample portion, thermocouples (type N) were installed below the grid and inside the sample portion. The weight loss sustained during the reduction was measured via a scale (Mettler Toledo XP64000L), which showed the weight of the whole reactor including the material. To minimize iron ore losses, the upper part of the reactor was designed in a conical shape to reduce the superficial gas velocity. The geometrical shape and the operating conditions of the fluidized bed reactor can be summarized as follows: 68 mm bed diameter of reactor with conical shape in the gas outlet area; perforated grid with 33 orifices (1 mm in diameter); temperature up to 1373 K; absolute pressure up to 1.4 bar; sample mass up to 650 g and the reducing gas contained H2, N2 and H2O (CO, CO2 and CH4 were also possible).

Fig. 2
figure 2

Experimental setup laboratory fluidized bed reactor: 1—gas mixing unit; 2—humidifier; 3—grid; 4—internal cyclone; 5—filter unit; 6—pressure regulator; 7—differential pressure measurement; 8—weighing device; 9—reactor; 10—3-stage electrical heating shell; 11—process control; 12—off-gas to atmosphere

Full size image

Before the experiment, the iron ore sample was placed into the reactor and purged with N2 to remove oxygen from the system. The heating period to the desired reduction temperature took place under constant N2 flow. After that, a temperature-equilibrium period of 10 minutes was chosen in order to reach a stable weight signal and a constant temperature. Then, N2 was replaced by the defined reducing gas mixture and the reduction procedure started. The change in the sample weight and the differential pressure through the grid and sample portion were measured during the experiment to evaluate the reduction and fluidization behavior. After the reduction period, the reducing gas mixture was substituted by N2 again, and the sample was cooled down to ambient temperature before discharging.

Experimental Conditions

To evaluate the kinetics of the reduction of hematite iron ore by hydrogen, reduction experiments were carried out at different temperatures. The chemical analysis of the iron ore as well as the specific surface area and the general test parameters are shown in Table I. A 400-g sample portion with a grain size between 250 and 500 µm was used for each test. The reducing gas mixture consisted of 65 pc. H2 and 35 pc. N2, by volume, with a constant flow rate of 25.9 Nl min−1. N2 was added to the gas mixture to support the fluidization of the particles. A constant molar flow at different temperatures ends in different superficial gas velocities inside the reactor. As a suitable temperature range for fluidized bed reduction, 873 K to 1073 K was chosen, whereby for each 50 K, one reduction experiment was performed. At 873 K, a flow rate of 25.9 Nl min−1 represents a superficial gas velocity of 0.35 m s−1, while at 1073 K, it is 0.43 m s−1. An absolute pressure of 1.1 bar was provided to the sample portion during reduction.

Table I Chemical Analysis of Iron Ore and Process Conditions
Full size table

The measured weight change can be directly converted into the degree of reduction and metallization using the chemical analysis of the iron ore. The degree of reduction, RD, is defined as shown in Eq. [5] and the metallization, Met, as presented in Eq. [6]:

$$ RD \left[ {\text{pct}} \right] = \left( {1 - \frac{O}{{1.5 \cdot {\text{Fe}}_{\text{tot}} }}} \right) \cdot 100 $$
(5)
$$ {\text{Met}} \left[ {\text{pct}} \right] = \frac{{{\text{Fe}}_{\text{met}} }}{{{\text{Fe}}_{\text{tot}} }} \cdot 100 $$
(6)

where Fetot represents the total iron amount of the iron ore sample and O the amount of oxygen bonded on iron in mol.

To evaluate the fluidization conditions during the reduction experiments, a calculation of the Grace diagram was done. The Grace diagram shows the dimensionless gas velocity against dimensionless particle diameter. The calculation values used for the experimental conditions at 973 K are summarized in Table II. The density and viscosity of the fluid were calculated according to the proposed procedure from the VDI Heat Atlas.[20] The value for sphericity of the solids was determined experimentally by measuring the minimum fluidization velocity in comparison with the results from the calculation using the Ergun equation.

Table II Calculation Parameters of the Grace Diagram
Full size table

For the calculation of the Grace diagram, Eqs. [7] through [11] were used.[21,22,23] Equation [7] shows the Ergun equation for the determination of the minimum fluidization velocity. Equation [8] allows the calculation of the terminal velocity, whereby cD represents the Drag coefficient, which can be calculated using Eq. [9]. Rep represents the particle Reynolds number. The transformation of gas velocity and particle diameter into dimensionless numbers, as required for the Grace diagram, can be done using Eqs. [10] and [11]. The usage of dimensionless particle diameter and gas velocity is helpful because each of them includes only dp or u and properties which are constant for a given fluid–solid system. Therefore, different process conditions can be shown easily.

$$ u_{\text{mf}} = \frac{{ - \frac{{150\left( {1 - \varepsilon_{\text{mf}} } \right)}}{{\varepsilon_{\text{mf}}^{3} \Upphi_{s}^{2} }}\frac{{d_{P } \rho_{F} }}{\eta } + \sqrt {\left( {\frac{{150\left( {1 - \varepsilon_{\text{mf}} } \right)}}{{\varepsilon_{\text{mf}}^{3} \Upphi_{s}^{2} }}\frac{{d_{P} \rho_{F} }}{\eta }} \right)^{2} - 4*\frac{1.75}{{\varepsilon_{\text{mf}}^{3} \Upphi_{s} }}\left( {\frac{{d_{P} \rho_{F} }}{\eta }} \right)^{2} *\left( { - \frac{{d_{P}^{3} \rho_{g} \left( {\rho_{s} - \rho_{F} } \right) g}}{{\eta^{2} }}} \right)} }}{{\frac{3.5}{{\varepsilon_{\text{mf}}^{3} \Upphi_{s} }}\left( {\frac{{d_{P } \rho_{g} }}{\eta }} \right)^{2} }} $$
(7)
$$ u_{t} = \left( {\frac{{4 d_{p} \left( {\rho_{s} - \rho_{g} } \right)g}}{{3 \rho_{g} C_{D} }}} \right)^{0.5} $$
(8)
$$ C_{D} = \frac{24}{{\text{Re}_{p} }}\left[ {1 + \left( {8.1716e^{{ - 4.0655\Upphi_{s} }} } \right)\text{Re}_{p}^{{0.0964 + 0.5565\Upphi_{s} }} } \right] + \frac{{73.9\left( {e^{{ - 5.0748\Upphi_{s} }} } \right)\text{Re}_{p} }}{{\text{Re}_{p} + 5.378e^{{6.2122\Upphi_{s} }} }} $$
(9)
$$ u^{*} = u\left( {\frac{{\rho_{F}^{2} }}{{\eta \left( {\rho_{s} - \rho_{F} } \right)g}}} \right)^{1/3} $$
(10)
$$ d_{p}^{*} = d_{p} \left( {\frac{{\rho_{F} \left( {\rho_{S} - \rho_{F} } \right)g}}{{\eta^{2} }}} \right)^{1/3} $$
(11)

Figure 3 shows the resulting Grace diagram, including the experimental conditions for 873 K, 973 K and 1073 K reduction temperatures. As shown, the experimental conditions with constant gas flow rate are always in the area of the fluidized bed. Gas velocities below the line of minimum fluidization velocity umf will end in a fixed bed without particle movement, while gas velocities above the line of the terminal velocity ut will end in an entrainment of solid particles.

Fig. 3
figure 3

Grace diagram including experimental conditions for the reduction tests

Full size image

Results and Discussion

Experimental Results

During every experiment, the weight loss, temperature of the sample portion and pressure drop across the grid and bed were measured. Figure 4 summarizes the results for a reduction temperature of 973 K. Figure 4(a) shows the change in sample weight and the sample temperature against reduction time. It can be seen that a residence time of 4250 seconds is required to reach a constant weight signal that indicates a complete reduction. After a short increase in the sample temperature at the beginning (slightly exothermic behavior of reduction reaction from Fe2O3 to Fe3O4 at 973 K), a temperature drop of 20 K during reduction from magnetite to wüstite occurred due to the strong endothermic reaction behavior. It took some minutes to reach the required reduction temperature again, which may influence further kinetical investigations of the experiments. This happened during all experiments to the same extent due to the thermal inertia of the system. Figure 4(b) shows the measured pressure drop that occurred during the passing of the grid and sample portion (black line). The gray line only represents the differential pressure for the material without the grid. This line should be equal to the dotted black line, which represents the theoretical differential pressure drop over the material, calculated from sample mass at the beginning and the weight loss sustained during reduction. As shown, there are small deviations between these two lines. Two reasons are responsible for these deviations. One, the entrained material was not considered in the theoretical calculation. The amount of entrained material was 21.4 g during the whole reduction experiment, which represents a pressure drop of 0.6 mbar; two, there were still some inaccuracies while measuring the differential pressure across the grid under reduction conditions before the experiment itself. Figure 4(c) shows the degree of reduction and metallization against reduction time, calculated from the weight loss and chemical analysis of the iron ore shown in Table I. The progress of reduction can be divided into three stages; a fast reduction at the beginning from hematite to magnetite, followed by a nearly constant reduction rate up to 85 pc. degree of reduction. In the final stage, the reduction rate slowed down until it reached a complete reduction to metallic iron.

Fig. 4
figure 4

Experimental results for 973 K reduction temperature; (a) weight loss and temperature against time; (b) pressure drop grid and material against time; (c) degree of reduction and metallization against time

Full size image

Figure 5 shows the comparison of the reduction progress at different temperatures. All other process parameters are the same. As shown, a higher temperature increases the reduction rate, especially at the intermediate and final stages of reduction. In terms of kinetics, a higher temperature is beneficial due to the limiting effects regarding diffusion, nucleation and growth of nuclei, and chemical reaction decreases. In the case of reduction with hydrogen, a higher temperature is also preferable from a thermodynamic point of view due to the expanding stability area of iron with increasing temperatures. Figure 6 shows the comparison between experimental results and the thermodynamic equilibrium for reduction temperatures 873 and 1073 K. The thermodynamic equilibriums were calculated using FactSageTM 7.2 (Databases: FactPS, FT Oxide). Therefore, the hydrogen input flow rate and the sample amount of the experiments were used, which are similar for both experiments, given by 16.9 Nl min−1 and 400 g, respectively. Depending on the reduction temperature (for the calculation a constant reduction temperature was assumed during the whole experiment), different possible gas utilizations could be achieved, corresponding to the Baur–Glässner diagram shown in Figure 1. With the given process parameters and sample amount, the amount of oxygen which could be removed from the iron ore can be calculated and converted into a curve of reduction degree against time. That is why it takes less time for complete reduction at higher temperatures due to the expansion of Fe and FeO stability areas with increasing temperature. As exhibited, the influence regarding kinetics decreases drastically with an increasing temperature. The reduction at 1073 K proceeds near the thermodynamic equilibrium, up to 85 pc. degree of reduction. Afterwards, the reduction rate decreases. For 873 K, there is still a higher deviation between the experimental results and the thermodynamic equilibrium. Kinetic analysis should give an explanation regarding this different behavior.

Fig. 5
figure 5

Comparison of the progress of reduction at different temperatures

Full size image
Fig. 6
figure 6

Comparison of the experimental results with thermodynamic equilibrium

Full size image

Determination of Apparent Activation Energy Using the Model-Free Method

The rate constant and apparent activation energy of isothermal gas–solid reactions can be defined as follows[24]:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = k\left( T \right) \times f\left( x \right) $$
(12)
$$ g\left( x \right) = \mathop \smallint \limits_{0}^{x} \frac{{{\text{d}}x}}{f\left( x \right)} = k\left( T \right) \times t $$
(13)

where k(T) represents the temperature-dependent Arrhenius rate constant and f(x) denotes a mathematical function, which depends on the kinetic model used and remains constant at a certain temperature and gaseous concentration. Eq. [12] can be integrated to acquire the integral expression g(x). Using experimental data for conversion against time in Eq. [13], the rate-limiting step can be evaluated via the model-fitting method. The relationship among k(T), temperature T and apparent activation energy Ea is given by the Arrhenius equation, Eq. [14]. A denotes the pre-exponential factor, and R represents the gas constant. To determine the apparent activation energy, a combination of Eqs. [12] and [14] is required, which results in Eq. [15].[25]

$$ k\left( T \right) = A*e^{{ - \frac{{E_{a} }}{R*T}}} $$
(14)
$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = A*e^{{ - \frac{{E_{a} }}{R*T}}} *f\left( x \right) $$
(15)
$$ \ln \left( {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right) = - \frac{{E_{a} }}{R*T} + \ln \left( A \right) + \ln \left[ {f\left( x \right)} \right] $$
(16)

The logarithmic form of Eqs. [15] is shown in [16], to evaluate the apparent activation energy via linear regression. Figure 7 shows the reduction rates for different temperatures from 5 to 95 pc. degree of reduction, where dx/dt also represents dRD/dt. It can be seen that the reduction rate increases slightly between 30 and 50 pc. degree of reduction at high temperatures. This indicates a limitation by nucleation and growth of nuclei during the initial formation of metallic iron. For the evaluation of the apparent activation energy against the degree of reduction, the mathematical function f(x) was set to 1, which ends in a model-free fitting. The corresponding Arrhenius plot is shown in Figure 8 for different degrees of reduction. The apparent activation energies can be determined using the slope of the regression lines. As exhibited, the slope is not similar for all degrees of reduction. The resulting two-peak-shaped curve of the apparent activation energy against the degree of reduction is shown in Figure 9. The vertical lines at 11.1 and 33.3 pc. degree of reduction represent a complete reduction to Fe3O4 and FeO, respectively. The apparent activation energy rises to 55 kJ mol−1 until a degree of reduction of 12 pc. is reached, which represents nearly the complete reduction from Fe2O3 to Fe3O4. Afterwards, it decreases to 23 kJ mol−1 until a degree of reduction of 30 pc. is achieved, which indicates a nearly complete reduction to FeO. The second peak is not as drastic as the first one and goes up to 42 kJ mol−1, reaching the top at a degree of reduction of 85 pc. Two peaks can be observed during the reduction procedure, indicating that the apparent activation energy is not constant. Similar shaped curves of the apparent activation energy for the reduction of hematite fines with CO in a micro-fluidized bed reaction analyzer were determined by Chen et al.[26] A change in apparent activation energy always occurs when the change in reduction rate at different temperatures takes place in a different way. For that reason, a change in rate-limiting steps at different reduction temperatures must occur. The apparent activation energy increases with further progress of reduction from FeO to Fe, which signifies that the overall reduction may be controlled by another mechanism, e.g. chemical reaction and nucleation. It seems that the reduction from Fe2O3 → Fe3O4 has the highest apparent activation energy, followed by FeO → Fe and Fe3O4 → FeO reductions. Similar trends have been reported by Munteanu et al.[27] and Shimokawabe et al.[28]

Fig. 7
figure 7

Reduction rate against degree of reduction

Full size image
Fig. 8
figure 8

Arrhenius plot for selected conversions of experimental results

Full size image
Fig. 9
figure 9

Curve of apparent activation energy against degree of reduction

Full size image

Investigations of Kinetics

The following sections detail the kinetical investigations carried out regarding the experimental data. To achieve accurate results, conventional kinetic analysis was done using only experimental data from 33 to 100 pc. degree of reduction, so only the reduction from FeO to Fe was taken into account. For the evaluation of the total reduction processes from Fe2O3 to Fe, multistep kinetic analysis was performed.

Conventional Kinetic Analysis for the Reduction of FeO to Fe—Approach 1

To acquire knowledge regarding the rate-limiting mechanism, the model-fitting method was employed. Experimental data from 33 to 100 pc. degree of reduction, representing the reduction from FeO to Fe, was used. This assumes that the reduction to FeO was complete at 33 pc. degree of reduction. The models employed to describe gas–solid reactions are listed in Table III. They can be divided into four groups, including phase-boundary-controlled models, diffusion models, reaction-order models and nucleation models.

Table III Mathematical Models to Describe Gas–Solid Reactions[29,30]
Full size table

Figure 10 shows the fitting results of experimental data at 973 K reduction temperature using the models shown in Table III, whereby only the rate-limiting step for the reduction of FeO to Fe was determined. Plotting the integral expression g(x) against reduction time should give a straight line, with a coefficient of determination R2 close to one. The results indicate that this stage of reduction may follow the diffusion model D4, the first-order reaction model ROM1, and the nucleation model NM1 with a coefficient of determination R2 ≥ 0.98 as the three best-fitting models.

Fig. 10
figure 10

Model-fitting analysis of experimental data for reduction of FeO to Fe at 973 K using reaction models from Table III. (a) PBC and D models. (b) ROM and NM models. R2 indicates the coefficient of determination

Full size image

Table IV shows the calculated values of the coefficient of determination for each model at different reduction temperatures. The three best-fitting models are marked bold. The results show that no general trend can be observed. The diffusion model D4 fits well at all reduction temperatures, whereby at lower reduction temperature, the phase-boundary model PBC3 becomes relevant. The reaction-order model ROM1 only fits well at higher reduction temperatures, while the nucleation model NM1 fits well in a temperature range between 923 K and 973 K. In general, it is difficult to evaluate model-fitting results using only the coefficient of determination, because other models also have quite a high value of R2. Thus, it is not possible to define one rate–limiting step from the results. This type of model-fitting procedure can only give an idea about the rate-limiting step; an accurate statement is not possible.

Table IV Model-Fitting Analysis of Experimental Data for Reduction of FeO to Fe Showing Coefficient of Determination at Different Temperatures—Approach 1
Full size table

Conventional Kinetics Analysis for the Reduction of FeO to Fe—Approach 2

Another approach to defining the rate-limiting step is the fitting of selected models from Table III to experimental results by variation of the rate constant to minimize the root mean square deviation (RMSD). In this case, it can be seen in which part of the reduction the utilized model matches the experimental results. The RMSD is defined as follows[11]:

$$ {\text{RMSD}} = \sqrt {\frac{{\sum \left( {x_{\text{calc}} - x_{ \exp } } \right)}}{n - 1}} $$
(17)

RMSD was used to compare the calculation results with the experimental data, where xcalc represents the calculated values, xexp the experimental ones, and n the number of data sets. According to the results from conventional kinetic analysis Approach 1, the models PBC3, D3, ROM1, and NM1 were selected. Figure 11 shows the fitting curves of the different models for the reduction of FeO to Fe at 973 K reduction temperature; therein, x represents the experimental data. It can be seen that different models fit quite well to the experimental data at different stages of reduction, but there is still no model available that is suitable during the whole reduction process. Consequently, it seems that different rate-limiting steps act at different stages of reduction. At the beginning, the PBC3 model fits best to the experimental results, while at the final stage, the ROM1 model is the best one.

Fig. 11
figure 11

Model fitting of experimental data for reduction of FeO to Fe at 973 K via fitting rate constant of model to experimental results using selected models from Table III

Full size image

Table V summarizes the resulting values for the fitted rate constants and the corresponding RMSD at different reduction temperatures. The values for RMSD show that the models PBC3 and ROM1 fit best (highlighted in bold) at a reduction temperature ranging from 873 K to 1023 K. At 1073 K, however, the NM1 model of nucleation is the most suitable, which indicates that nucleation appears more important with increasing temperatures. This kind of analysis also assumes that the reduction to FeO is finished at 33 pc. degree of reduction.

Table V Values of Reaction Rate k and Root Mean Square Deviation RMSD Resulting from Model-Fitting—Approach 2
Full size table

Comparison of Arrhenius Activation Energy Values

Values of Arrhenius activation energy are defined for the best-fitting models from Approach 1, as well as for all models used from Approach 2. From the first approach, k values were determined from the slopes of the regression lines corresponding to Figure 10. For the second approach, k values were provided by the fitting procedure. The resulting Arrhenius plots for both approaches are given in Figure 12. As shown, all regression lines show good coefficients of determination close to 1.

Fig. 12
figure 12

Determination of apparent activation energy from different model analyses for the reduction from FeO to Fe; (a) Approach 1; (b) Approach 2

Full size image

Table VI shows the resulting values of apparent activation energy, determined by the slope of the regression lines. The apparent activation energy for the reduction of FeO to Fe by hydrogen is in the range of 29 to 35 kJ mol−1 for every model used. Summarized values of apparent activation energy for the reduction of FeO to Fe, reported in the literature, are given in Table VII. The values vary in a range between 11 and 104 kJ mol−1. Notably, the apparent activation energy depends on many parameters, such as input material, gas composition, type of experiment, etc.[18] Moreover, the occurring rate-limiting step is of importance. For example, Kuila et al.[31] defined diffusion as a rate-limiting step, so the apparent activation energy determined is only 11 kJ mol−1.

Table VI Determined Values of Apparent Activation Energy from Different Model-Fitting Analyses
Full size table
Table VII Values of Apparent Activation Energy for the Reduction of FeO to Fe, as Reported in Literature
Full size table

For the first two fitting approaches, using integral expression g(x) and the coefficient of determination as well as model-fitting via variation of the rate constant k, no general trend can be assumed using only experimental data for the reduction of FeO to Fe. The use of the g(x) function for model-fitting shows that diffusion also might be a limitation for the reduction process, which is untypical for the reduction of hematite with hydrogen due to the good diffusion behavior of hydrogen compared to carbon monoxide.[36] If dense iron layers formed during reduction do not occur, limitation by diffusion should not be of importance during reduction. To evaluate this, polished micro-sections of partly reduced samples with approximately 40, 60, and 80 pc. degree of reduction are shown in Figure 13. It can be seen that the metallic iron formation starts uniformly and is then distributed in the whole particle area, not only on the outer surface of the particle. For that reason, a growing layer of metallic iron around the particle does not occur. This finding confirms that diffusion of the reducing gas to the reaction interface is not significant, especially at the beginning of the metallic iron formation. It seems that only nucleation and chemical reaction may limit the progress of reduction in this case. Further multistep kinetic analysis should confirm this theory.

Fig. 13
figure 13

Polished micro-sections to evaluate progress of reduction: (a) 40 pc. degree of reduction; (b) 60 pc. degree of reduction; (c) 80 pc. degree of reduction; FeO, gray areas; Fe, white areas

Full size image

Multistep Kinetic Analysis of Total Reduction from Fe2O3 to Fe Using a Parallel Reaction Model Based on the JMA Model

A classic model to describe isothermal gas–solid reactions is the model defined by Johnson–Mehl–Avrami (JMA),[37,38,39,40] as shown in Eq. [18],

$$ x = 1 - e^{{ - a*t^{n} }} $$
(18)

where x represents the conversion, a the nucleation rate constant, t the reduction time and n the kinetic exponent. If n  < 1, the mechanism is considered to be diffusion controlled; if n is close to 1, the reaction is controlled by reaction kinetics. A value of n  > 1.5 shows that the reaction can be explained by the nucleation process, where n =1.5 represents a zero nucleation rate, n =1.5 to 2.5 a decreasing nucleation rate, n =2.5 a constant nucleation rate and n  > 2.5 an increasing nucleation rate.[41] The rate constant k can be determined according to Eq. [19].

$$ k = a^{{\frac{1}{n}}} $$
(19)

To evaluate more than one process occurring in parallel, a combination of three mechanisms was chosen to reproduce the experimental results as accurately as possible, as shown in Eq. [20], where x0 represents the conversion at the beginning of the analysis and w1,2,3 the weight factors for three different limiting process steps.

$$ x_{t} = x_{0} + w_{1} x_{1} + w_{2} x_{2} + w_{3} x_{3} $$
(20)

A combination of Eqs. [18] and [20] leads to Eq. [21], considering that x0 is zero at the beginning of the analysis.

$$ x_{t} = w_{1} *\left( {1 - e^{{ - a_{1} *t^{{n_{1} }} }} } \right) + w_{2} *\left( {1 - e^{{ - a_{2} *t^{{n_{2} }} }} } \right) + w_{3} *\left( {1 - e^{{ - a_{3} *t^{{n_{3} }} }} } \right) $$
(21)

A similar procedure was carried out by Monazam et al. for the investigation of the oxidation from Fe3O4 to Fe2O3,[42] as well as for the reduction of hematite by methane.[43] Fitting Eq. [21] to experimental results was performed using the solver function of Microsoft Excel by a variation of w1,2,3, a1,2,3, and n1,2,3, to minimize RMSD from the fitting and experimental results. The results of the fitting procedure are exhibited in Figure 14 for different reduction temperatures.

Fig.14
figure 14

Kinetical investigation based on JMA model (parallel) at temperatures (a) 873 K, (b) 923 K, (c) 973 K, (d) 1023 K, (e) 1073 K

Full size image

It can be seen that the initial stage of reduction might be controlled by chemical reaction in a temperature range from 873 K to 973 K, indicated by a kinetic exponent n1 close to one. The corresponding weight factor is in the range for a complete reduction of Fe2O3 to Fe3O4. At higher reduction temperatures, the kinetic exponent n1 decreases below 1 with a simultaneous increase in the weight factor. This means that at higher temperatures, the initial stage of reduction might be controlled by diffusion, whereby it cannot be distinguished between reduction of Fe2O3 to Fe3O4 and that of Fe3O4 to FeO. Accordingly, at higher temperatures, it seems that both reduction steps occur in parallel and are not clearly separated from each other. The modeling results of further reduction show that the process is controlled by a mixture of first-order kinetics and nucleation. At low temperatures, first-order kinetics are dominant. An increasing temperature leads to a decrease in weight factors, with a nearly constant kinetic exponent n2 around 1.25. The influence of nucleation becomes more evident with increasing temperatures. At 1073 K reduction temperature, only nucleation is important. The influence of nucleation can also be seen in the shape of the reduction rate in Figure 7. At the end of the reduction to FeO, the reduction rate is lower compared to the later stages, e.g. 40 pc. degree of reduction. This represents an incubation time for the nucleation of metallic iron. At the end of reduction, nucleation is no longer important, and the reduction rate is only controlled by the chemical reaction. Due to the good diffusion behavior of hydrogen, diffusion does not limit the reduction rate in the final stages of reduction. Table VIII summarizes the resulting values of weight factors, nucleation rate constants and kinetic exponents at different reduction temperatures.

Table VIII Weight Factors, Nucleation Rate Constants, Kinetic Exponents, and RMSD for Multistep Kinetic Analysis (Parallel) at Different Temperatures
Full size table

To evaluate which mechanism is acting at a certain degree of reduction, Figure 15 shows the different mechanisms plotted against the experimental degree of reduction: (a) w1, (b) w2, and (c) w3. It is clearly visible that in early stages of reduction, the controlling mechanism changes with increasing temperatures from first-order kinetic to diffusion with increasing weight factor. This results in higher reduction rates at higher temperatures for higher degrees of reduction (20 to 30 pc.). This outcome corresponds to the first peak of the apparent activation energy at a degree of reduction of 12 pc. Furthermore, the weight factor of nucleation increases with increasing temperatures; simultaneously, the weight factor of first-order kinetic decreases. Different changes occur in the reduction rate at certain degrees of reduction, which matches to the second peak of the apparent activation energy at a degree of reduction of 85 pc. Afterwards, only the first-order reaction is significant, which is why the apparent activation energy decreases. These findings are in agreement with those of the polished micro-sections, displayed in Figure 13. For the reaction mechanisms two and three, representing first-order kinetics and nucleation, activation energies of 19.30 and 33.88 kJ mol−1 can be determined, respectively. These values are in good agreement with those shown in Figure 9, where the activation energy increases from 23 to 42 kJ mol−1, where both mechanisms are acting in parallel. In the final stage of reduction (RD > 90 pc.), nucleation is not important anymore. The activation energy decreases to the value representing only limitation due to first-order kinetics.

Fig.15
figure 15

Plot of different weight factors (w) for different temperatures against degree of reduction: (a) w1; (b) w2; (c) w3

Full size image

Conclusions

A laboratory fluidized bed reactor was used to investigate the reduction kinetics of a fine hematite ore to metallic iron by hydrogen at temperatures from 873 K to 1073 K. Different approaches for kinetic analysis were used to evaluate the rate-limiting step. Several conclusions can be drawn. First, the influence of kinetic limitation on the reaction rate of reduction reactions decreases drastically with increasing temperatures. At 1073 K, the reduction proceeds near the thermodynamic equilibrium, while at 873 K, the deviation between experimental results and thermodynamic equilibrium is much higher. Second, the reaction kinetics of hematite reduction by hydrogen cannot be described using only one simple gas–solid reaction model. The limiting mechanism varies with temperature and the degree of reduction. Therefore, the apparent activation energy is not constant during the reduction procedure. Third, a two-peak-shaped curve of apparent activation energy against degree of reduction was determined, whereby the apparent activation energy varies from 11 to 55, 55 to 23, and 23 to 42 kJ mol−1 for the reduction of Fe2O3 to Fe3O4, Fe3O4 to FeO, and FeO to Fe, respectively. Fourth, polished micro-sections show that at the beginning of metallic iron formation, the iron is formed uniformly and distributed in the whole particle, which indicates that diffusion of the reducing gas does not limit the reduction in this case. Lastly, multistep kinetic analysis using the JMA model shows that the initial stage of reduction might be controlled by first-order kinetics and diffusion, depending on the temperature. The reduction of FeO to Fe is limited by first-order kinetics and nucleation, whereby the importance of nucleation increases with rising temperatures. Moreover, diffusion is not important in the case of fluidized bed reduction, using hydrogen as a reducing agent during the reduction from FeO to Fe.