Abstract
An experimental heat treatment chamber and control system were developed to perform in-situ X-ray diffraction experiments during low-pressure carburizing (LPC) processes. Results from the experimental chamber and industrial furnace were compared, and it was proven that the built system is reliable for LPC experiments. In-situ X-ray diffraction investigations during LPC treatment were conducted at the German Electron Synchrotron Facility in Hamburg Germany. During the boost steps, carbon accumulation and carbide formation was observed at the surface. These accumulation and carbide formation decelerated the further carbon diffusion from atmosphere to the sample. In the early minutes of the diffusion steps, it is observed that cementite content continue to increase although there is no presence of gas. This effect is attributed to the high carbon accumulation at the surface during boost steps which acts as a carbon supply. During quenching, martensite at higher temperature had a lower c/a ratio than later formed ones. This difference is credited to the early transformation of austenite regions having lower carbon content. Also, it was noticed that the final carbon content dissolved in martensite reduced compared to carbon in austenite before quenching. This reduction was attributed to the auto-tempering effect.
Similar content being viewed by others
1 Introduction
The case hardening by carburizing and subsequent quenching processes is currently a widely used surface hardening treatment.[1] By carburizing, a high-strength surface layer and a tough core is set, which in particular has a positive effect on the wear and fatigue properties of the component.[2] Moreover, compressive residual stresses are generated in the case, which also contributes to an improvement of the fatigue strength. Among other carburizing techniques, low-pressure carburizing (LPC) has an increasing practical importance in today’s industrial manufacturing since it leads to high carbon activity which enables wide surfaces and also blind holes to be uniformly carburized.[3] Compared to standard gas carburizing, during LPC the carbon donor is oxygen free. This avoids any detrimental surface oxidization.
Because of the utilization of an oxygen free atmosphere composed from hydro carbons, no equilibrium reactions are involved in the carburizing reaction. Thus, the carburization cannot be automatically controlled based on the common approach in gas carburization using an oxygen probe or gas-analyzers. LPC is, therefore, a recipe-controlled thermochemical treatment that is generally composed of several boost and diffusion steps. Before the carburizing process, samples are typically heated to around 800 °C in a nitrogen atmosphere and then heated to final carburizing temperature under vacuum, which is typically in the range of 920 °C to 960 °C. Typical pressure of the atmosphere in vacuum-phase is about 5 × 10−2 mbar. Subsequently, carbon donor gas is introduced into the furnace at low pressure (1 to 30 mbar). During this step, dissociation and adsorption of the acetylene molecules on the surface and subsequently the absorption of carbon atoms into the steel take place leading to an increasing carbon content in the case of the workpiece.[4] This enrichment of surface by carbon is often called boost step. Afterward, the furnace is evacuated from the remaining gases to let the carbon diffuses toward the core of the workpiece. Thus, the carbon content close to the surface decreases and a carbon profile with increasing depth results, so that in the next boost step the material can absorb further carbon. This step is often called diffusion step. This sequence of boost and diffusion steps can be repeated several times until the desired carbon profile is achieved. The process-related parameters such as temperature, number and duration of boost/diffusion steps, carburizing gas flow rate and pressure can be varied to achieve the desired case profile. Different types of process strategies can be found in industrial applications.[5] When the desired carbon profile is reached, samples are generally quenched, i.e., with high-pressure inert gas such as helium or nitrogen, or in oil to get the desired martensitic microstructure with a hardness gradient toward the core. Several hydrocarbon gases can be used as carbon donor gas such as propane, ethylene or acetylene. However, LPC using acetylene is particularly economical and environmentally friendly[6,7]; also more effective since acetylene directly participates the carburizing reactions rather than pyrolyzing other carburizing gases.[8] Although the LPC is established in industry, it still lacks some detailed mechanisms of microstructural evolution and basic understanding. Especially, local carbon enrichment, which leads to successive carbide formation and dissolution during different process steps, is still missing. This lack of information exhibits the necessity of a better understanding of the process.
Currently, there are several good approaches for optimization of process parameters and understanding of the process,[8,9,10,11,12] but common methods are often limited to the characterization of initial and final stages or interruption of the process by cooling. This especially causes a change in the properties of materials because of the multiple transformations occurring and a loss of information. For this reason, it is of great interest to find a description of the carburizing kinetics and description of solid solution development as well as phase composition of the case that applies generally to all stages of the process. This investigation is only possible by getting real-time insights into the process and material transformations during LPC combined with a spatially resolved analysis. In-situ X-ray diffraction methods, in particularly synchrotron X-ray diffraction approaches, are excellently suitable for obtaining information about microstructural evolution[13,14,15] and redistribution of interstitials.[16] Moreover, structure evolutions during other thermochemical surface treatments such as nitriding could also be observed successfully by in-situ synchrotron diffraction techniques.[17] An investigation regarding LPC in this aspect, as far as the authors know, was never done previously. Therefore, the primary goal of this study is to validate the employed methodology, and extend the current state of knowledge and understanding of LPC on the base of in-situ X-ray diffraction experiments. In this manner, time-resolved qualitative and quantitative information related to microstructures, present phases and interstitials can be gathered during the entire process.
This paper describes the developed heat treatment chamber and the related control system designed for in-situ X-ray diffraction analyses in both transmission and reflection mode. Moreover, it gives some initial results about development of solid solution of carbon, microstructural evolution, carbide formation and carbon diffusion during LPC process. For this, in-situ synchrotron X-ray diffraction experiments in transmission mode were performed during complete LPC including subsequent quenching at the Deutsches Elektronen-Synchrotron (DESY) in Hamburg, Germany. The microstructural evolution was evaluated with high spatial and time resolution, while additional metallographic investigations were performed after the process to confirm the observations made at high temperature during process.
2 Material and Experimental Procedure
2.1 Material and Sample Preparation
The in-situ diffraction analyses were performed using samples made of case hardening steel AISI 5120 (EN 20MnCr5). Chemical composition of the steel is given in Table I.
Samples were machined to rectangular prism shape with dimensions of 5 × 14 × 14 mm3. To eliminate carbon diffusion from undesired sides, five surfaces, except the surface that is aimed to be carburized, of the samples were coated with a 5-8 µm thick Zirconium nitride (ZrN) layer by using the PVD method. The effectiveness of the coating was proved by comparing the carbon diffusion depth profiles of coated and uncoated samples after carburization in an industrial furnace according to the parameters given in Figure 2. Depth profile measurements of the elemental distributions were done with GD-OES (glow discharge optical emission spectrometry) and S-OES (spark optical emission spectroscopy). According to the measurement results given in Figure 1, increased carbon content is present in the first 5 µm but after that carbon content rapidly reduces to about 0.3 pct and then reaches the base carbon content at a depth of approx. 180 µm; on the other hand, the carbon content of the uncoated sample increased from about 0.2 pct up to about 0.8 pct. Therefore, diffusion of carbon from side surfaces was mostly suppressed with ZrN coating. Since XRD measurements in transmission will give an integrated signal coming from the whole thickness of 5 mm (see Figure 2(b)), the increased carbon content within the first 5 µm represent roughly 0.1 pct of the total signal which appears neglectable.
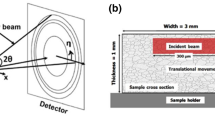
Experimental set-up for the in-situ XRD measurement during LPC: Process scheme (a); alignment of sample and heaters (b); picture of chamber and 2D detector (c); picture of chamber (d). Number 1, 2, 3, 4 and 5 are beam in window, beam out window, gas inlet pipe, vacuum outlet pipe and heated sample respectively
2.2 Chamber Design and Process Parameters
To produce a process chamber, the cylindrical body and the top cover were cut from a stainless steel tube and welded together. Two circular windows were machined to allow the beam path for transmission measurement. Two extra longitudinal windows on the left and right sides for reflection measurement were also machined on the chamber body. Standard ISO-KF flanges were welded to the circular windows to form a viewport shape. These ISO-KF flanges and two longitudinal window openings were then covered with Kapton foils with 75 µm thickness to allow easy penetration of the X-ray beam.
Acetylene (C2H2) was used as carbon donor gas and helium (He) was used as quench gas. Gas supplies of the process were adjusted with two mass flow controllers, which are controlled by a Protherm 510 process control unit from United Process Controls GmbH/Germany. The pressure was measured by using a capacitance manometer and regulated by a remote-controlled electromagnetic valve. To avoid any damage caused by high helium pressure during quenching in the case of failure of a vacuum pump or electromagnetic valve, a safety valve adjusted to an open pressure of 33 mbar was connected to the chamber.
The sample was heated up using SiN ceramic heating elements connected to an external power supply. The voltage of the power supply was also adjusted by the process control unit. The temperature was measured using K-type mantle thermocouple inserted into a hole at the side of the sample and data were recorded by using a Eurotherm temperature controller from Schneider Electric Systems Germany GmbH, Germany. All electrical components inside the chamber were made of copper-free material to eliminate any risk of acetylide formation since acetylides are sensitive to temperature, friction and bear a risk of explosion.[18]
Process scheme and experimental set-up are presented in Figure 2. The heaters were placed in such a manner that a region in the center of the sample was accessible for the measurements with scanning over the z-axis (see Figure 2(b)). The gas inlet pipe was placed at the top and the vacuum outlet pipe was placed at the bottom of the cylindrical chamber ensuring that sample stayed in the middle of the gas flow. One extra type-K thermocouple was also attached outside of the chamber to measure the chamber temperature. At the beginning of each process, the sample was placed between four SiN ceramic heating elements (see Figure 2(b)) and the chamber was evacuated until the pressure of 10−1 mbar was reached. The sample was then heated up to the process temperature of 940 °C with an average heating rate of 2 K/s in order to achieve a full austenitic state. Such high temperatures are necessary for maintaining higher solubility in austenite and an increased diffusion rate. When the process temperature was reached, the first boost step was started by introducing acetylene into the chamber with 1.2 bar pressure and a rate of 10 mL/min (8.4 m3/m2h) for 1 minute. In the presence of acetylene, the pressure inside the chamber increased up to 4 mbar. After the end of the first boost step, remaining gases were evacuated from the furnace and the temperature was kept on 940 °C for 20 minutes to enable carbon diffusing in the sample to expand the carburizing region. This was the end of one boost and diffusion cycle (see Figure 2(a)). This cycle was repeated two times more with varying boost and diffusion durations to reach the desired carbon profile. After the repetition of cycles, the temperature was slowly decreased to 840 °C within 10 minutes and kept constant at this temperature for further 15 minutes for temperature homogenization, further diffusion and to ensure a low carbon content in solution in the austenite. This temperature decrease is necessary to reduce distortion due to severe thermal gradients. When this step is done, the sample is quenched down to less than 100 °C using helium gas at 5 bar. The entire duration of this final step was about 90 seconds.
Different experiments with various process parameters were conducted and each experiment was repeated at least once to prove the consistency of the newly developed system. This paper focuses on one set of process parameters since they are based on an industrially proved simulation result to reach approximately 0.8 pct surface carbon content and a targeted case hardening depth (CHD) of about 0.6 mm which is a common case profile in industry. In the following chapters, the results of two different samples (sample 1 and 2) carburized using the above-mentioned parameters will be presented and discussed. The first sample will be in the main focus but the results of the second sample are given to support the outcomes.
2.3 X-ray Diffraction Measurements
The diffraction experiments were performed at beamline P07-EH3 of the PETRA III Synchrotron at DESY/Hamburg with a high energy monochromatic X-ray beam (103.4 keV) which permits to work in transmission through the whole 5 mm thickness of the steel sample. The primary beam height was adjusted to 20 µm to achieve a satisfying spatial resolution in the direction of the carbon gradient, while the beam width was chosen as 1000 µm to obtain good statistical conditions in terms of diffracting domains.
Fundamental phenomena that should be clarified were the microstructural evolution and carbide formation/dissolution taking place at the very surface region of the sample. Therefore, for the samples examined in this paper, the position of the beam was always kept constant directly at the surface with an acquisition time of 0.2-0.5 s/frame during the boost steps. The determination of the surface position was achieved by surface entry scans, which were repeated several times during the whole process to adjust the beam position if required. During diffusion, hardening and quench steps, the sample was either kept constant for beam to focus directly on the surface with acquisition time of 0.5-1 s/frame, or continuously moved along z-axis to scan over the depth from the carburized surface. Continuous scanning of the sample was made with 24 steps with accusation time of approx. 3.75 seconds up to approx. 500 µm depth. With this strategy, microstructural evolution, carbide formations and carbon diffusion could be successfully observed by using a 2D detector (Perkin-Elmer with 2048 × 2048 px and a pixel size of 200 µm) placed 1.325 m behind the sample. Full diffraction rings were measured in the 2θ-range of 0 to 12 deg with a time resolution of 0.2-0.5 seconds. Temperature information was received through a thermocouple with a time resolution of 1 s/data. Special attention was paid to combine the temperature and diffraction data having different time resolution to assure a perfect continuity in between different steps without any artifacts.
The 2D patterns were full 360° azimuthally integrated by using the fast PyFAI software of ESRF.[19] For a detailed analysis of the evolution of lattice parameter and phase fractions, the integrated diffraction patterns were analyzed using the convolution-based Rietveld refinement implemented in TOPAS 6.0 Academics (Coelho Software, Australia).[20] This way, the observed diffraction peaks are modeled by convolution of various functions that represent the instrumental and sample contributions to the peak profiles.[21] The instrumental contributions to the diffraction peak profiles were determined using measurements of a 5 mm thick (same as sample thickness) standard LaB6 NIST SRM660C powder sample. Determined fitting parameters were then fixed and used as instrumental function of the data analysis. Low background was achieved by systematic and automatic dark-image correction of the detector and therefore, only polynomial fitting of the low background was necessary in the refinements. For first approximation, during boost, diffusion and hardening steps, only austenite and cementite (Fe,Cr)3C were taken into account. For the quenching step, the microstructural model containing austenite and martensite with a tetragonal lattice was used.
2.4 Post-Process Examination
At the end of the treatment, metallographic analysis was performed on the sample to determine the present microstructure and phases. After this examination, electron micro probe analysis (EMPA) was employed to verify the elemental distribution and micro-hardness measurement were carried out to determine the hardness distribution from the surface to the core. For metallographic investigation, cross-section of the samples were ground, mechanically polished, and subsequently etched with 3 vol. pct nital solution for 30 seconds. EMPA measurement were performed using a Jeol JXA-8200 device. The measurements were done from the surface to depth of 1 mm covering a width of 100 µm. Increment size was 1 µm in each direction with 20 ms/increment measuring time. Micro-hardness measurement were carried out by using a Leco-Universal LM series micro-Vickers hardness tester. Different forces from 5 to 300 N were maintained for 15 seconds of dwell time and then an average value of the hardness was obtained. The case hardening depth (CHD) was determined as the distance from the surface where the hardness is 550 HV.
3 Results
As stated before, two samples (sample 1 and sample 2) were carburized with parameters mentioned in the previous section. Figure 3 gives a sequence of integrated diffraction patterns of sample 1 recorded at a fixed position directly below the carburized surface of the sample.
Top: Integrated diffraction patterns of sample 1 during the whole process: (he) heating, (b1) boost 1, (d1) diffusion 1, (b2) boost 2, (d2) diffusion 2, (b3) boost 3, (d3) diffusion 3, (ha) hardening and (q) quenching steps. Bottom: Shift of the γ{111} austenite peak in different boost steps. The blue arrow shows the direction of the shift
During the heating step (he), phase transformation can be identified by the disappearance of α{110}, α{200} and α{211} peaks, and appearance of γ{111}, γ{200}, γ{220} and γ{311} austenite peaks. When the first boost step starts (b1), the austenite peak shift to lower 2θ angles can be clearly observed. After the acetylene interacted with the hot surface of the sample, peak shifting was very fast in the first couple of seconds. In the following, the peak positions stay almost constant although there was a persistent presence of acetylene. In the following 20 minutes diffusion step (d1), a slow shift of the austenite peaks back to higher angles can be systematically observed.
During the second boost step (b2), the austenite peaks again shift further to lower 2θ angles. Similar to the first boost step (b1), the degree of shifting is very high within the first seconds of acetylene introduction. In consequence, the peak positions stay almost constant until the end of total two minutes duration. In the following diffusion step (d2), the austenite peaks again shift back to the higher 2θ angles very slowly.
During the final boost step, similar peak shift to lower 2θ angle can be observed; but unlike other boost steps, after a very sharp initial shift, peak positions continue to shift lower 2θ angle instead of staying constant. In following diffusion step, similarly to the other two, peaks shift back to higher 2θ angle very slowly.
After three boost and diffusion cycles, the temperature was reduced to 840 °C for the hardening step (ha). In this step, the intensity of the peaks reduced because of thermal shrinkage of the sample. During the process, an increase or a decrease in the sample volume took place due to process-related temperature changes. These changes caused the sample surface to drift from the pre-defined beam position so intensity reduced. When this happened overly, the sample position was adjusted to suitable values until good intensity was attained. In the last steps of the process, the sample was quenched with high-pressure helium (q). Strong peak shifting toward higher 2θ angle can be observed in the first seconds and in the further course the peaks continue to shift slowly. The martensitic transformation can also be observed in this step with the appearance of α′{110}/{011}, α′{200}/{002} and α′{211}/{112} martensite peaks displayed with red arrows in the quench step. Also, austenite peaks are still present after quenching, indicating the presence of retained austenite.
In the industrial furnace, carburizing and gas quenching are carried out in separate chambers. Moreover, in the industrial process all volume of the furnace, rather than only the sample, is heated and this makes temperature control easier compared to the experimental chamber. Furthermore, the absence of measurement windows makes the sealing of the industrial furnace better in contrast to the experimental chamber. Lowest vacuum reached in the experimental chamber was about 10−1 mbar while using an industrial furnace a vacuum of 5 × 10−2 mbar could be reached. Existence of these process and equipment related differences necessitate the proof of the accuracy of the experimental chamber. Therefore, a complementary LPC treatment with parameters given in Figure 2 was conducted using an industrial furnace. By this means, phase contents, carbon contents and micro-hardness values of sample 1 and the sample from the industrial furnace were compared. Results of metallographic analyses of the two samples are given in Figure 4.
Overview pictures of the cross-section show a similar transition point for both sample at a depth of approx. 550 µm depth from high carbon to low carbon microstructure. At the surfaces, mainly martensitic structure with a similar amount of retained austenite is observed in both samples. In addition MnS inclusions from the base material can be seen for both samples. Slight color difference between the core microstructures can also be distinguished which are attributed to slight differences in etching time.
Figure 5 shows carbon content and micro-hardness depth profiles for three samples carburized using the same parameters. Spark optical emission spectroscopy (S-OES) was used to determine the carbon profiles of the samples from the industrial furnace. Since the carburized surface of the sample from the experimental chamber was too small for S-OES, electron microprobe analyses (EMPA) was used to measure the carbon profile of this sample.
Carbon contents of all three samples are close to each other, but samples carburized in the industrial furnace have slightly higher carbon contents especially within the first 200 µm. Since the samples were measured by different methods, it is difficult to make a final judgment for these small differences. Moreover, the overall hardness distribution of the samples is quite similar and the case hardening depth (CHD) of the samples processed by using the experimental chamber, batch 1 and batch 2 are 0.62, 0.64 and 0.66 respectively. Therefore, the effect of lower carbon content was not confirmed by means of the hardness distribution.
Considering the results of the post-process characterization in comparison with an industrial process condition, it can be said that results obtained from two different systems are very close to each other and the newly developed process chamber is suitable to make LPC experiments with very good results comparable to an industrial process.
4 Extended Analysis of In-Situ Data and Discussion
Peak shift toward lower and higher 2θ angles respectively during boost and diffusion steps, where the temperature was kept almost constant, is an indication of a lattice parameter change. After analyzing the integrated diffraction patterns, the austenite lattice parameter change of sample 1 from the beginning of the first boost step to the end of the process was acquired for measurements performed in the materials volume close to the very sample surface and presented in Figure 6.
A cyclic change of the lattice parameter during boost and diffusion steps can be observed. The evolution of the lattice parameter can be accounted for three contributions: the chemical effect (changes in solid solution), the thermal effect and the stress induced effect. During the boost and diffusion steps the temperature is mostly stable (within few °C), the sample is austenitic and homogeneous in terms of composition. Because of the present temperature, the effective stress relief and transformation from ferrite to austenite will relax all residual stresses that existed previously in the sample so it can be considered as stress-free. Therefore, the increase and decrease of the lattice parameter can only be attributed to change of carbon content in solid solution in the austenite. In the quenching step, a very sharp decrease in lattice parameter occurs due to thermal contraction. In the following sections, the boost steps, the diffusion and hardening steps and the quenching step are analyzed and discussed separately in order to reveal the inherent mechanisms.
4.1 Boost Steps
The prediction of carbon content can be done from the dilation of the austenite crystal lattice, i.e., by the change of the austenite lattice parameter due to the occupation of octahedral sites of the austenitic lattice by carbon atoms. For this, the model developed by Onink from neutron diffraction experiments taking into account the thermal effect was applied.[22] According to the model the austenite lattice parameter is formulated as;
where \( x_{\text{C}}^{\text{r}} \) is at. pct carbon and T is the temperature in K. Using this approach the carbon content was calculated for the boost steps. Figure 7 shows the change of average carbon content dissolved in austenite during the boost steps for two different samples after conversion into mass pct.
Calculated change of average carbon content dissolved in austenite in the measured surface area of sample 1 (a) and sample 2 (b) for three different boost steps. The measured region is averaging from the surface to a maximum of 20 µm below the sample surface (according to the beam height). Error bars are shorter than symbols
All boost steps of the two samples show a very similar tendency so it can be concluded that the experiments had a good consistency and that the observed effects are significant and reproducible. During the first boost step, the carbon increase is very steep at the beginning and then stays almost constant for both samples. The average carbon content of sample 1 increased from 0.2 up to about 0.92 pct in the first 20 seconds and then continued to increase very slowly to approx. 0.94 pct until the end. Similar to sample 1, the average carbon content of sample 2 also increased up to about 0.87 pct in 20 seconds and then slowly increased further up to approx. 0.91 pct until the end. Although acetylene was continuously introduced with the same rate into the chamber, a more or less constant carbon content can be observed in the measured volume of two samples after 20 seconds so apparently a steady state seems to be reached. These values are lower than the solubility limit of austenite at 940 °C. This is because measurements were made from surface to 20 µm depth (beam height) so carbon content is the average value from probed area, where saturation is not reached everywhere in particular in boost 1.
The reason for the mostly constant carbon content within this probed volume is that acetylene decomposes to atomic carbon and gaseous hydrogen immediately when it comes in contact with the thermally activated metal surface under low pressure.[23] The limit for carbon transfer is the acetylene adsorption rate at the surface (free reaction sites for adsorption) and diffusion rate of carbon from surface into the bulk in austenite.[4] Free carbon diffuses therefore directly into the sample at a very high mass transfer rate in early seconds of the boost step and accumulates in the austenite grains at the surface. When the maximum solubility is reached, a very fine cementite (\( {\text{Fe}}_{3} {\text{C}} \)) layer is formed in the first few microns of the surface. Other hydrocarbons such as propane or methane are thermally decomposable so they break down to their components under heat. Acetylene, however, is a catalytically decomposable hydrocarbon so it requires heat and also a metal catalyzer for decomposition.[5,24,25] Therefore, it is also expected that this carbide layer influences the acetylene decay negatively by blocking the reaction sides, and autocatalytic acetylene decomposition reaction is inhibited.[26,27,28,29,30] Although the carbon diffusion still continues in the material, carbon accumulation at the surface and carbide layer formation decelerate carbon transfer from atmosphere to material. Diffusion in the material continues through the all sample, but in the present case the probed region is from surface to maximum 20 µm. Therefore, after 20 seconds, carbon increasing effects are either dissolution of cementite or limited amount of carbon diffusion through cementite; on the other hand carbon decreasing effect is the diffusion of carbon through the core. Since the probed area is highly dominated by carbon accumulation, this conceals the observation of these increasing and decreasing effects.
As a conclusion, the observed steady-state condition can be attributed to the effect of carbon accumulation at the surface leading to the formation of cementite layer, which slows down further carbon absorption of the sample from atmosphere. Thus, carbon content change is mostly governed by material dominated diffusion reactions which are rather slow.
The addressed carbide formation was confirmed by the in-situ diffraction experiment. As an example for sample 1 growing cementite diffraction peaks during the boost steps can be observed in Figure 8.
During the first 10 seconds of the first boost step, no indication of carbide peaks can be observed since the saturation limit was not reached yet. In consequence, the amount of carbon dissolved in austenite was still continuously increasing. It is worth to point out that the time required for signals, valve openings, gas transportation and acetylene decomposition reaction are also included in these 10 seconds so actually austenite saturation was reached less than 10 seconds from the start of the first carbon absorption in austenite. After the saturation limit was reached, carbides started to form so small carbide peaks can be identified near the {111} austenite peak in the diffraction pattern starting from 12 seconds of boost time. Saturation of the austenite at the surface was assumedly only 2-3 µm from the top because the average carbon content at the measured height stayed constant at 0.94 pct. This is an indication that there is a significant carbon gradient between the very top surface and a depth of about 15-20 µm below the surface. If it is assumed that the carbon content at the very top surface has to be about 1.35 pct, which is the maximum solubility limit in austenite at process temperature, there must be a very low carbon content in the remaining measured region (total measured height is 20 µm beam height) that an average value of about 0.94 pct can be determined by means of the in-situ diffraction experiment.
Carbides started to dissolve slowly in the following diffusion step. After approximately 2 minutes of diffusion, carbides were almost completely dissolved. As a consequence the carbide peaks disappear. According to the measured data the carbides have fully dissolved during the diffusion phase so that no alloy element aggregation in carbides were realized. Otherwise a full dissolution of carbides could not have happened during diffusion phase because manganese or chromium stabilize carbides and increases the dissolution temperature of carbides significantly (above 1000 °C).[31]
The carbon content in the second boost step showed similar behavior as in the first boost step. However, for this step, the determined average carbon content dissolved in austenite reaches 1.28 pct for sample 1 and 1.23 pct for sample 2, which is close to the approximate solubility limit of austenite (1.30 pct) determined with thermocalc software for the defined steel at 940 °C. Since the carbon absorbed from the first cycle was already existent, the average carbon content in this step was higher than in the first boost step. However, it is still lower than the maximum solubility limit of austenite, which is again an indication that there is still a carbon gradient within the probed sample volume. The carbide formation kinetics of sample 1 in the second boost step was also similar to the first boost step. After the saturation limit of austenite was reached, carbides started to form and remained present until the end of the boost step. In the subsequent diffusion step, carbides started to dissolve slowly.
In the third boost step, similar phenomena in regard to the carbon content can also be observed. Saturation of austenite in the surface was reached in about 8 seconds for both samples, which is faster than in case of the first two boost steps. This is attributed to the high initial amount of carbon dissolved in austenite leading to a fast saturation. However, after the saturation limit is reached and cementite precipitations are observed at the surface, the carbon content does not stayed constant like observed for the first two boost steps, but rather continues to increase. The reason of this difference in the kinetics can be the distribution of carbides in the surface layer. Formation and re-dissolution kinetics of carbides highly depend on a variety of parameters such as their size,[32,33] on the base carbon content, favorable formation sites and on the alloying elements.[4] Moreover, if the carbides are formed locally without covering the entire carburizing surface, their effect on carbon diffusion rates may vary. Thus, carbon absorption may still continue in the presence of carbides. Hence, if the surface manages to stay active for acetylene decomposition, it might be possible that carbon atoms can still diffuse through the cementite layer. In these cases, carbon absorption from the atmosphere does not stop completely but slows down, since cementite has a lower diffusion coefficient for carbon than austenite as already given previously.[34,35] Figure 8(c) shows carbide peaks of sample 1 for the third boost step. Carbide formation again started to form immediately after saturation of austenite and their amount increased until the end of the step. During following diffusion, they dissolved slowly.
To determine the carbide formation sites and the thickness of the carbide layer at the surface, one sample was directly quenched after boost step to suppress any potential carbide dissolution. After quenching, sample was scanned with synchrotron at room temperature and then SEM analyses were conducted. Figure 9 shows the SEM image of the sample along with X-ray scan at room temperature.
Bright layer of few microns at the surface can be noticed from SEM image. According to X-ray diffraction, this is clearly cementite layer which already formed during boost step. Moreover, very high intensity of retained austenite peaks is an indication of high carbon content dissolved in austenite before quenching.
Based on the diffraction patterns recorded in-situ during the boost periods the carbides which are formed during the boost step for sample 1 were quantitatively analyzed using the Rietveld refinement. Only the cementite structure was used as carbide so other structures were neglected. It is assumed that all previously present carbides were dissolved at 940 °C right before the first boost step, i.e., this point was taken as a reference of zero. Figure 10 shows the amount of cementite formed during boost steps.
Cementite content evolution during boost step of sample 1 at the surface. Average deviation for each data points is approx. \( \pm \) 2 mass pct but error bars are not shown in the figure for the sake of clarity. The purpose of the graph is only to see the growth tendency of carbides rather than certain quantitative analyses
It is very important to mention that, amount of carbon content dissolved in austenite is determined by using lattice parameter which is mainly based on the peak position, not the peak intensity. However, quantitative analyses of the cementite takes account peak intensity. Between the steps, the peak intensities slightly varied due to thermal expansion or shrinkage of the material. Although these variations were not high, it might still affect the peak intensity of minority phases significantly and give difference in the quantitative results. For this reason, regarding the results presented in Figure 10 only the evolution of the cementite formation should be assessed instead of the absolute values.
Carbides started to form already in very early stages so carbide formation rate is higher than the dissolution rate. After 30 seconds of the first boost step, the carbide dissolution rate, balanced with the carbide formation rate which causes amount of cementite to stay constant. The reason of this might be high driving force of carbide dissolution triggered by the steep carbon gradient. Because during the other two boost steps, the amount of carbides increases gradually over time. It can be seen that the carbide formation rate during the third boost step is much higher than first two due to the higher initial carbon content being close to the solubility limit.
4.2 Diffusion and Hardening Steps
The carbon gradient built up in the material is extremely large in the boost steps and this leads to very high potential differences, which afterward result in the redistribution of the carbon along the gradient. Figure 11 shows the change of carbon content calculated by Eq. [1] on the base of the measured lattice parameter of austenite for two samples during the following diffusion steps after each boost steps. For sample 1, the beam position was kept constant directly at the surface (Figure 11(a)); while for sample 2, continuous scanning from the surface to a depth of about 0.5 mm was applied with a rate of approximately 4 µm/s. By this means the carbon content directly at the surface (sample 1) and also carbon content distribution over the depth (sample 2) could be observed.
Change of average carbon content at the top surface of sample 1 (a) and carbon content in depth distribution up to a depth of 0.5 mm for sample 2 (b) where D1, D2 and D3 are diffusion 1, diffusion 2 and diffusion 3, respectively. Final surface carbon contents of 0.68 pct for sample 1 and 0.66 pct for sample 2 after hardening are shown with horizontal dashes
Since the carbon gradient was very high at the beginning of the diffusion step, the driving force for diffusion was also high. Thus, carbon diffused faster at early stages and slowed down afterward, which created an expected rate decrease in the overall graph for both samples. Therefore, graphs are getting flatter with increasing time. The initial carbon content of all samples was 0.2 pct and after three boost and diffusion cycles a final carbon content of 0.76 pct and 0.74 pct was reached directly at the surface for sample 1 and sample 2, respectively. The temperature was reduced to 840 °C in the hardening step, and subsequently the samples were quenched from this temperature. During the hardening step, the carbon contents further reduced to 0.67 pct and 0.65 pct for sample 1 and for sample 2, respectively. The final carbon contents at the end of the hardening step is shown with horizontal dots in Figure 11. The graphs show that the carbon content of both samples followed the same trend and gave very close results during the whole process. This observation again proved the repeatability of the experiment.
As it can be seen from graph D1 of Figure 11(b) the carbon content reached 0.2 pct in about 250 µm after 2 minutes, i.e., carbon did not diffuse all the 0.5 mm depth range, yet. In the following cycles, the carbon profile started to form. Moreover, especially for D1, area under the curve which is a representation of total carbon content increases, although there is no carbon donor gas. The reason of this is attributed to the dissolution of carbides and monolayer of carbon formed during boost step, which acts as an extra carbon supply at the beginning of diffusion step. On the other hand, in the second (D2) and third (D3) diffusion step, the carbon content at 0.5 mm depth gradually increased up to about 0.37 and 0.45 pct, respectively. Moreover, it can be noticed that, unlike the D1, area under curve reduces which can be explained by the fact that carbon content diffused deeper than the probed depth of 500 µm. Additionally, the rate of carbon content decreases at the surface and the rate of carbon content increase at 500 µm depth is quite different. This indicates that carbon diffusion slows down through the depth due to lower driving force.
If early stages of the diffusion steps of sample 1 is examined closely, a slight increase in the carbon content in the first 10 seconds would be noticeable, even though there is no presence of acetylene gas anymore. After this increase, carbon content either stays constant or reduces slowly. Figure 12 shows the carbon content evolution for the first two minutes of all three diffusion steps of sample 1.
The reason of this slight increase of the carbon content in the first 10 seconds of the diffusion phase is most probably shrinkage of the sample due to the temperature drop. During transition from the boost step to the diffusion step, the vacuum control valve opens to remove the remaining acetylene gases inside the chamber. Creation of sudden gas flow cause temperature to decrease couple of degree in a very short time. Therefore, the peak shifts slightly to the top of the sample that contains the higher carbon due temperature related shrinkage of the sample. Thus, this increase is not considered as a material related phenomena.
Afterward, it is normally expected that the carbon content decreases again since carbon diffuses through the depth of the sample. However, carbon content of all steps stays constant for about 1 minute. The reason of this equilibrium might be that there is an extra carbon supply to the surface in absence of acetylene. As it is mentioned before, this carbon supply can be dissolution of cementite and/or absorption of carbon atoms accumulated at the surface during previous boost steps. After the first minute passed, the carbon diffusion rate overpasses the carbon supply rate; therefore, the carbon content in solution with austenite decreases due to the diffusion of carbon atoms into the depth of the sample. To support this hypothesis, cementite contents during the first two minutes of each diffusion step were determined and showed in Figure 13. Since the amount is very low, the values fluctuate especially for the first diffusion step. In the first 60 seconds, there is an increase in cementite content for the second and the third diffusion step, which is possibly because of carbon atoms that were accumulated at the surface during the previous boost steps. This accumulation still supplies carbon to the surface by which the effect of the boost step still continues, although there is no gas in the chamber. This kept the carbon content at the surface stable for a while and caused more cementite formation. For the step diffusion 1, however, cementite content still stay constant at approximately the same value as indicated in Figure 10.
After a first minute passed, cementite content for all diffusion steps start to decrease. This is almost the same point where steady-state condition of carbon in austenite ended in Figure 12. Therefore, the effect of the boost step as precipitation of carbides might still continue in the early stages of the diffusion step.
4.3 Quenching Step
In this in-situ experiment the quenching rate was achieved through a high-pressure helium flow, i.e., the quenching rate is not constant with time. The quenching rate was 30 °C/s in the first 10 seconds and reduced exponentially until 90 °C was reached. Below that temperature, the helium quench gas was stopped and the samples cooled slowly down to room temperature.
The quenching step of sample 1 was examined in detail. Rietveld analysis of the diffraction patterns during quenching to room temperature provided a precise evolution of phase fractions in the near-surface region vs. the temperature as displayed in Figure 14.
The graph in Figure 14 indicate that no transformation occurs at the surface until the martensite start temperature (Ms) is reached despite the moderate cooling rate. Based on the in-situ data the martensite start temperature was determined at about 205 °C. The reason that no further transformation was observed might be due to the high carbon content in the case that retarded the bainite transformation in the near-surface region.
Based on the experimentally determined Ms temperature the carbon content dissolved in austenite before quenching can be determined using Eq. [2] that was developed by van Bohemen for conventional steels with 0.1-1.9 pct carbon and less than 7 pct in total of other alloying elements.[36] According to the model, Ms can be determined by,
where \( \mathop \sum \limits_{i} K_{i} x_{i} = 31x_{\text{Mn}} + 13x_{\text{Si}} + 10x_{\text{Cr}} + 18x_{\text{Ni}} + 12x_{\text{Mo}} \) describes the effect of mass percent of other substitutional elements. Applying 205 °C for the Ms—temperature the carbon dissolved in austenite can be calculated to about 0.73 pct. This value correlates well with the final carbon content obtained by EMPA as given in Figure 5; however, the carbon content determined from Onink’s formula based on the lattice parameter of austenite gives a value of approximately 0.67 pct at the end of hardening at 840 °C right before quenching. This 0.06 pct difference corresponds to a difference in the Ms—temperature of about + 17 °C. It is known that, a difference in defect structure of austenite and austenite grain size can shift the Ms temperature of the same material.[36,37,38,39] Furthermore, the thermal expansion coefficient of face-centered cubic (FCC) lattice deviates from linearity when temperature reduces[40]. Consequently, this difference is within the combinations of error margins of two mathematical calculations so it is acceptable.
The in-situ diffraction data also offer the possibility to determine the carbon content in solution in the martensite based on the lattice parameters. In Reference 41, a linear relationship between the tetragonality of martensite and the carbon content in martensite was given by
Other alloying elements such as chromium and manganese substitute iron so they only have a minor effect on c/a ratio of martensite. Since the ratio of both lattice parameters is considered, effects of temperature are mostly self-compensating.[42,43] In Figure 15 the evolution of the determined lattice parameters as well as of the carbon content in martensite calculated using Eq. [3] both plotted vs. the temperature is presented.
Evolution of lattice parameters of martensite and of the carbon content in solution for martensite for sample 1 as a function of temperature. Carbon content is calculated based on the average lattice parameter values, i.e., the error bars are neglected. The dotted vertical lines show the amount of martensite in mass pct at the top and the time from the beginning of quenching in seconds at the bottom
In the early stages of transformation the lattice parameters determined from in-situ diffraction data show high standard deviations since the amount of martensite is rather low. In the first 3 seconds, until 185 °C, the lattice parameter “c” increases steeply and then stays almost constant, while the lattice parameter “a” decreases with also high rate in the first 3 seconds and then continue to decrease with a very low rate. After the first minute, both values stay constant until the end of the quenching step.
The tetragonality of the martensite, i.e., the c/a ratio, increases during the transformation in a way that first 17 pct of martensite, which is formed within the first 5 seconds, has a lower c/a—ratio than later formed martensite. Between 3rd and 5th seconds, measurements and fits are more precise due to higher amount of martensite. One possible reason might be the preferential transformation of regions with lower carbon content, for example near precipitates or near grain boundaries. This may also be an indication that carbon atoms were not evenly distributed in the measured area during the diffusion and hardening steps. On the other hand, the behavior in the early stages could be attributed to a phenomenon of direct ordering of carbon atoms within the lattice at high temperature (Zener ordering), as well as an instantaneous self-tempering effect of martensite, which is more pronounced in the first stage of the transformation due to the higher temperature.[44,45] Final possible reason could be second order stresses between the austenite and the martensite, leading to high local strains, therefore influencing the lattice parameters. Additionally, if also the lattice parameter change of austenite is examined as displayed in Figure 16, it can be noticed that a deviation from linear contraction takes place below Ms, while the change of lattice parameter in the high temperature range follows thermal expansion coefficient determined as 21.2 × 10−6 K−1, which is well agreeing with previous studies.[46,47] The deviation to lower values in connection with the martensitic transformation has already been observed in medium and high carbon steel and the effect could be attributed to the generation of high hydrostatic compressive stresses in austenite,[48] which can also be coupled with carbon partitioning.[15,45,49]
Also for the quenching step the presented results indicate that the in-situ diffraction analysis using the newly developed process chamber is well suited to monitor the phase transformation kinetics and the evolution of the lattice parameters of the phases during LPC at high spatial and temporal resolution. However, care must be taken regarding the assessment of the results.
In the case of martensitic transformation, which involve both chemistry and internal stress changes, the XRD study alone is generally limited to semi-quantitative conclusions based on assumptions for measurement of the carbon content. Therefore, determination of the exact carbon content of all phases in order to make a certain judgment about the carbon partitioning kinetics is not ideal. Nonetheless, if the XRD results are combined with literature studies that are based on complementary characterization techniques, reliable statements about the microstructural mechanisms can be deduced.
Transformation of martensite is usually believed to occur without diffusion of interstitials, i.e., carbon partitioning is usually neglected because of very low temperatures and short times. Previous studies, however, exhibit evidences about carbon partitioning from martensite to retained austenite during quenching.[50,51,52,53,54] Depletion of martensite during cooling is highly dependent on the cooling rate. It was studied that cooling rates below 25 K/s are highly favorable for carbon partitioning from martensite to retained austenite.[52] In the present in-situ study, the average cooling rate from hardening temperature (840 °C) to Ms—temperature was about 17 K/s and further reduced to lower values below Ms. Although the cooling rates somehow correlate, the Ms temperature given in literature are quite higher, i.e., relatedly carbon mobility during quenching is greater compared to the present study. However, there are also some studies in which minor effect of carbon partitioning from martensite to retained austenite could be observed for Ms temperature down to 200 °C.[44]
Besides the redistribution of carbon from martensite to retained austenite, carbon segregation to microstructural features like dislocations or martensite lath boundaries is also very common in literature, especially for the cases that lower Ms temperature restricts the mobility of carbon.[55,56,57] Therefore, based on the combination of the present results and results from literature, carbon partitioning from supersaturated martensite to microstructural features during martensitic transformation is most convincing among others. However, it should be kept in mind that carbon partitioning from martensite to retained austenite is also possible to a small extend.
5 Conclusions
An experimental heat treatment chamber with a related control system was developed to perform in-situ X-ray diffraction experiments during complete LPC process. Phase contents, carbon and micro-hardness profiles of samples carburized in the experimental chamber in the final state were compared with results determined by using an industrial furnace. Despite some slight differences in the two heat treatment set-ups the results were very close to each other. By this means, it was proved that the newly developed chamber is reliable to perform an industry-like LPC treatment at small scale.
Synchrotron X-ray diffraction experiments were conducted at the high energy synchrotron beamline P07-EH3 of the Petra III ring at DESY/Hamburg during the whole LPC process and final quenching. Received data were analyzed by using the convolution-based Rietveld refinement and experimental based mathematical calculations to obtain information about the microstructural evolution. All findings based on those data lead to the following conclusions:
-
1.
The austenite saturation limit is reached within seconds of the boost steps due to very fast carbon uptake rate from atmosphere into sample. Carbon atoms accumulate at the surface and carbides rapidly precipitate. Therefore, carbon diffusion from the atmosphere to the surface is decelerated. After that point, which lasted about 20 second, the carburizing reaction changes from an atmosphere dominated to a material dominated, so further carbon transfer from the atmosphere to the surface is controlled by both cementite dissolution and diffusion of carbon through cementite in the depth. Therefore, increasing the duration of boost step to very long times does not directly increase the carbon profile; instead, this would only increase the amount of carbides formed at the surface, and possibly grain boundaries, which will contribute to the carbon profile by dissolution in following steps.
-
2.
Carbides, mainly cementite, formed at the surface of the material during in the early seconds of the boost steps start to dissolve in the following diffusion steps. The formation and dissolution kinetics of the carbides highly depend on the amount of carbides and on the base carbon content in the austenitic matrix. When the number of boost step increases the stability of cementite also increases. Thus, the amount of cementite formed in the first boost step stayed constant, while cementite formed on the second and the third boost step continued to increase even until the end of first minute of the following diffusion steps.
-
3.
In the early minutes of all diffusion steps, carbon content stayed constant. It is observed during that period that the cementite content continues to increase for the second and the third boost steps although there is no presence of the carbon donor gas. This effect is attributed to the high carbon accumulation at the surface during the boost steps. Until this accumulation was fully consumed, the carbon supply to the surface continued.
-
4.
During quenching, early formed martensite, especially martensite that was formed in first 5 seconds, had lower c/a ratio than later formed ones. This difference was attributed to the early phase transformation of austenite grains having lower carbon content. On the other hand, instantaneous self-tempering, second order stresses between austenite and martensite, and carbon redistribution/ordering leading to lower tetragonality are expected. This is confirmed by the observed final carbon content of the martensite which was lower than the carbon content determined in the austenite right before the quenching phase. The reason of this difference was attributed to not only the uneven carbon distribution, but also to the carbon partitioning during transformation. As no transition carbides could be observed in the diffraction pattern after quenching, this lead to the conclusion that carbon partitioning to austenite in low extent and carbon segregation to microstructural features such as dislocations, grain boundaries or martensite lath boundaries take place directly during the martensitic transformation.
Data Availability
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.
References
1 E.J. Mittemeijer and M.A.J. Somers: Thermochemical Surface Engineering of Steels: Improving Materials Performance, Woodhead Publishing., Cambridge, 2015, pp 485-553
2 B. Clausen, E. Hoffmann, and H.W. Zoch: HTM - J. Heat Treat. Mater., 2008, vol. 63, pp. 326–36.
3 A. von Starck, A. Mühlbauer, and C. Kramer: Handbook of Thermoprocessing Technologies: Fundamentals, Processes, Components, Safety, Vulkan-Verlag GmbH, 2005.
M. Steinbacher: Universität Bremen, PhD Thesis 2012.
D.H. Herring and R.V. Peters Jr.: Gear Technol.
6 H. Altena and F. Schrank: HTM - Haerterei-Technische Mitteilungen, 2002, vol. 57, pp. 247–56.
7 H. Altena: HTM – Härterei Tech. Mitteilungen, 1994, vol. 49 (1), pp. 58–63.
8 K. Yada and O. Watanabe: Comput. Fluids, 2013, vol. 79, pp. 65–76.
9 R. Gorockiewicz: Vacuum, 2011, vol. 86, pp. 448–51.
10 M.Y. Semenov, A.E. Smirnov, and M.Y. Ryzhova: Met. Sci. Heat Treat., 2013, vol. 55, pp. 38–42.
11 M. Steinbacher, B. Clausen, F. Hoffmann, P. Mayr, and H.W. Zoch: HTM - Haerterei-Technische Mitteilungen, 2006, vol. 61, pp. 186–94.
12 H. Ikehata, K. Tanaka, H. Takamiya, and H. Mizuno: ISIJ Int., 2012, vol. 52, pp. 1348–55.
13 V.A. Esin, B. Denand, Q. Le Bihan, M. Dehmas, J. Teixeira, G. Geandier, S. Denis, T. Sourmail, and E. Aeby-Gautier: Acta Mater., 2014, vol. 80, pp. 118–31.
14 M. Villa, K. Pantleon, and M.A.J. Somers: J. Alloys Compd., 2013, vol. 557, pp. 543–8.
J. Epp, T. Hirsch, and C. Curfs: Metall. Mater. Trans. A Phys. Metall. Mater. Sci., 2012, vol. 43, pp. 2210–17.
16 F. Niessen, M. Villa, F. Danoix, J. Hald, and M.A.J. Somers: Scr. Mater., 2018, vol. 154, pp. 216–9.
17 J. Feugeas, B. Gómez, and A. Craievich: Surf. Coatings Technol., 2002, vol. 154, pp. 167–75.
18 J.C. Oxley, J.L. Smith, F.L. Steinkamp, J. Gorawara, and V. Kanazirev: J. Chem. Heal. Saf., 2017, vol. 24, pp. 26–33.
19 G. Ashiotis, A. Deschildre, Z. Nawaz, J.P. Wright, D. Karkoulis, F.E. Picca, and J. Kieffer: J. Appl. Crystallogr., 2015, vol. 48, pp. 510–9.
20 A.A. Coelho: J. Appl. Crystallogr., 2018, vol. 51, pp. 210–8.
21 J. Epp, J. Dong, H. Meyer, and A. Bohlen: Scr. Mater., 2020, vol. 177, pp. 27–31.
22 M. Onink, C.M. Brakman, F.D. Tichelaar, E.J. Mittemeijer, S. van der Zwaag, J.H. Root, and N.B. Konyer: Scr. Metall. Mater., 1993, vol. 29, pp. 1011–6.
B. Esper: Ind. Heat., 2009, N.p.
D.H. Herring: Therm. Process., 2012, N.p.
M. Sugiyama, K. Ishikawa, and H. Iwata: Adv. Mater. Process. 1999, vol. 155, pp H29–H33.
26 R.J. Madix: Adv. Catal., 1980, vol. 29, pp. 1–53.
27 R. Neubauer, C.M. Whelan, R. Denecke, and H.P. Steinrück: J. Chem. Phys., 2003, vol. 119, pp. 1710–8.
R. Byron Bird Warren E. Stewart Edwin N. Lightfoo, R.B. Bird, W.E. Stewart, and E.N. Lightfoot: Transport Phenomena, Revised 2nd Edition, John Wiley & Sons, Inc, Hoboken, 2006, pp. 580-657.
29 P. Kula, R. Pietrasik, and K. Dybowski: J. Mater. Process. Technol., 2005, vol. 164–165, pp. 876–81.
C. Sauerborn: Shak. Verlag, PhD Thesis, 2008.
31 J. Agren: Scand. J. Metall., 1990, vol. 19, pp. 2–8.
32 J. Ågren and G.P. Vassilev: Mater. Sci. Eng., 1984, vol. 64, pp. 95–103.
33 C. Wert and C. Zener: J. Appl. Phys., 1950, vol. 21, pp. 5–8.
34 A. Schneider and G. Inden: Calphad Comput. Coupling Phase Diagrams Thermochem., 2007, vol. 31, pp. 141–7.
35 B. Ozturk, V.L. Fearing, J.A. Ruth, and G. Simkovich: Solid State Ionics, 1984, vol. 12, pp. 145–51.
36 S.M.C. Van Bohemen: Mater. Sci. Technol., 2012, vol. 28, pp. 487–95.
A.S. Sastri and D.R.F. West: J. Iron Steel Inst., 1965.
P.J. Brofman and G.S. Ansell: Metall. Trans. A, Phys. Metall. Mater. Sci., 1983, vol. 14 A, pp. 1929–31.
C. Celada-Casero, C. Kwakernaak, J. Sietsma, and M.J. Santofimia: Mater. Des., 2019, vol. 178, N.p.
40 S.M.C. Van Bohemen: Scr. Mater., 2013, vol. 69, pp. 315–8.
41 H.K.D.H. Bhadeshia and R.W.K. Honeycombe: Steels: Microstructure and Properties: Fourth Edition, Butterworth-Heinemann Elsevier Ltd, Oxford, 2017, pp. 135-177.
42 Y. Lu, H. Yu, and R.D. Sisson: Mater. Sci. Eng. A, 2017, vol. 700, pp. 592–7.
Y. Lu, H. Yu, X. Cai, Y. Rong, and R.D. Sisson: in 23rd International Federation of Heat Treatment and Surface Engineering Congress 2016, IFHTSE 2016, 2016, pp. 404–9.
J. Epp: Universität Bremen, PhD Thesis, 2016.
J. Epp: in Residual Stresses 2016: ICRS-10, Materials Research Proceedings 2, 2017, pp. 283–88.
46 Y. Wang, Y. Tomota, T. Ohmura, S. Morooka, W. Gong, and S. Harjo: Acta Mater., 2020, vol. 184, pp. 30–40.
47 P. Huyghe, M. Caruso, J.L. Collet, S. Dépinoy, and S. Godet: Mater. Sci. Eng. A, 2019, vol. 743, pp. 175–84.
M. Villa, F. Niessen, and M.A.J. Somers: Metall. Mater. Trans. A Phys. Metall. Mater. Sci., 2018, vol. 49, pp. 28–40.
J. Epp: in 23rd International Federation of Heat Treatment and Surface Engineering Congress 2016, IFHTSE 2016, 2016.
50 H.K.D.H. Bhadeshia: Met. Sci., 1983, vol. 17, pp. 1–2.
M. Sarikaye, G. Thomas, J.W. Steeds, S.J. Barnard, and G.D.W. Smith: 1982, N.p.
D.H. Sherman, S.M. Cross, S. Kim, F. Grandjean, G.J. Long, and M.K. Miller: Metall. Mater. Trans. A Phys. Metall. Mater. Sci., 2007, vol. 38, pp. 1698–1711.
53 C. Lerchbacher, S. Zinner, and H. Leitner: Micron, 2012, vol. 43, pp. 818–26.
54 R.C. Thomson and M.K. Miller: Scr. Metall. Mater., 1995, vol. 32, pp. 149–54.
55 J. Wilde, A. Cerezo, and G.D.W. Smith: Scr. Mater., 2000, vol. 43, pp. 39–48.
56 C. Zhu, A. Cerezo, and G.D.W. Smith: Ultramicroscopy, 2009, vol. 109, pp. 545–52.
57 L. Morsdorf, C.C. Tasan, D. Ponge, and D. Raabe: Acta Mater., 2015, vol. 95, pp. 366–77.
Acknowledgments
Open Access funding enabled and organized by Projekt DEAL. The authors gratefully acknowledge the support from the Deutsche Forschungsgemeinschaft (DFG) for funding this research under the collaborative project EP-128/2-1- | GI-376/15-1 (DFG project no. 399551201), Deutsches Elektronen-Synchrotron (DESY) for granting beam time and Dr. Norbert Schell for technical and scientific support during the beam time. Furthermore, the authors would like to thank Alexander Kohl and Sebastian Ohneseit for their participation in the measuring campaign at DESY and in particular Alexander Kohl for his engagement in the planning and realization of the process chamber.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Manuscript submitted October 12, 2020; accepted January 28, 2021.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tapar, O.B., Epp, J., Steinbacher, M. et al. In-Situ Synchrotron X-ray Diffraction Investigation of Microstructural Evolutions During Low-Pressure Carburizing. Metall Mater Trans A 52, 1427–1442 (2021). https://doi.org/10.1007/s11661-021-06171-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-021-06171-2