Abstract
With the flux of high-energy, deeply penetrating X-rays that a 3rd-generation synchrotron source can provide and the current generation of large fast area detectors, the development and use of synchrotron X-ray methods have experienced impressive growth over the past two decades. This paper describes the current state of an important subset of synchrotron methods—high-energy X-ray diffraction employing in situ loading. These methods, which are known by many acronyms such as 3D X-ray diffraction (3DXRD), diffraction contrast tomography (DCT), and high-energy X-ray diffraction microscopy (HEDM), have shifted the focus of alloy characterization to include crystal scale behaviors in addition to microstructure and have made it possible to track the evolution of a polycrystalline aggregate during loading conditions that mimic alloy processing or in-service conditions. The paper is delineated into methods for characterizing elastic behavior including measuring the stress tensor experienced by each crystal and the inelastic response including crystal plasticity, phase transformations, and the onset of damage. We discuss beam size and detector placement, resolution, and speed in the context of the spatial and temporal resolution and scope of the resulting data. Work that emphasizes material models and the interface of data with various numerical simulations and machine learning is presented.
Similar content being viewed by others
1 Introduction
Three-dimensional characterization methods have advanced quantitative understanding of the structures, phenomena, and behaviors that are most important for metallic alloy processing and performance design—but there is much yet to learn, even about the processes that seem simplest. Crystal scale elasticity is inherently anisotropic and three-dimensional and produces the stress fields that drive many of the other important and interesting deformation and damage phenomena in a loaded polycrystal. As the load increases, crystal scale yielding seems to initiate at high stress regions, then to spread in often non-intuitive ways; an evolution in yield strength is intimately coupled to an increase in stress. Plasticity, another anisotropic deformation phenomena and the source of the increased strength, is a collection of dynamic (hence, the term “plastic flow”) processes that seem homogeneous and steady when viewed from the perspective of a deforming polycrystalline tensile sample or through the filter of the macroscopic stress-strain curve, but must vary from one crystal to the next and proceed in a stop/start manner in time. The initiation of fatigue cracks and voids that will eventually limit the useful life of a metallic component seem stochastic when viewed from the macroscale but are a direct result of the local material state and applied stress conditions. The fastest developing class of three-dimensional characterization experiments capable of understanding crystal and subcrystal scale deformation and damage processes are those being conducted at high-energy X-ray beamlines at synchrotron sources around the world. This paper summarizes the state of these high-energy X-ray diffraction (HEXD) experiments and presents examples, focusing specifically on the use of in situ mechanical loading methods.
Diffraction is one of the oldest X-ray characterization methods used on metals. The enormous flux of deeply penetrating high-energy X-rays at a modern (3rd generation) synchrotron light source has spawned an entirely new class of X-ray based characterization experiments that enable interrogation of every individual crystal within a bulk polycrystalline aggregate. Advancements in the development of large, fast, two-dimensional X-ray detectors and sophisticated in situ loading stages have also driven the recent surge of HEXD development specifically for understanding the behavior and evolving structure of deforming polycrystalline metals cf.[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] Traditionally, understanding is gained using a variety of probes to form metallographic images of the internal structure within a metal. Grain morphology and microstructure continue to play important roles in HEXD characterization—something we will refer to as real space topology. However, within the diffracted X-ray intensity data from each crystal, there is also reciprocal space information related to the configuration and distortion of its unit cell. This enables the quantification of the lattice orientations and the lattice strain and stress tensors within a crystal.
This paper describes recent developments in the area of grain-specific synchrotron X-ray diffraction experiments done on bulk metallic samples being loaded in situ at the beamline. We delineate descriptions of the work by the behavior that it illuminates elastic straining (stress determination) and inelastic, post-yield behavior including plasticity and some related stress-induced phase transformations. We begin with a general description of this specific class of HEXD experiments followed by the review of recent work. Instead of an exhaustive review, we focus on examples illustrating the kinds of behaviors that can be characterized during in situ loading.
2 Background
The attributes of high-energy (typically \(>50\ \hbox {keV}\)) synchrotron X-ray beams that make them ideal for understanding metals are their short wavelength—for deep penetration within metallic samples—and enormous flux, to enable non-destructive measurements of bulk response with up to microsecond time resolution. HEXD is the most general classification of diffraction experiments that can be employed at a high-energy beamline. The focus of this paper is on monochromatic X-ray methods capable of interrogating each crystal (or subcrystal) individually during in situ loading. In the literature, these methods are known as 3 Dimensional X-ray diffraction (3DXRD),[1] diffraction contrast tomography (DCT)[17,18], or high-energy diffraction microscopy (HEDM). The differences between the methods, in general, are not important for this paper. The emphasis is on high-energy X-ray diffraction with in situ loading, so we will use in situ HEDM to refer to this general class of experiments; when it is relevant, we call out some of the specific acronyms. Simply put, in situ HEDM employs the Bragg-diffracted intensity from individual crystals or subvolumes of individual crystals within a polycrystalline aggregate to understand the state of the material within the diffraction volume (grain topology, orientation, lattice strain, and phase content) at crystalline and now subcrystalline scales. By loading the sample in situ, this state can be quantified as it evolves.
2.1 The Diffraction Experiment
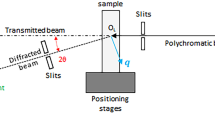
Detailed descriptions of in situ HEDM experiments, including data reduction, can be found in the cited references. Our intent here is to present the attributes of the methods and resulting data in a way that elucidates the “philosophy” behind a particular in situ HEDM experiment and, more importantly, what kinds of physical insights might be ascertained from the data. Bragg diffraction is governed by Bragg’s law, \( n\lambda = 2d\,{\text{sin}}\theta \). Here n is an integer, \(\lambda \) is the X-ray wavelength, d is the spacing between two planes of atoms, and \(\theta \) is the diffraction angle. A typical in situ HEDM experiment is shown in Figure 1. The point of intersection of a diffracted beam of X-rays on the 2D area detector can be parameterized by the angular “polar coordinates,” 2\(\theta \) and \(\eta \). By rotating the specimen and, at times the entire load frame, by the angle \(\omega \) about the loading axis (a process we will refer to in this paper as an \(\omega \) scan), each lattice plane within every crystal in the diffraction volume can be brought into the Bragg diffraction condition. So each diffraction point on the detector can be parameterized with three angles: the coordinates on the detector, \(2 \theta \) and \(\eta \) and the rotation angle, \(\omega \).
The interpretation of diffracted intensity measured on an area detector depends heavily on the sample to detector distance, D. As the detector is moved closer to the specimen, the distribution of diffracted intensity on the detector is dominated by the real space locations of scattering volumes in the specimen. As the detector is moved farther from the specimen, the data tend towards a mapping of reciprocal space—sensitive to differences in lattice plane spacing and orientation. This is illustrated schematically in Figure 2.
Four different variations of HEDM have developed to take advantage of detector placement sensitivities to microstructural features in real space and reciprocal space. (i) Near-field HEDM (nf-HEDM) places the detector close to the sample (\(<10\ \hbox {mm}\)) to maximize sensitivity to real space. Detectors chosen for these measurements are often X-ray scintillators paired with optical cameras and magnifying lenses to minimize effective pixel size and maximize spatial resolution. The spatial distribution of grains as well as their shape and boundaries can be determined with the near-field method. Note that DCT experiments are also conducted at these distances. (ii) Far-field HEDM (ff-HEDM) places a large-panel, direct detection area detector approximately 1 m away from the specimen. In this configuration, large regions of reciprocal space can be probed relatively quickly and grain-average quantities, including the elastic strain and orientation, can be determined for hundreds to thousands of grains in single scans. Near- and far-field HEDM were the detector distances laid out originally for HEDM (3DXRD)[1] and have become the workhorse methods at many high-energy beamlines, but additional experiments have been developed to take advantage of other configurations. (iii) Very far-field HEDM places a high dynamic range detector over 3 m away from the specimen.[19,20,21,22,23] The goal of this approach is to provide sufficient sample to detector distance to separate diffracted intensity from individual subvolumes of crystal so that their micromechanical responses can be probed individually. A detector with wide-dynamic range (but usually accompanied by a relatively small active detection area) enables the simultaneous probing of subvolumes spanning multiple orders of magnitude. (iv) Mid-field HEDM (mf-HEDM) is the most recent approach being developed.[24] In this configuration, a balance between real and reciprocal space resolution is sought, with reconstructions of thermo-mechanical response of very small subvolumes of crystals (\(<\mu \hbox {m}\)) now possible. Table I summarizes the detection capabilities described. We note that detector technologies are constantly evolving with faster collection times, larger active areas, and higher dynamic ranges so the table reflects current detector considerations.
Schematic depicting how the diffracted intensity from three slightly misoriented subvolumes within a crystal would appear on detectors at various distances. The total spacing of the subvolumes is \(\varDelta \varvec{p}\) and the projected misorientation is \(\varDelta \eta \). The approximate active detection area at each distance is noted, in addition to the approximate detector placement typically employed for each measurement regime
2.2 In Situ Loading
The details of how specimens are loaded during an in situ HEDM experiment are just as important as the X-ray diffraction. The design of the load frame and the configuration of the positioning setup must take into account loading and the X-ray trajectories. The “stress rigs” inherited from neutron diffraction have evolved into sophisticated, well aligned mechanical testing environments, designed for loading a “bulk” mechanical testing sample—containing many thousands of crystals within its gage section—that mimics processing and in-service conditions of a metal, while enabling unimpeded illumination and diffraction from the gage section. Many load frames have been developed for HEXD experiments (HEDM and powder experiments) over the past 2 decades. Some HEDM-specific systems of particular note include the following: (i) The RAMS series of loading machines which have placed a special emphasis on creating the clearance and precision for 360 deg ω rotations axis during monotonic and cyclic loading,[25] (ii) the nanox system that was designed to load a specimen during a topotomography experiment—which rotates about a specific scattering vector[26], and (iii) the implementation of a commercial planar-biaxial loading system for introducing multiaxial macroscopic stress states.[27] In addition to custom load frames, in situ HEDM has been made possible by a collective community effort driving improvements in data reduction/reconstruction algorithms cf.[13,28]
3 Elastic Strain and Stress Evolution
From the earliest uses of X-ray diffraction, observing the elastic response of crystalline materials has been a part of the diffraction experimental repertoire. Lattice strain due to a mechanical load is just the engineering strain component normal to a set of lattice planes, \( \epsilon = {\text{ }}\Delta d/d_{{\text{o}}} \), where the change in lattice spacing, \(\varDelta d\), can be determined from the peak position before and after loading and \(d_{\text{o}}\) is the unstrained lattice spacing. The lattice strains for every peak in an in situ HEDM dataset can be determined in a very efficient manner. The elastic lattice strain tensor for a particular crystal (or subcrystal) can be computed using six or more independent lattice strains. Using the single crystal elastic moduli, the crystal stress can then be computed. The measurement of crystal scale lattice strains and subsequent computation of the stress state being experienced by every individual crystal inside a deforming aggregate that has been made possible with in situ HEDM experiments. As illustrated in this section, this has fundamentally changed the way mechanical testing data are used to understand the micromechanical behavior of polycrystalline metals. Instead of using pre- or post-deformation images from the microscale to infer and possibly explain macroscopic mechanical behaviors, extracting the stress–strain response directly from the microscale in real time is now possible. As will be shown, images (tomographic or near field) can be superimposed onto stress field information, in some cases, to better understand real space topology. Of particular focus in this section of the paper, are experimental studies exploring the interplay between mechanical anisotropy due to crystal orientation, boundary conditions imposed by neighboring grains, and the evolution of flow stress due to local defect evolution.
We are careful to differentiate studies that have quantified lattice strains from peak shifts in HEDM data from those that compute stress, as there are subtle, but critical, differences between the two. A lattice strain or a lattice strain distribution can be used with additional information to understand the general state of a material but the stress tensor is one of the most fundamental quantities used in the design of mechanical components and in metals processing design and needs at least 6 lattice strains to compute. Many of the important properties and performance measures of structural alloys on the macroscale are directly related to the transmission and concentration of load through isolated regions of material on the crystal scale, often revealing themselves as regions of damage initiation in post-mortem microscopy. As such, the ability to quantify both the spatial heterogeneity and the evolution of stress at the grain-scale during in situ loading is a major advance in the study of alloy micromechanical response.
In this section, we describe progress on using in situ HEDM for understanding elastic strains and stresses beginning with early discoveries about crystal scale stress state variation and the progress made for quantifying stresses with more crystals within the aggregate. We describe some of the applications that have been explored recently using these new tools. Then, we present some of the most recent work investigating stress transients using continuous loading and the new generation of high-speed detectors for high-energy X-rays. Finally, we point to the future of stress measurements by describing methods capable of subcrystal stress resolution. Because of the geometry of the HEDM experiment, the nf-HEDM/DCT configuration is a challenging one for lattice strains. However, these data are spatially resolved so some DCT results using high modulus materials are presented in the subcrystal resolution section.
3.1 The Stress States of Individual Crystals
The measurement of the elastic strain (and stress) tensors experienced by individual grains embedded within polycrystals was part of the initial 3DXRD suite of measurements conducted in situ at the European Synchrotron Radiation Facility (ESRF) in the early 2000s.[29,30,31] Importantly, these strain measurements were made possible by the ability to associate subsets of the diffraction peaks captured on the detector from a polycrystal with a specific crystal—a process referred to as indexing.[1] These early experiments were truly “heroic efforts” designed to track the evolution of elastic strains and stresses in a few grains within the deforming aggregate. In some cases lattice strain measurements were combined with structure-based simulations to quantify fundamental crystal scale properties like the single crystal elastic moduli, for instance.[32] The variation of stress state from crystal to crystal and the non-coaxiality of crystal stress states with the macroscopic uniaxial stress being applied to the specimen was established.[10] Figure 3 depicts the macroscopic loading curves for in situ HEDM experiments conducted on Ti-7Al in two states: air cooled (AC) and ice water quenched (IWQ). Clearly, these materials behave differently when viewed from the macroscale. The goal of the project was to understand the difference in crystal scale stresses within each sample. To demonstrate how those differences might be tracked, the stress state experienced by one AC crystal and one IWQ crystal within each sample are illustrated at the four points in each experiment where the diffraction measurements were taken. The full stress tensors are represented by coloring the legs of principal stress triads or “jacks” with colors consistent with the values of each principal stress. The orientation of one of the principal stress components is near the loading axis at each load but the off-axis stresses are, in most cases, non-zero. These multiaxial crystal stress states are invaluable for computing important crystal quantities like resolved shear stresses. Using diffraction-based crystal stress measures, the often-used process of predicting slip system activity for a crystal embedded within a polycrystalline tensile sample by using the Schmid factor computed using uniaxial stress has been demonstrated as being invalid.[9] Correcting the prediction of stress-induced slip has been shown to explain some observed slip system activity that might have been typified as “non Schmid”.[33] With improvements to the speed and robustness of indexing capabilities, probing the stress state of hundreds or even thousands of grain simultaneously and exploring spatial heterogeneity of load transmission in more complex loading conditions and materials have become possible cf.[34]

Reprinted from [10] with permission
(Left) Macroscopic stress–strain data for air cooled (AC) and ice water quenched (IWQ) polycrystalline Ti-7Al specimens depicting the loads where ff-HEDM experiments were conducted. (Right) Principal axis “jacks” depicting the orientation and values of the principal stress state at four indicated macroscopic stress levels (in MPa) for one crystal in the IWQ (top) and one crystal in the AC (bottom) specimens. The terms 400el and 400un refer to the data points taken at 400 MPa at the elastic–plastic transition and at unloading, respectively.
3.2 Applications
Some of the most critical stress-dependent applications have been explorations of grain-averaged stress state evolution during fracture and fatigue processes. Oddershede et. al. quantified the distribution of stress across an ensemble of several thousand grains around a loaded crack in Mg AZ31.[35] The grain stress data were then used to inform finite element modeling of stresses around the crack tip. Analyzing smooth bar low cycle fatigue, Obstalecki et al. explored the evolution of elastic strain distributions in OMC copper.[36] In another complex loading scenario, Pokharel et al. explored the evolution of stresses during the delamination between copper and tungsten phases during in situ loading.[37] Non-uniaxial macroscopic stress states have also been probed in Ti-7Al utilizing a novel in situ biaxial loading system.[38] Lastly, Naragani et al. were interested in understanding the evolution of the 3D stress field around a non-metallic inclusion within a powder metallurgy RR1000 nickel-base superalloy sample.[39] The inclusion was mapped using tomography then the sample was cyclically loaded. Figure 4 shows the evolution of the von Mises stress at various numbers of cycles. A crack (highlighted as green in the figure) was detected at 10,000 cycles.

Reprinted from [39] with permission
Evolution of the von Mises equivalent stress within a cyclically loaded RR1000 aggregate containing a non-metallic inclusion (black) at several cycle numbers measured using in situ ff-HEDM. The inset depicts the location of the crack (green) that was observed after 10,000 cycles.
In addition to loading conditions, significant work has been done to begin exploring load transmission in more realistic material systems—closer to those used in-service. Paranjape et al. examined the effects of grain interactions on the stresses that drive phase transformation in shape memory alloys using HEDM and finite element modeling.[40] Guillen et al. performed multiple experiments to explore how microstructures produced by different processing routes influenced grain stresses and expected performance in nuclear applications.[41]
3.3 Capturing Transient Stress Behaviors
Beyond spatial heterogeneity, new detector technologies are enabling studies of temporal heterogeneity of stress with increased fidelity. Of significant interest is the study of stress transients that occur across multiple time scales (from milliseconds to minutes) as polycrystals remain on the macroscopic yield surface. During a typical in situ ff-HEDM experiment, loading is halted during each \(\omega \) scan. Even though the load is manually reduced by around 10 pct during the scan to minimize creep and stress relaxation, material state evolution can still take place. Reduction in measurement time (complete 360 deg ff-HEDM \(\omega \) scans now takes minutes or less) enables the scans to be taken continuously over a specimen being loaded at small strain rates without an appreciable change in grain state during measurement. Because grain stress states no longer are moved off the single crystal yield surface, previously “hidden” stress transients have become apparent. Pagan et al. found that interactions of dislocations with ordered precipitates in Ti-7Al manifested as a flow stress decrease (softening) behavior in a subset of crystals oriented for basal and prismatic crystallographic slip.[42] Interestingly, this softening behavior was less prevalent in the same material with increasing temperature, likely due to weakening of interactions between dislocations and precipitates.[43] A continuous loading experiment of Al-Li 2099 by Tayon et al. revealed a similar softening behavior attributed to interactions between dislocations and precipitates,[44,45] with grains oriented for single slip exhibiting significantly more susceptibility to flow stress softening. Continuous scanning of specimens has also been used to monitor creep deformation. Beaudoin et al. used time series ff-HEDM data to identify “bursts” of localized stress relaxation in Ti-7Al as the microstructure reconfigured during creep loading.[46] Figure 5 shows an example.

Reprinted from [46] with permission (Color figure online)
Collective stress relaxation in grains during uninterrupted creep loading of Ti-7Al, using in situ ff-HEDM. Each grain is represented as a sphere where color corresponds to the maximum resolved shear stress for basal slip, and size indicates the decrease of the effective stress over the duration of the scan.
3.4 Intragranular Stress Resolution
Understanding load transmission in deforming bulk polycrystals can be enhanced by the quantification of elastic strain and stress fields with intragranular resolution. Many of these methods employ iterative schemes to best match the intensity collected on individual pixels of the detector and can be very computationally expensive but multiple promising paths forward are being pursued by researchers, each with different strengths and weaknesses. Juul et al.[47] and Turner et al.[48] have combined nf-HEDM orientation field reconstructions with ff-HEDM elastic strain measurements to explore transmission of stresses across grain interfaces. Ludwig et. al have employed advanced “data inversion” routines to reconstruct three-dimensional elastic strain fields in the near-field HEDM/DCT geometry[49] using a gum metal sample, capable of sustaining large elastic strains, to address the relatively modest strain resolution in the near-field data. The benefit of this method is that it takes advantage of existing experimental geometries and data reduction frameworks to begin exploring stress at subgrain length scales. At the other detector geometry extreme, very far-field diffraction (vff-HEDM) has been used to examine gradients of lattice strain components within dislocation structures.[50] The primary benefit of this method is excellent lattice strain resolution, which can approach \(10^{-5}\). Pagan and Beaudoin have developed a hybrid X-ray diffraction—finite element-based algorithm, which can take advantage of well-established lattice orientation quantification methods to reconstruct elastic strain and stress fields that are guaranteed to be in equilibrium.[51]
A particularly exciting advance for subgrain stress resolution combines point focused (”pencil-beam”) scanning tomography techniques with HEDM to reconstruct the elastic strain tensor and stress at the subcrystal length scale.[52] The physical isolation of diffraction volumes using the pencil-beam ensures increased fidelity of the reconstructed elastic strain fields. Henningsson et al. investigated various methods for reconstructing the intragranular strain fields from their pencil-beam scanning measurements.[53] Their proposed method remedied some of the inherent measurement bias by taking the spatial properties of the inverse problem into account.
4 Plasticity
Unlike elasticity, “measuring” the plastic response of a metal does not consist of quantifying a set of strains. Understanding and modeling plasticity in metals has been an active research area for over a century and the means of quantification of the plasticity experienced by a metal has been examined experimentally in a number of ways. We often connect plasticity to the non-linear stress-strain curves we see in mechanical testing data and the permanent changes we see in tensile specimen length. Of course, plasticity (crystallographic slip) is also associated with the dislocations we see in micrographs. However, one of the earliest images we have of the effects of plastic deformation is Joffe’s “röntgenogram” depicting the spreading of the Laue X-ray diffraction spot pattern (also known as asterism) from a bent rock salt sample shown in Figure 6. A diffraction peak spreads when the planes producing the peak have a spread in orientation or mosaicity. This is a natural result of being deformed by heterogeneous plastic slip. In fact, Nye’s early work on dislocations and the creation of his famous dislocation tensor was motivated by the streaks seen in diffraction data from a bent corundum single crystal.[54]

Reprinted from [55] with permission
Laue diffraction spots taken from a bent salt single crystal specimen demonstrating the spot spreading seen due to the heterogeneous plastic slip.
As shown in the schematic in Figure 2, the lattice plane orientation variation impacts the detector image differently based on distance. Three adjacent crystal subvolumes containing slightly different lattice plane orientations are shown along with the detector distances defined previously. The orientation of the normal to the lattice plane is shown as having a slight variation from one subvolume to the next—indicating schematically an orientation gradient of some kind. On the near-field detector, the physical location and distance between the subvolumes (\(\varDelta \varvec{p}\)) dominate the location of the peaks on the detector. As the detector distance increases, the peaks start to reveal differences in the azimuthal (\(\eta \)) location on the plane’s Debye–Scherrer ring (due to the slight differences in the orientation of the plane). The orientation spreading is manifested as \(\varDelta \eta \) spreading. On the very far-field detector, the intensities may actually split apart along the ring depending on the strength of the misorientation gradient. As plastic deformation proceeds, the spread in \(\eta \) seen on the detector will change as the lattice plane orientations evolve. Changes in lattice plane orientation may also induce spreading in \(\omega \), which manifests itself as a shift of intensity between adjacent detector images during an \(\omega \) scan.
The challenges and opportunities of HEDM for understanding plasticity—in the form of crystallographic slip—can be linked to the fundamental differences in the data on the various detectors shown on Figure 2. In this section, we present some of the current progress on the characterization of plasticity using in situ HEDM—highlighting the ways these different detector distances (focusing on nf, ff, and vff) have been used individually and together to extract understanding about plasticity processes at several relevant size scales. Since stress plays a fundamental role in plasticity, many of the stress quantification experiments described in the previous section were conducted concurrent with several of the experiments described here. This is a big part of the enormous opportunity and the serious data flow challenge of in situ HEDM. In addition to crystallographic slip, we also describe work on twinning and stress-induced phase transformations, which have a very different diffraction signature.
4.1 Far-Field HEDM
With the close connection between the state of a crystalline material and its reciprocal space signature, far-field HEDM has become the most common method for most in situ loading experiments. Figure 7 depicts an example of plasticity-induced peak spreading in ff-HEDM data (\( D \approx 1\;{\text{m}} \)) from aluminum alloy, AA1050, specimen loaded in tension to 6 pct strain.[56] Using ff-HEDM, tracking the diffraction peaks from many crystals within a deforming aggregate enables detailed analysis of the crystal rotations associated with plastic deformation being experienced within every crystal. Winther and collaborators examined the average reorientation of each crystal within a deforming aggregate to identify modes of crystallographic slip.[56] These efforts were the first to use ff-HEDM to track crystal reorientation—especially up to the moderate strains necessary to spread plasticity throughout the polycrystal.[56] As depicted in Figure 8, this work provided a direct way to connect to models; predicted lattice reorientations were compared directly to measured values.[57] Plasticity models such as lower bound,[58] upper bound,[59] self-consistent,[60] ALAMEL[61], and finite element models for metals such as aluminum,[57] interstitial free steel[62], and austenitic stainless steel[63] were assessed.

Reprinted from [57] with permission (Color figure online)
(Left) Stereographic triangle showing the rotation of the tensile direction relative to AA1050 crystal orientations as lines. The symbols mark the final orientation of the tensile direction. The triangle is divided into regions (labelled 1 to 4 and with different colors) denoting different rotation behaviors. (Right) Comparison with what the Sachs model (black lines) would predict for each orientation. The inset indicates whether acceptable agreement is found within each region.
4.1.1 Forward Projection Tools
Forward projection is a valuable tool used commonly in many areas of X-ray science. The virtual diffractometer is an example of forward projection used specifically to understand the evolution of polycrystalline metals. Micromechanical model development has been one of the primary drivers for HEXD, in general.[15] The virtual diffractometer provides an alternative to inverting ff-HEDM data to compare to a model. Figure 9 depicts a schematic of the implementation of the virtual diffractometer within a polycrystal plasticity finite element simulation of a tensile test on OMC copper.[64] The conditions of the actual scattering experiment are replicated in the simulation and the center of mass (COM) and the full-width at half-maximum (FWHM) of diffracted intensity peaks in the \(\eta \) (azimuthal) and 2\(\theta \) (radial) directions can be compared directly between the experiment and model for every diffraction peak within every crystal. Spreading in the radial direction is consistent with a lattice strain (stress) gradient. In the end, the goal is to link the spread in the ff-HEDM diffraction data measured on the detector to the plasticity-induced heterogeneous distributions of lattice orientation and stress within the sample—through a model. Even though that spatial information cannot be extracted directly from the ff-HEDM data, this information is contained within the finite element representation. This is shown in Figure 10. Here, the stress and misorientation distributions predicted by the finite element model of an OMC copper crystal, which represents one of the orientations measured in the in situ ff-HEDM loading experiment, are depicted. The measured and simulated COM and FWHM in both \(\eta \) and 2\(\theta \) directions were compared to understand model performance during monotonic tension[64] and fully reversed cyclic loading of the OMC copper.[65] In the cyclic experiment, a bias in the tension–compression asymmetry of the azimuthal FWHM was seen to change when the initial loading changed from tension to compression.[65] Peak spreading (FWHM) in both the radial and azimuthal directions was actually seen to decrease during some load reversals. The somewhat non-intuitive interpretation of peak contraction is that the orientation and strain distributions within a crystal are moving back towards what they were at initial yielding.[65] Cycle-by-cycle evolution of the stress, orientation, and plastic strain rate heterogeneity was also seen in the simulation as was similar contraction of the diffraction peaks.[66] In the end, a favorable comparison of the simulated and experimental data builds confidence that the simulated stress and misorientation distributions are reasonable approximations to those experienced by an actual crystal.

Reprinted from [64] with permission
(Left) Reference element containing a grid of 84 “diffraction centers”. (Right) Simulated diffraction occurring at each diffraction center with the diffracted intensity being projected onto the virtual detector.

Reprinted from [64] with permission
Simulated stress and misorientation distribution for one crystal within an OMC copper aggregate loaded in situ to a uniaxial stress level beyond yielding.
A typical ff-HEDM \(\omega \) scan will capture 50 to 100 diffraction peaks for each crystal. It is often more useful to extract the orientation information from those peaks than use quantities like COM or FWHM directly. To determine the distribution of orientations within a crystal, the spreading of all diffraction peak data can be transformed onto a set of single crystal pole figures and those pole figures can be “inverted” to produce a single grain orientation distribution function (SGODF) cf.[67,68] Another method is to employ the virtual diffractometer to project each point in orientation space onto the virtual detector and choose the lattice orientations that match the peak spreading seen on the actual detector pixel-by-pixel. The bounding area in orientation space—termed the grain orientation envelope (GOE)—that contains all orientations belonging to a single grain can then be determined.[69,70] The SGODF is determined using the intensity information within each crystal.[71]
Nygren et al. conducted continuous loading ff-HEDM experiments on Ti-7Al in uniaxial tension.[69,70] They defined a completeness measure as the difference between the virtual diffractometer projections and diffraction data to decide if a point in orientation space was within the GOE. Figure 11 depicts the evolution of the GOE for one grain within the Ti-7Al sample during the tensile loading, which is also shown. As can be seen, the size, shape and centroidal position of the GOE evolves with straining.[69] Obstalecki et al. defined a “size” of the GOE (they called it \(\bar{\varTheta }\)) and tracked its evolution during fully reversed cyclic loading of a commercially pure copper sample.[72] Reckoning that crystals experiencing larger changes of \(\bar{\varTheta }\) were experiencing the “most” plasticity and might initiate a fatigue crack first, they tracked the evolution of \(\bar{\varTheta }\) for every crystal around the hysteresis loop. They found that the \(\bar{\varTheta }\) distribution changed significantly around the loop during early cycles but seemed to saturate later—similar to the macroscopic stress-strain response of the copper. Crystals that yielded first and plastically deformed the most (greatest change in \(\bar{\varTheta }\)) in early cycles ended the experiment having accumulated “more” plasticity than the other crystals in the aggregate and may become the leading candidates for crack initiation. Finally, to examine the effect of hydrogen on the plasticity experienced by Ni samples deformed in high pressure torsion, Long and Miller used peak intensities to build SGODFs from samples with and without hydrogen.[71] They found that the size (variance) of the distributions were similar, so they computed the kurtosis and skewness tensors from those distributions and compared the norms. Figure 12 shows clusters in a kurtosis norm (\( ||\mathbf {K}|| \)) vs. skewness norm (\( ||{\varvec{\Gamma }}|| \)) plot. The hydrogen-charged samples separated into 2 clusters: a low (\( ||\mathbf {K}|| \)) low (\(||{\varvec{\Gamma }}|| \)) cluster similar to the uncharged sample and a high (\( ||\mathbf {K}|| \)) high (\( ||{\varvec{\Gamma }}|| \)) cluster. This was interpreted as hydrogen changing the nature of the slip or the deformation in the material to be more localized in some crystals but not others.

Reprined from [69] with permission (Color figure online)
Macroscopic Ti-7Al stress-strain curve with the GOE of grain No. 143 plotted for incremental measurements, colored according to their corresponding macroscopic strain. Inset: Cumulative GOE for grain No. 143.

Reprinted from [71] with permission (Color figure online)
Plot of \( ||\mathbf {K}|| \)vs. \(||{\varvec{\Gamma }}||\) for the uncharged grains (green circles), the hydrogen-charged grains assigned to the low cluster (blue triangles), and the hydrogen-charged grains assigned to the high cluster by (red squares).
4.1.2 Twinning and phase transformations
The \(\eta \) and \(\omega \) spreading of the HEDM diffraction peaks—consistent with slip-induced gradients of orientations—can be seen observed in real time on the detector. Since twinning and phase transformations involve the instantaneous orientation shift of a volume of material without gradients, discovery that twinning or a phase transformation has occurred in a polycrystal using ff-HEDM is not as obvious. Methods for understanding twins in a polycrystal—or processes like stress-induced phase transformations—can involve detailed examination of the evolution of orientation pole figures and possibly crystal-by-crystal analysis to understand specific parent–twin relationships.
To study the interplay between slip and twinning, Bieler et al. monitored the evolution of pole figures within a pure Ti sample deformed in uniaxial tension to identify potential twin-parent pairs.[73] Once the twin met a set of configurational criteria including location of its center of mass near the parent grain, the stresses of grains were analyzed. Figure 13 depicts a schematic of a cluster of Ti grains in the aggregate containing several twins. The paper shows that the resolved shear stress criteria—even when using the crystal stresses determined using HEDM—did not account for all twins; indicating twinning could be enhanced by slip from neighboring grains. Abdolvand et al. studied twinning in a larger number of crystals without the parent–twin specificity within a Zircaloy-2 aggregate by reckoning that the increase in the number of indexed crystals as the load increased are due to deformation-induced twins. They used the center-of-mass position, orientation, elastic strain, stress, and the estimated relative grain volume determined from the ff-HEDM experiment to reconstruct the 3D microstructure and statistically study neighborhood effects on the load sharing.[74]
Far-field HEDM has also proven invaluable for understanding stress-induced phase transformations associated with shape memory alloys. Buscek et al. used the virtual diffractometer to verify transformation phases/orientations present in their loaded NiTi sample. Figure 14 depicts the reflections predicted by the virtual diffractometer overlaying the ff-HEDM data.[75] These data enabled important conclusions regarding the applicability of the crystallographic theory of martensite.
(a) The spatial arrangement of grain centroids in the neighborhood of a twin event (10 is the parent grain) in layer 2 of the Ti sample. (b) The same orientations depicted with unit cells showing the parent grain 10 (red unit cell), the twin (purple unit cell) and the neighboring grains in roughly the same relative positions as they appear in (a). Particular slip planes (gray and bronze) are indicated along with their Schmid factors.[73] (Color figure online)

Reprinted from [75] with permission (Color figure online)
The virtual reflections (colored symbols) plotted on top of the experimental diffraction patterns for the identified habit plane variants (HPVs). Sample 1 (a): HPV 10-4 (I-), Sample 2 (b): HPV 9-1 (I-), Sample 3 (c): HPV 3-11 (II-), Sample 3 (d): HPV 3-11 (I+). Two HPV solutions are given for sample 3 because both HPV solutions are present. Data from the first 3 rings are shown. All patterns are summed over the full 360 deg of sample rotation (\(\omega \) in Fig. 1) and take advantage of the fourfold symmetry of the summed diffraction pattern.
4.2 Near-Field HEDM & DCT
Near-field HEDM and DCT both use highly resolved detectors relatively close to the sample. As depicted in Figure 2, these data have high real space resolution and lower reciprocal space resolution. Traditionally, nf-HEDM employed short, line–focused beams. The use of “box beams”—which may result in more spot overlap but can enable more efficient data reduction—was part of the innovation behind DCT. Now box beams are employed in many in situ nf-HEDM experiments. An illustration of the differences between line–focused nf-HEDM (\(\hbox {beam height} = 2\ \mu \hbox {m}\)) and DCT (\(\hbox {beam height} = 350\ \mu \hbox {m}\)) is given in Figure 15, which depicts the diffraction volumes in an Aluminum 0.3 wt pct Mn sample along with a post-mortem EBSD map.[76] The DCT methodology has proven to be quite versatile. Recently a lab-source version of the DCT method for creating grain maps has been implemented employing a polychromatic X-ray beam[77,78]

Reprinted from [76] with permission
Aluminum 0.3 wt pct Mn sample and grain structure imaged with DCT, line-focused HEDM and EBSD. (a) The dog-bone shaped specimen. (b) The positions of the nf-HEDM and EBSD slices within the DCT volume. (c) The DCT volume.
In terms of understanding plasticity processes, capturing spatially resolved subgrain scale lattice reorientation is the great promise of adding in situ loading to both nf-HEDM and DCT. Pokharel et al. studied the deformation of commercially pure copper deformed in tension using nf-HEDM with a \(4\ \mu \hbox {m}\) tall beam.[79] Figure 16 shows one crystal within the deforming copper aggregate colored by two measures of misorientation: intragranular misorientation (IGM)—a long range measure—and kernel average misorientation (KAM)—a short range measure.
DCT-based topotomography is a unique method that allows for simultaneous reconstruction of both the sample microstructure visible in X-ray absorption contrast and the crystallographic grain microstructure as determined from the diffraction signal within a single tomographic scan.[17,18,80] From an instrumentation point of view, topotomography requires additional degrees of positional freedom, since one of the lattice plane normals of the grain has to be aligned parallel to the tomographic rotation axis. A small rocking movement is performed at each rotation position in order to fully illuminate the diffracting grain. Figure 17 depicts the misorientation fields determined using DCT-based topotomography of two adjacent Ti-7Al crystals within a sample deformed to 0.4 pct strain.[81] The authors point out the band-like misorientation structures in the top grain aligned with the (\(01 \bar{1}0\)) slip plane (highlighted in black). Correlation of the misorientation field along the grain boundary seems to indicate interaction of the plastic deformation mechanisms in both grains.

Reprinted from [79] with permission (Color figure online)
One grain within the aggregate colored by IGM (a) and by KAM (b).

Reprinted from [81] with permission
Intragranular misorientation (in degrees) within 2 grains inside a Ti-7Al sample deformed to 0.4 pct strain determined from 6D-reconstruction of topotomographic data.
4.3 Very Far-Field HEDM
Angular resolution on the order of 0.01 can be attained in a vff-HEDM experiment (\( D > 3\;{\text{m}} \)).[19] Using this level of resolution, reciprocal space maps taken at different load levels during stress relaxation in OFHC copper were used to understand intermittent plasticity events associated with the formation and dissolution of subgrains.[20,21] Using machine learning and the Mixed-Mode Pixel Array Detector (MM-PAD), which is capable of capturing high dynamic range images at rates as high as 1 kHz,[82] intermittent plastic deformation was observed in Ti-7Al and AZ31 magnesium.[22] The same experimental configuration at the Advanced Photon Source sector 1, shown in Figure 18, was used to understand localization phenomena in OFHC copper single crystals deformed in compression.[23] The large area detector employed in the far-field experiment has been replaced by a detector “arm” and rotational stage that positions a smaller area detector at the \(\eta \), \(2 \theta \) location of individual diffraction peaks. Note that a far-field detector is placed at \( D \approx 1\;{\text{m}} \) during these vff experiments for simultaneous crystal indexing. The vff setup is an excellent one for the single crystal experiment. However, acquiring information from the number of diffraction peaks necessary for characterizing a polycrystal using the arm and detector setup would be challenging.

Reprinted from [23] with permission
The vff-HEDM experiment setup at APS sector 1. (a) Each diffraction peak is collected individually by positioning the detector. (b) A set of rotation and linear translation stages make up the detector positioning system.
4.4 Multi-detector HEDM
As the number of HEDM users has increased, the use of detectors at multiple distances has become more common. For the box-beam approach to nf-HEDM, it has become quite common to use the orientations from the ff-HEDM data to begin the grain reconstruction process in the undeformed state cf.[47] However, some researchers have used the precision rotation availed by the RAMS2 loadframe at CHESS,[25] which has enabled more seamless transfer of orientation information between the nf and ff detector data, to more thoroughly blend nf and ff data. In their paper studying grain delamination in Al-Li alloys, Tayon et al. colored each crystal in a near-field orientation map according to a combination of the hardening behavior, stress triaxiality, and Schmid factor—all computed using in situ ff-HEDM.[44] Bucsek et al. used RAMS2 and a nf-ff single iteration scheme to determine the evolution of load-induced rearrangements of monoclinic twin microstructures within nickel–titanium specimens containing a few individual crystals.[83] Analyses of the data elucidate the sequence of twin rearrangement mechanisms that occur within localized deformation bands observed on the macroscale using DIC. Nygren et al. used RAMS2 and a data reduction scheme employing multiple iterations between the nf grain map and ff GOE data to reconstruct the orientation fields within all the individual crystals from a Ti-7Al sample deformed to 3 pct strain.[70] A benefit of their new methodology is increased computational efficiency for orientation field reconstruction in comparison with other methods in addition to seamless blending between the two measurement modalities.
5 Discussion
5.1 Nominal In Situ HEDM Experimental Times
In situ HEDM data collection times can vary significantly depending on chemistry, sample thickness, microstructure, X-ray energy, incoming beam flux, detector, and, in the case of nf- and ff-HEDM, the total rotation angle (\(\omega \)). However, general time estimates for measurements can be provided for a typical well-annealed sample with grain diameters on the order of 50 to \(100\ \mu \hbox {m}\) and sample cross sectional dimensions of approximately 1 mm. X-ray energy is usually chosen such that the thickness of the specimen is approximately equal to one attenuation length. The estimates presented here also assume enough vertical scans are performed such that a \(500\ \mu m\) tall region of material is probed. For line-focused nf-HEDM measurements (1 to \(5\ \mu \hbox {m}\) tall beam), each scan takes approximately 1 to 5 minutes depending on the \(\omega \) range. A full volume can be obtained in 8 to 24 hours. For nf-HEDM box-beam measurements (100 to \(250\ \mu \hbox {m}\) tall beam), each scan takes approximately 1 to 3 hours and the time to scan a full volume is approximately 6 to 24 hours. So, depending on the degree of focusing, collecting data for the line scan may not take too much additional time over the box beam. For ff-HEDM box-beam measurements (100 to \(1000\ \mu \hbox {m}\) tall beam), each scan takes approximately 5 to 10 minutes and the time to scan a full volume is approximately 5 to 60 minutes. The total ff-HEDM experimental time for a tension test depends on the number of load steps. Lastly, vff-HEDM measurements consist of individually scanning peaks associated with grains, so the per load step measurement time increases rapidly as more peaks and grains are probed. However, each peak scan can be estimated to take 5 to 20 minutes to collect. The number of peaks scanned is usually chosen such that 1 to 6 hours are spent at each load step.
5.2 Implications for Structure-Based Material Models
Most of the X-ray scattering physics that has enabled the current generation of HEXD methods, in general, and the in situ HEDM methods described in this paper, in particular, were well-established decades ago. It has partially been the availability of the large flux of high-energy X-rays at a third-generation synchrotron and the advancement of area X-ray detectors that have driven the in situ HEDM development. However, the state of metals research, the criticality of the potential applications, and our collective understanding of the important processes around the elastic–plastic behavior of metallic alloys have been the main drivers behind in situ HEDM. The three-dimensional and real time aspects of these high-energy X-ray methods have greatly augmented the informative but limited, mostly forensic, characterization tools of the day. With the ability to track structure and behavior evolution over a volume once referred to as a “material point” (cubic millimeters) with micron (or even submicron) resolution, the impact in situ HEDM is having on material models—from the continuum to atomic scales—could be the most important and long-lasting. Traditionally, plasticity models are built using theories motivated by 2D micrographs and other ex situ characterization experiments such as texture determination—taken either before or after deformation—then are calibrated using mechanical testing data from perhaps multiple experiments on macroscopic test specimens. This is indeed very sparse information for a researcher attempting to use experimental data to motivate, calibrate, and validate a structure-based material model. The data from a “typical” in situ HEDM experiment (like the ones described in this paper) can now contain the orientation and stress state of every crystal within a deforming polycrystalline sample at each point during the experiment when a diffraction experiment is conducted. If we account for the three dimensions of the sample, the three dimensions of orientation space and six-dimensional stress space and time, the HEDM experiment produces is a 13-dimensional dataset. It is an understatement to say that in situ HEDM represents an unprecedented opportunity for the motivation, creation, and validation of physically based material models.
5.3 Spatial and Temporal Resolution and Scope
The ability to delineate diffracted intensity coming from each crystal within a deforming polycrystalline aggregate was what initially enabled in situ HEDM methods; grain maps with one orientation per crystal could be extracted from nf-HEDM experiments and ff-HEDM data could produce grain-resolved orientations and stress tensors. As described in this paper, research groups around the world very quickly started pushing understanding of the distribution of orientations within each crystal and to produce orientation maps (and some stress maps) with intracrystalline resolution. Progress proceeds. With spatial resolution of 30 to 100 nm and angular resolution of 0.001 deg, the dark-field X-ray microscopy instrument at ID06 at the ESRF uses an X-ray objective lens downstream of the sample to produce the most highly resolved orientation and strain maps to date.[84] In terms of time resolution, emerging high-speed detectors like the MM-PAD, which can be optimized using Cd-Te sensors, are enabling image acquisition at rates up to 1 kHz.[82]
5.4 Data Science Challenges and Opportunities
Many of the in situ HEDM advancements that have taken place in last two decades have come about from the opportunities created by larger X-ray fluxes and faster X-ray detectors. The result is an enormous increase in the amount of data acquired during a typical in situ HEDM experiment. Obtaining stress and orientation fields at higher spatial resolution could involve scanning experiments using very small beams over an entire aggregate or, because the best real space resolution is near the sample where the reciprocal space resolution (strains and orientations) is the poorest, the use of multiple detectors positioned at several distances to simultaneously acquire data of varying resolutions in real and reciprocal space. Both of these options increase the volume of data acquired significantly. On the time resolution side, innovations such as the new RAMS loadframe will enable the collection of all data during a in situ ff-HEDM experiment. Dealing with the data flow from these experiments is a challenge on its own—interpreting the data within the context of material behavior is another data science challenge/opportunity. In this paper, we presented results from studies that showed how operating on the raw diffraction data using machine learning methods without any interpretation of the underlying material structure could produce understanding of timing of deformation events and even of the underlying physics of the deformation processes. This trend of using machine learning will persist and expand.
6 Summary/Conclusions
The field of three-dimensional characterization of metallic alloys has truly transitioned from experiments to measurements over the past decade. In situ HEDM is the established leader for 3D measurements in real time during performance and now processing conditions. The overhead for a user of in situ HEDM has been reduced; new high-fidelity, sophisticated load frames, detectors, and data reduction methodologies are in place at high-energy synchrotron light sources around the world. What was an multiyear research effort 5 to 10 years ago is often now a straight-forward measurement. At the same time, new methods such as dark-field X-ray microscopy are enabling measurements with spatial resolution that rivals electron microscopy. There is enormous potential on the computational/data reduction side of in situ HEDM and at the interface with material and scattering models for streamlining the blending of data taken from detectors at multiple distances to enable high resolution in both real space and reciprocal space.
Determining the crystal-averaged stress inside every crystal within a deforming aggregate is a standard ff-HEDM experiment now. These data can provide detailed information about the mechanical complexity within a deforming aggregate and inform stress-based models. Capturing subcrystal spatial resolution of all components of stress—understanding stress gradients—is the frontier in this area. Several approaches are being developed to make that a reality.
-
By scanning a beam much smaller than the average crystal producing ff-HEDM intragrain stress fields can be measured. With existing capabilities, scanning every crystal within an aggregate at every load step of an in situ HEDM experiment will require significant beam time, however.
-
Near-field HEDM methods have subgrain spatial resolution but low strain resolution. For low modulus, high-strength alloys like gum metal, however, including the elastic strains within the DCT data refinement routine has yielded intragrain stresses.
-
Estimates of intragrain gradients of stress and orientation can be obtained by matching the radial spread from ff-HEDM diffraction spots to finite element simulations of the same deforming aggregate.
Stress quantification is an important product of in situ HEDM but is most often done in support of understanding the non-linear behavior of metallic systems—plasticity.
-
Plasticity in the HEDM signal is manifest as (i) smearing or streaking of the peaks in the case of crystallographic slip or (ii) the sudden appearance or disappearance of peaks in the case of twinning or loading-induced phase transformations.
-
Like the crystal-averaged stresses, the evolution of the average orientation of each crystal—which can be obtained using the ff-HEDM signal on its own—has enabled significant crystal plasticity modeling progress. The same can be said for the evolution of the diffracted intensity distributions from the ff-HEDM detector or even the distribution of orientations (SGODF) or the GOEs within the crystals. Those distributions can be compared on a crystal-by-crystal basis to simulations for model validation. Attributes from those distributions have been linked to important plasticity-related processes like hydrogen embrittlement and they can be determined using the ff-HEDM data only—so they can be acquired quickly.
-
Like stress, however, the spatial gradients of lattice orientation within every grain at every possible load step is the important “stand alone” property that should eventually come out of in situ HEDM. For both continuum slip and twinning—especially as they relate to the initiation and propagation of damage and failure, knowing which orientations are present is not enough, we need to know where they are and the morphology. For this reason, the nf-HEDM methods must play a key role.
-
The potential of blending signals from detectors at various distances—perhaps using material models and machine learning—is significant for quantifying intragrain gradients of orientation and stress and, more importantly, what they tell us about intragrain material behavior over every crystal within a deforming aggregate.
References
H. Poulsen, Three-Dimensional X-Ray Diffraction Microscopy, Springer, Heidelberg, U.K., (2004)
M.P. Miller, J.V. Bernier, J.S. Park, A. Kazimirov, Rev. Sci. Instrum., 76, 113903 (2005)
J.V. Bernier, M.P. Miller, J. Appl. Crystallogr., 39, 358-368 (2006)
J.S. Park, P. Revesz, A. Kazimirov, M.P. Miller, Rev. Sci. Instrum., 78, 023910 (2007)
R.M. Suter, C.M. Heffernan, S.F. Li, D. Hennessy, C. Xiao, J. Eng. Mater. Technol., 130, 021007 (2008)
M.P. Miller, J.S. Park, P.R. Dawson, T.S. Han, Acta Metall. Mater., 56, 3927-3939 (2008)
J.V. Bernier, M.P. Miller, J.S. Park, U. Lienert, J. Eng. Mater. Technol., 130, 021021 (2008)
W. Ludwig, P. Reischig, King, M. Herbig, E.M. Lauridsen, G. Johnson, T.J. Marrow, J.Y. Buffière, Rev. Sci. Instrum., 80, 033905 (2009)
J.V. Bernier, J.S. Park, A.L. Pilchak, M.G. Glavicic, M.P. Miller, Metall. Mater. Trans. A, 39, 3120-33 (2008)
U. Lienert, M.C. Brandes, J.V. Bernier, J. Weiss, S.D. Shastri, M.J. Mills, M.P. Miller, Mater. Sci. Eng., A, 524, 46-54 (2009)
J. Oddershede, S. Schmidt, H.F. Poulsen, H.O. Sorensen, J. Wright, W. Reimers, J. Appl. Crystallogr., 43, 539-549 (2010)
U. Lienert, S. Li, C. Hefferan, J. Lind, R. Suter, J. Bernier, N. Barton, M. Brandes, M. Mills, M. Miller, B. Jakobsen, W. Pantleon, JOM, 63, 70-77 (2011)
J.V. Bernier, N.R. Barton, U. Lienert, M.P. Miller, J. Strain Anal. Eng. Des., 46, 527-547 (2011)
J.C. Schuren, S.L. Wong, P.R. Dawson, M.P. Miller, J. Strain Anal., 49, 33-50 (2014)
M.P. Miller, P.R. Dawson, Curr. Opin. Solid State Mater. Sci., 18, 286-99 (2014)
J.C. Schuren, P.A. Shade, J.V. Bernier, S.F. Li, B. Blank, J. Lind, P. Kenesei, U. Lienert, R.M. Suter, T.J. Turner, D.M. Dimiduk, J. Almer, Curr. Opin. Solid State Mater. Sci., 19, 235-44 (2015)
W. Ludwig, P. Cloetens, J. Härtwig, J. Baruchel, B. Hamelin, P. Bastie, J. Appl. Crystallogr., 34, 602-07 (2001)
W. Ludwig, A. King, P. Reischig, M. Herbig, E.M. Lauridsen, S. Schmidt, H. Proudhon, S. Forest, P. Cloetens, S.R. du Roscoat, J.Y. Buffière, T.J. Marrow, H.F. Poulsen, Mater. Sci. Eng., A, 524, 69-76 (2009)
B. Jakobsen, H.F. Poulsen, U. Lienert, W. Pantleon, Acta Mater., 55, 3421-3430 (2007)
B. Jakobsen, H.F. Poulsen, U. Lienert, J. Almer, S.D. Shastri, H.O. Sørensen, C. Gundlach, W. Pantleon, Sci., 312, 889-92 (2006)
B. Jakobsen, U. Lienert, J. Almer, W. Pantleon, H.F. Poulsen, Mater. Sci. Forum, 550, 613-18 (2007)
K. Chatterjee, A.J. Beaudoin, D.C. Pagan, P.A. Shade, H.T. Philipp, M.W. Tate, S.M. Gruner, P. Kenesei, J.S. Park, Struct. Dyn., 6, 014501 (2019)
D.C. Pagan, M. Obstalecki, J.S. Park, M.P. Miller, Acta Mater., 147, 133-148 (2018)
S.R. Ahl, H. Simons, C. Detlefs, D.J. Jensen, H.F. Poulsen, Acta Mater., 185, 142-148 (2020)
P.A. Shade, B. Blank, J.C. Schuren, T.J. Turner, P. Kenesei, K. Goetze, R.M. Suter, J.V. Bernier, S.F. Li, J. Lind, U. Lienert, J. Almer, Rev. Sci. Instrum., 86, 093902 (2015)
N. Gueninchault, H. Proudhon, W. Ludwig, J. Synchrotron Radiat., 23, 1474-1483 (2016)
G.M. Hommer, J.S. Park, Z.D. Brunson, J. Dahal, P. Kenesei, A. Mashayekhi, J.D. Almer, J. Vignes, S.R. Lemmer, B. Clausen, D.W. Brown, A.P. Stebner, Exp. Mech. (Germany), 59, 749-74 (2019)
H. Sharma, R.M. Huizenga, S.E. Offerman, J. Appl. Crystallogr., 45, 705-718 (2012)
H.F. Poulsen, S.F. Nielsen, E.M. Lauridsen, S. Schmidt, R.M. Suter, U. Lienert, L. Margulies, T. Lorentzen, D.J. Jensen, J. Appl. Crystallogr. , 34, 751-6 (2001)
L. Margulies, T. Lorentzen, H.F. Poulsen, T. Leffers, Acta Mater., 50, 1771-79 (2002)
R.V. Martins, L. Margulies, S. Schmidt, H.F. Poulsen, T. Leffers, Mater. Sci. Eng., A, 387, 84-88 (2004)
C. Efstathiou, D.E. Boyce, J.S. Park, U. Lienert, P.R. Dawson, M.P. Miller, Acta Metall. Mater., 58, 5806-19 (2010)
I.G. Dastidar, V. Khademi, T.R. Bieler, A.L. Pilchak, M.A. Crimp, C.J. Boehlert, Mater. Sci. Eng., A, 636, 289-300 (2015)
J. Oddershede, S. Schmidt, H.F. Poulsen, H.O. Sørensen, J. Wright, W. Reimers, J. Appl. Crystallogr., 43, 539-549 (2010)
J. Oddershede, B. Camin, S. Schmidt, L.P. Mikkelsen, H.O. Sørensen, U. Lienert, H.F. Poulsen, W. Reimers, Acta Mater., 60, 3570-3580 (2012)
M. Obstalecki, S.L. Wong, P.R. Dawson, M.P. Miller, Acta Mater., 75, 259-272 (2014)
R. Pokharel, R.A. Lebensohn, D.C. Pagan, T.L. Ickes, B. Clausen, D.W. Brown, C.F. Chen, D.S. Dale, J.V. Bernier, JOM, 72, 48-56 (2020)
G.M. Hommer, J.S. Park, Z.D. Brunson, J. Dahal, P. Kenesei, A. Mashayekhi, J.D. Almer, J. Vignes, S.R. Lemmer, B. Clausen, Exp. Mech., 59, 749-774 (2019)
D. Naragani, M.D. Sangid, P.A. Shade, J.C. Schuren, H. Sharma, J.S. Park, P. Kenesei, J.V. Bernier, T.J. Turner, I. Parr, Acta Mater., 137, 71-84 (2017)
H.M. Paranjape, P.P. Paul, H. Sharma, P. Kenesei, J.S. Park, T.W. Duerig, L.C. Brinson, A.P. Stebner, J. Mech. Phys. Solids, 102, 46-66 (2017)
D.P. Guillen, D.C. Pagan, E.M. Getto, J.P. Wharry, Mater. Sci. Eng., A, 738, 380-388 (2018)
D.C. Pagan, P.A. Shade, N.R. Barton, J.S. Park, P. Kenesei, D.B. Menasche, J.V. Bernier, Acta Mater., 128, 406-417 (2017)
D.C. Pagan, J.V. Bernier, D. Dale, J.Y.P. Ko, T.J. Turner, B. Blank, P.A. Shade, Scr. Mater., 142, 96-100 (2018)
W.A. Tayon, K.E. Nygren, R.E. Crooks, D.C. Pagan, Acta Mater., 173, 231-241 (2019)
D.C. Pagan, J. Kaminsky, W.A. Tayon, K.E. Nygren, A.J. Beaudoin, A.R. Benson, JOM, 71, 3513-3520 (2019)
A.J. Beaudoin, P.A. Shade, J.C. Schuren, T.J. Turner, C. Woodward, J.V. Bernier, S.F. Li, D.M. Dimiduk, P. Kenesei, J.S. Park, Phys. Rev. B, 96, 174116 (2017)
N.Y. Juul, G. Winther, D. Dale, M.K.A. Koker, P. Shade, J. Oddershede, Scr. Mater., 120, 1-4 (2016)
T.J. Turner, P.A. Shade, J.V. Bernier, S.F. Li, J.C. Schuren, P. Kenesei, R.M. Suter, J. Almer, Metall. Mater. Trans. A, 48, 627-47 (2017)
P. Reischig, W. Ludwig, 40th Risoe International Symposium on Metal Microstructures in 2D, 3D and 4D, Risoe, Denmark, (2019). arXiv:hal-02404435
B. Jakobsen, H.F. Poulsen, U. Lienert, J. Bernier, C. Gundlach, W. Pantleon: Phys. Status Solidi A, 206, 21-30 (2009)
D.C. Pagan, A.J. Beaudoin, J. Mech. Phys. Solids, 128, 105-116 (2019)
Y. Hayashi, D. Setoyama, Y. Hirose, T. Yoshida, H. Kimura, Sci., 366, 1492-96 (2019)
N.A. Henningsson, S.A. Hall, J.P. Wright, J. Hektor, J. Appl. Crystallogr. 53, 486–93 (2020)
J.F. Nye, Acta Mater., 1, 153-62 (1953)
A.F. Joffe, M.V. Kirpitcheva, Philos. Mag. Series 6, 43, 204-06 (1922)
H.F. Poulsen, L. Margulies, S. Schmidt, G. Winther, Acta Mater., 51, 3821-30 (2003)
G. Winther, L. Margulies, S. Schmidt, H.F. Poulsen, Acta Mater., 52, 2863-2872 (2004)
G. Sachs, VDIZ, 12, 134-136 (1928)
G.I. Taylor, J. Inst. Met., 62, 307-324 (1938)
B. Clausen, T. Lorentzen, T. Leffers, Acta Mater. (UK), 46, 3087-98 (1998)
L. Delannay, P. Van Houtte, I. Samajdar, J. Phys. IV, 9, Pr9-43-Pr9-52 (1999)
G. Winther, J.P. Wright, S. Schmidt, J. Oddershede, Int. J. Plast., 88, 108-125 (2017)
N.Y. Juul, J. Oddershede, G. Winther, JOM, 72, 83-90 (2020)
S.L. Wong, J.S. Park, M.P. Miller, P.R. Dawson, Comput. Mater. Sci., 77, 456-66 (2013)
M. Obstalecki, S.L. Wong, P.R. Dawson, M.P. Miller, Acta Mater. , 75, 259-272 (2014)
S.L. Wong, M. Obstalecki, M.P. Miller, P.R. Dawson, J. Mech. Phys. Solids, 79, 157-185 (2015)
P.C. Hansen, H.O. Sorensen, Z. Sukosd, H.F. Poulsen, SIAM J. Imaging Sci. (USA), 2, 593-613 (2009)
N.R. Barton, J.V. Bernier, J. Appl. Crystallogr., 45, 1145-1155 (2012)
K.E. Nygren, D.C. Pagan, M.P. Miller, IOP Conf. Ser.: Mater. Sci. Eng., 580, 012018 (2019)
K. Nygren, D. Pagan, J. Bernier, M. Miller: Mater. Charact., 2020, vol. 165, p. 110366
T.J.H. Long, M.P. Miller, Integr. Mater. Manuf. Innov., 8, 423-439 (2019)
M. Miller, C. Budrow, T. Long, M. Obstalecki, IOP Conf. Ser.: Mater. Sci. Eng., 580, 012009 (2019)
T.R. Bieler, L. Wang, A.J. Beaudoin, P. Kenesei, U. Lienert, Metall. Mater. Trans. A, 45A, 109-122 (2014)
H. Abdolvand, M. Majkut, J. Oddershede, J.P. Wright, M.R. Daymond, Acta Mater., 93, 246-55 (2015)
A.N. Bucsek, D. Dale, J.Y.P. Ko, Y. Chumlyakov, A.P. Stebner, Acta Crystallogr. Sect. A, 74, 425-446 (2018)
L. Renversade, R. Quey, W. Ludwig, D. Menasche, S. Maddali, R.M. Suter, A. Borbély, IUCrJ, 3, 32-42 (2016)
A. King, P. Reischig, J. Adrien, S. Peetermans, W. Ludwig, Mater. Charact., 97, 1-10 (2014)
F. Bachmann, H. Bale, N. Gueninchault, C. Holzner, E.M. Lauridsen, J. Appl. Crystallogr., 52, 643-651 (2019)
R. Pokharel, J. Lind, S.F. Li, P. Kenesei, R.A. Lebensohn, R.M. Suter, A.D. Rollett, Int. J. Plast., 67, 217-234 (2015)
H. Proudhon, N. Gueninchault, S. Forest, W. Ludwig: Materials (2018). https://doi.org/10.3390/ma11102018
W. Ludwig, N. Vigano, H. Proudhon, 40th Risø International Symposium : Metal Microstructures in 2D, 3D and 4D, Risoe, Denmark, (2019). arXiv:hal-02404426
M.W. Tate, D. Chamberlain, K.S. Green, H.T. Philipp, P. Purohit, C. Strohman, S.M. Gruner, J. Phys.: Conf. Series, 425, 062004 (2013)
A.N. Bucsek, D.C. Pagan, L. Casalena, Y. Chumlyakov, M.J. Mills, A.P. Stebner, J. Mech. Phys. Solids, 124, 897-928 (2019)
M. Kutsal, P. Bernard, G. Berruyer, P.K. Cook, R. Hino, A.C. Jakobsen, W. Ludwig, J. Ormstrup, T. Roth, H. Simons, K. Smets, J.X. Sierra, J. Wade, P. Wattecamps, C. Yildirim, H.F. Poulsen, C. Detlefs, IOP Conf. Ser.: Mater. Sci. Eng., 580, 012007 (2019)
Acknowledgments
The science described in this paper was supported by funding agencies around the world and is acknowledged in the original manuscripts. Acknowledgment of the synchrotron facilities here is appropriate, however: the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357, the Cornell High Energy Synchrotron Source (CHESS), and the Center for High Energy X-ray Sciences (CHEXS), which is supported by the National Science Foundation under Award DMR-1829070, the European Synchrotron Radiation Facility (ESRF), and the Super Photon ring-8 GeV (SPring-8) with the approval of the Japan Synchrotron Radiation Research Institute (JASRI).
Conflict of interest
The authors declare that they have no conflicts of interest.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Manuscript submitted March 9, 2020.
Rights and permissions
About this article
Cite this article
Miller, M.P., Pagan, D.C., Beaudoin, A.J. et al. Understanding Micromechanical Material Behavior Using Synchrotron X-rays and In Situ Loading. Metall Mater Trans A 51, 4360–4376 (2020). https://doi.org/10.1007/s11661-020-05888-w
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-020-05888-w