Abstract
Settling of solid particles in a stratified ambient fluid is a process widely encountered in geophysical flows. A set of experiments demonstrating the settling behaviour (the pattern of trajectory, variation of particle orientation, and settling velocity with depth) of thin disks descending through a nonlinear density transition was performed. The results showed complex hydrodynamic interactions between a particle and a liquid causing settling orientation instabilities and unsteady particle descent in low to moderate Reynolds number regime. Five phases of settling were observed: two phases with stable horizontal, one with stable vertical disk position, and two reorientation phases; moreover, two local minima of settling velocity were identified. It was demonstrated that thresholds for local minima and the first reorientation depend on the settling dynamics in an upper layer, stratification conditions, and disk geometry. The comparison of settling behaviour of thin disks varying in diameter revealed that settling dynamics is sensitive to particle geometry mainly in the upper part of density transition with a non-obvious result that the first minimum velocity is smaller for a disk with a larger diameter than for a disk with a smaller diameter. The analysis of settling trajectory showed that two reorientations are accompanied with a horizontal drift, which may be important in the context of interactions between particles settling in a group.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Density stratification occurs in various fluid components of natural environment (ocean, atmosphere, and the Earth’s interior) and affects to a large extent the vertical transport of particles. Modification of settling or rising behaviour of rigid particles, drops, and bubbles due to the presence of sharp or continuous stratification may considerably influence geophysical processes.
Density gradients form in aquatic systems (ocean, seas, and lakes) as a consequence of temperature and/or salinity variation with depth. The settling dynamics of particles in a density-stratified ambient is much different from that in homogeneous conditions. Sharp density gradients known as pycnoclines (haloclines or thermoclines, with salinity or temperature acting as a stratifying agent, respectively) form in favourable conditions (Capet et al. 2016; Noufal et al. 2017) induced the deceleration and prolonged residence times of particles in the stratified region (Peperzak et al. 2003). Field observations have provided evidence that organic particles such as marine, lake snow, and faecal pellets may stagnate at pycnoclines for a few days, forming the so-called thin layers (Diercks et al. 2019; Macintyre et al. 1995; Prairie et al. 2015), which modify particulate organic carbon flux in the ocean (Arnosti 2011; Lutz et al. 2002; Prairie et al. 2017).
Atmosphere stratification affects the transport dynamics of various particles including dust, aerosol, pollens, volcanic ashes, and pollutants. Temperature inversion layer that may form in the troposphere prevents airborne particles from settling, which has been observed for dust (Zhai et al. 2019). Moreover, the stratification of atmosphere affects the fate of eruption columns and the transport of volcanic particles including settling of ashes (Woods 1995). In the context of Earth’s interior, it has been demonstrated that the presence of sinking crystals may considerably accelerate mixing between rhyolitic and basaltic magmas, suggesting that particle settling should be considered in the magma mixing process (Renggli et al. 2016).
The effects of fluid stratification on the movement of an object are also important in oceanographic techniques allowing to measure physical, e.g. temperature and salinity, as well as biological parameters across the ocean depth. The design and operation of oceanographic float take advantage of natural density stratification, since the device actively changes its depth by manipulating its density with reference to ambient conditions to achieve the equilibrium depth. Although the dimensions of floats considerably exceed the above-mentioned natural particles, the same physical processes govern the settling and rising of objects in stratified fluid (D'Asaro 2018).
Research on the dynamics of particle settling in stratified conditions is still at the level of fundamental mechanics of particle motion, since density gradient effects considerably increase the complexity of the problem compared to the homogeneous conditions. While settling in a homogeneous fluid is conveniently characterised by Reynolds number, Re = U a/ν, where U is the settling velocity [m s−1], a—particle characteristic length [m], ν—kinematic viscosity [m2 s−1], when stratified fluid is considered, stratification effects are usually accounted by stratification strength expressed as the Brunt–Vaisala buoyancy frequency N, and Froude number, Fr = U/N a, which is the ratio of inertial to buoyancy forces (Yick et al. 2009). Another parameter is the ratio between momentum diffusivity and mass diffusivity of stratifying agent, i.e. Schmidt number, Sc = ν/κ where κ is the diffusivity of stratifying agent [m2 s−1] (or Prandtl number for temperature).
Since detailed research on individual particle dynamics is challenging in natural conditions, small-scale laboratory experiments and numerical studies have become the major means to extend our knowledge on the fundamental aspects of sedimentation process (Prairie and White 2017). Earlier studies considered linear ambient stratification (Doostmohammadi et al. 2014; Mercier et al. 2020; Yick et al. 2009), a two-layered configuration with a sharp density transition (Abaid et al. 2004; Camassa et al. 2010; Srdic-Mitrovic et al. 1999; Verso et al. 2019), and a two-layered configuration with a continuous nonlinear transition (Mrokowska 2018). Previous experimental studies have referred to the sedimentation in stratified conditions in a general sense, however, with a strong focus on natural waters where stratification is generated by the vertical variation of salinity and temperature.
Density of particles present in aquatic systems (detrital material, mineral particles, plankton, microplastics, and marine snow) is close to that of water, which in combination with small dimensions of particles makes them settle in a low and moderate Reynolds number regime. Viscous forces dominate for Re ≪ 1, while inertial forces affect the settling dynamics for Re higher than unity. A group of studies motivated by settling processes in marine systems focused on settling in the viscous regime (Camassa et al. 2010; Yick et al. 2009), while others considered low to moderate Re number inertia-controlled regimes (Kindler et al. 2010; Mrokowska 2018; Prairie et al. 2015).
It has been well acknowledged in research performed so far that pronounced deceleration of particles at pycnoclines observed in nature is due to stratification-induced drag, which appears in the presence of density gradient beside the drag characteristic for homogeneous conditions (Magnaudet and Mercier 2020; Srdic-Mitrovic et al. 1999). The origin of stratification-induced drag is attributed to a caudal fluid entrained in the wake of particle from the above layers of lighter fluid (Srdic-Mitrovic et al. 1999) and to the compression and distortion of isopycnals (Doostmohammadi et al. 2012; Yick et al. 2009). These two basic mechanisms have been demonstrated for spheres using both laboratory experiments and numerical simulations. Inertial waves generated by descending particle may be the source of additional drag (Srdic-Mitrovic et al. 1999; Yick et al. 2009); however, this applies only for moderate and high Re number regimes in which case the particle has large inertia (Okino et al. 2017; Scase and Dalziel 2004).
Although the knowledge on the mechanisms of particle deceleration in the presence of stratification is growing, it is still not sufficient to propose robust methods that could be applied in sedimentation studies by a wide community of earth and environmental sciences researchers. Existing sedimentation and biogeochemical models oversimplify ambient conditions due to insufficient existing knowledge on how to tackle complex physical properties of natural waters in combination with settling processes, which may cause misestimating of sedimentation fluxes (Lutz et al. 2002). Effects of stratification are either discarded or limited to the effect of density change with the assumption that formulas for homogeneous conditions hold in stratified ambient, while settling velocity is much lower in a stratified background configuration than predicted by the standard Stokes law formula (Dey et al. 2019) for the corresponding homogeneous conditions due to stratification-induced drag (Camassa et al. 2009), which has serious implications on the estimation of particulate flux. Despite some successful attempts to parametrize the sedimentation through a pycnocline (Prairie and White 2017), research on sedimentation in stratified conditions has not yet provided robust methods to be applied easily in large-scale or local-scale models.
Another troublesome factor affecting settling process is the shape of a particle. The vast majority of particles present in natural fluid systems are non-spherical; some examples are irregular volcanic ashes (Saxby et al. 2018), aeolian sediments (Raffaele et al. 2020), microplastics (Cole et al. 2011), faecal pellets, microorganisms, and marine snow (Turner 2015). Basic research within fluid mechanics and sedimentology provides some theoretical bases for the estimation of settling velocities (Dietrich 1982; Loth 2008); however, existing theoretical background for the assessment of settling dynamics of solid particles of various shapes and densities is not sufficient to effectively study geophysical and environmental problems such as settling speeds and fluxes of marine snow (Laurenceau-Cornec et al. 2019), microplastics in the ocean (Khatmullina and Isachenko 2017), and particulate organic matter flux (Lutz et al. 2002). The major problem is the fact that settling dynamics of variously shaped particles cannot be described by a universal law, as in the case of a sphere, and attempts to apply formulae dedicated for a sphere results in unreliable settling velocity estimations (Saxby et al. 2018). Consequently, an excessive number of semi-empirical relations to calculate drag coefficient and settling velocity have been derived. However, these relations have serious limitations on their applicability due to shape-dependent and orientation-dependent drag (Bagheri and Bonadonna 2016; Loth 2008). These practical problems have been already faced in research on settling fluxes of microplastics (Khatmullina and Isachenko 2017; Waldschlager and Schuttrumpf 2019) and biogenic particles (Maggi 2013).
Since our state of knowledge is not sufficient to properly account for stratification effects in sedimentation models, fundamental studies on settling dynamics of non-spherical particles in stratified ambient are necessary to formulate in the future effective methods that will be applied in models. A few basic studies performed so far demonstrated that shape effects have pronounced impact on particle settling dynamics in stratified systems (Doostmohammadi and Ardekani 2014; Mercier et al. 2020; Mrokowska 2018). Spheroid particles reorient at a density interface as the effect of buoyancy-induced torque appearing due to pressure difference at the edges of particle which overcomes inertial torque, which leads to complex pattern of settling behaviour (Ardekani et al. 2017; Doostmohammadi and Ardekani 2014; Mrokowska 2018). Disk rotation has been claimed to be additionally amplified by the torque exerted by a jet moving from the centre of the disk to its edge (Mercier et al. 2020), an effect visualized also in Mrokowska (2018).
Disk-like particles constitute a large group of particles that are of significance in environmental processes, e.g. diatoms, minerals, and ashes, and are convenient representation of oblate spheroids. Therefore, their dynamics are worth studying in the context of sedimentation in natural fluid systems. The pattern of individual disk settling has been described for two ambient conditions so far: a linear (Mercier et al. 2020) and nonlinear stratification (Mrokowska 2018). In the first study, short-length cylinders settling in a linearly stratified liquid have been considered (Mercier et al. 2020), and in the second one thin disks settling though a density transition have been studied (Mrokowska 2018). In the linear stratification set-up, the whole water column has been stratified with the maximum density exceeding the density of a particle, while in the other case there has been a two-layered set-up with two homogeneous layers of liquid: a less dense upper and a denser lower, both of density smaller than the density of the particle, with a nonlinear density transition between the layers. For both configurations, a disk reorients from stable horizontal to stable vertical position after some distance fallen broadside on in a stratified layer, which has been described as phase 1 and 2 in Mercier et al. (2020) and phases 1, 2, 3 in Mrokowska (2018). However, the dynamics of a disk settling in a nonlinear stratification are more complex, which manifests in two local velocity minima, while no minima have been observed for linear stratification. It should be noted that the first velocity minimum is an effect of particle deceleration during reorientation and the second one is achieved when a disk is in vertical position, but occurs only when stratification is sufficiently strong (Mrokowska 2018). Two different mechanisms have been described for the reorientation from vertical to horizontal position. In the case of a linear stratification, reorientation occurs when the particle achieves the level of neutral buoyancy, which is described as phase 3 in (Mercier et al. 2020), while in the nonlinear stratification the second reorientation is an effect of fading influence of stratification when the particle enters the lower homogeneous layer where the role of inertia is restored. This is described as phase 4, and further settling in a stable horizontal position in the lower layer is denoted as phase 5 (Mrokowska 2018).
Another study (Lam et al. 2019) has investigated the settling of heavy disks in a stably stratified liquid column for Re of order 1000. In this study, the effect of stratification on secondary motion of disk, specifically a fluttering mode, has been examined. The study showed that, compared to a homogeneous fluid, stratification modifies settling dynamics enhancing particle radial dispersion, decreasing settling velocity, inclination angle, and uttering amplitude.
The settling process through stratified fluid has not been yet well recognised at the fundamental level, and deeper insight into settling dynamics of non-spherical particles in a stratified fluid is necessary to enable development of methods that will improve the performance of sedimentation estimations and particle flux modelling in future. This study aims at improving our understanding of non-spherical particles settling in stratified conditions. I show a series of settling experiments in a two-layered water column with nonlinear density transition extending the previous research (Mrokowska 2018) to focus on new aspects of settling dynamics. To gain more detailed characteristics of disk settling behaviour in a transition layer, 3D trajectory of particle settling was retrieved. The settling dynamics of thin disks were evaluated for a range of settling conditions in an upper layer and various stratification strengths in a density transition region. Two types of thin disks varying in diameter were used in this study. The objectives of the study was to (1) quantify the effect of settling conditions in an upper layer and stratification characteristics on the settling behaviour, i.e. settling velocity, reorientation pattern, and particle trajectory of disks in a low and moderate Re number regime, and to (2) assess the effect of disk diameter on settling dynamics.
Methods
Characterization of particles and experimental set-up
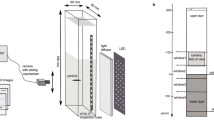
Experiments were carried out in the Laboratory of Hydrodynamic Micromodels, Institute of Geophysics, Polish Academy of Sciences, Warsaw, Poland. Disks were manufactured from acrylonitrile butadiene styrene (ABS) foil with a density of 1050 ± 5 kg m−3 and thickness h = 50 μm. Specially designed puncher was used to produce two sets of disks differing in diameter, d—2 mm and 3 mm with 0.1 mm accuracy, denoted as d2 and d3 disks, respectively. Disks were considered thin with a geometrical aspect ratio χ = d/h equal to 40 and 60. Several disks of each type were prepared, and diameters were verified by image analysis using one of cameras applied in this study to take high-resolution photographs.
Disk settling was investigated in a series of experiments carried out in a 0.50-m-high transparent tank with a square base (0.10 × 0.10 m). A two-layered water column was formed before an experiment by filling the tank with denser salt water solution (density ρll) up to about 0.19 m from the bottom and with less dense salt water solution (density ρul) from 0.19 m up to the height of about 0.48 m. Thereby, two layers referred to as an upper and lower layer were formed (Fig. 1). To fill the tank, a method applied in the previous study has been used where details are described (Mrokowska 2018).
To estimate vertical variation of salinity, a procedure described in the mentioned paper was applied. Inspection holes spaced every 5 mm (Fig. 1) were used to sample aqueous salt solution, and the salinity of each sample was measured using Kruss refractometer, model DR301-95. Given the temperature measurements, salinity was recalculated to density using literature tables (Kestin et al. 1981). The vertical variation of density was fitted to the hyperbolic tangent function (Prairie et al. 2015), as in previous study (Mrokowska 2018). The experiments were carried out at room temperature varying in a range 22.1–23.4 °C.
A particle was released beneath a water surface in the centre of x–y plane, and particle descent in density transition region was recorded using two identical cameras (Basler acA2500-60um equipped with Schneider–Kreuznach macro lenses Componon 2.8/28–001) positioned orthogonal to each other. Camera#1 filmed x–z plane and camera#2 y–z plane (Fig. 1), which enabled the reconstruction of particle trajectory. Two LED panels with DC power supply were used to generate backlight necessary to visualise the settling particle and to record the projection of particle shadow. The field of view (FOV) of a camera covered 77-mm-high and 62-mm-wide area with one pixel corresponding to 31 μm. Upper edges of both cameras FOV were precisely positioned to the same level slightly above the density interface. Particle trajectories were recorded at 60 fps, and the capturing of image pairs was synchronized. Each settling test was repeated a few times.
The settling of a few disks of the same type was investigated in each experiment to check the repeatability of an experiment. The number of repetitions varied from 2 to 5 and was constrained by (1) the quality of visualisation in two orthogonal planes (tests were discarded from analysis when a particle was settling not in the centreline of the tank) and (2) timescale of mixing in transition layer due to diffusion and mixing induced by settling particles.
Experimental set-ups were checked for the optical distortions, due to possible change of refractive index in density-stratified fluid, using a ruler (Abaid et al. 2004) and examining the dimensions of settling particles in experimental images; no deformations have been observed.
Cameras location enabled recording particle settling only in the transition layer; hence, another set of experiments in homogeneous conditions corresponding to settling conditions in an upper layer were performed in the same tank to assess terminal settling velocity in the upper layer. In these experiments, only one camera was used to record settling particle in FOV positioned about 0.3 m below a free water surface to ensure terminal settling conditions.
Processing of images
Pairs of orthogonal views of settling disk (images captured by camera#1 and camera#2) were obtained from each experimental test on particle settling within density transition. Image analysis was performed using procedures available in ImageJ and using ad hoc scripts in MATLAB® following methods applied in the previous studies (Mrokowska 2018; Mrokowska and Krztoń-Maziopa 2019) to identify particles and assess their position. Thresholding method was applied to assess the contours of particle projection in each image. Coordinates of particle projection geometrical centre representing the centre of mass were evaluated from image pairs, which were next used to retrieve the particle trajectory. Small vertical shifts (not exceeding 1.1 mm in average) between images in each pair were corrected based on the location of the first minimum velocity (defined further in the test), which is unequivocal in both images. Time-resolved position data were smoothed by a moving-average cubic polynomial using Savitzky–Golay filter. Settling velocity was evaluated as a central-point difference quotient using particle position data and time step between consecutive images (Mrokowska 2018; Mrokowska and Krztoń-Maziopa 2019).
Experimental conditions
Three sets of experiments in a two-layered configuration were carried out with density of upper layer, ρul, ranging between 1003 and 1016 kg m−3, while the density of lower layer was constant (ρll = 1036 kg m−3). Viscosity of fluid was assumed constant for the purposes of data analysis, since the difference in viscosity between an upper and lower layer was insignificant (smaller than 5%). Names of experiments ES%dx reflect salinity in an upper layer and a disk diameter, where S stands for salinity [%] and x is a diameter [mm]. Details on the physical properties of liquids are reported in Table 1.
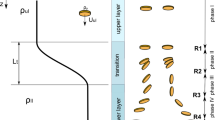
Density of ambient fluid varies nonlinearly with depth. Figure 2 shows vertical distribution of ambient fluid density, ρf, both measured and fitted to the hyperbolic tangent function (Eq. 1) with R2 > 0.99:
where ρf is the density of fluid [kg m−3], ρul and ρll—density of homogeneous upper and lower layer, respectively [kg m−3], z—vertical coordinate [m], z0, p—fitting parameters [m]. Density jump, b = (ρll—ρul)/ρul, indicating density difference between an upper and lower layer varies between 0.020 and 0.033. Brunt–Vaisala buoyancy frequency, N, varies within density transition (increases with rising density gradient (Fig. 2)) and was evaluated from the formula:
where g = 9.81—acceleration due to gravity [m s−2], \(\frac{{\partial \rho_{f} \left( z \right)}}{\partial z}{ }\)—background density gradient. Since there is no specific value of N as in the linear stratification, the maximum buoyancy frequency Nmax is defined to be a general parameter describing stratification strength for the purposes of this study. Buoyancy frequency increases with density jump with Nmax varying from 4.328 to 5.980 (Table 1).
Transition thickness, Lt, does not vary significantly between the three experiments; however, it decreases slightly with the increasing density jump. Transition thickness relative to disk diameter, Lt/d, varies from 12 to 20 (Table 1) and is considered continuous, since it exceeds the dimensions of particles in contrast to sharp interface configurations where the thickness of density transition was comparable with particle dimensions (Blanchette and Shapiro 2012; Camassa et al. 2009).
Experiments in homogeneous conditions referring to terminal settling in an upper layer accompanied each two-layered experiment. Two homogeneous experiments, each comprising several repetitions, were performed for each configuration to gather meaningful number of repetitions, and the experimental conditions are reported in Table 2. These data were used to analyse the impact of settling parameters in an upper layer on particle settling behaviour within the transition layer. Reynolds number in an upper layer (or entrance Reynolds number) is defined as Reul = d Uul/ν, where Uul denotes the terminal settling velocity (Table 2).
This study has been a continuation of previous experimental research (Mrokowska 2018) extending the range of conditions and focusing on the quantification of the effects of density transition on settling behaviour of disks. In the present study, stratification strength was controlled by the density of upper layer varying between three experiments, while the density of lower layer was kept constant. Conversely, the density of upper layer was kept constant in the previous study. Here, the thickness of transition layer, Lt, was almost constant (0.037–0.040 m) in all experiments. Hence, density jump between upper and lower layer may be considered as the main source of stratification variability within transition layer with negligible impact of transition thickness. This is different configuration than studied in the previous research, where the stratification strength was controlled by the transition thickness. Disks used in the present study were of larger diameter than in the previous one where diameters smaller than 2 mm were investigated.
Since fluid density, buoyancy frequency, and settling velocity are variable with depth for a particle translating in a nonlinear stratification, it is sensible to consider parameters as a function of depth. In such conditions, Reynolds number reads:
Archimedes number for a disk with characteristic length taken as equivalent sphere diameter (sphere of the same volume) is (Auguste et al. 2013):
where ρp is the particle density [kg m−3].
Froude number within transition layer reads:
A ratio between Reynolds and Froude number forms another useful parameter (Mercier et al. 2020):
Settling velocity was estimated using a standard approach in homogeneous fluids to demonstrate to what extent oversimplified approach using formulas dedicated to homogeneous conditions may misestimate particle settling velocity and residence times in density transition. Settling velocity was evaluated iteratively using the equation for steady settling velocity of a disk:
with drag coefficient, Cd, calculated from the formula dedicated to a terminal falling of a disk with Re number between 1.5 and 133 (Clift et al. 1978):
Results and discussion
Phases of disk settling and evolution of settling velocity
Disk settling dynamics followed the pattern observed in the previous research (Mrokowska 2018) where five phases of settling were identified (please refer to the explanation therein). Figure 3 presents the typical variation of settling velocity with depth, where characteristic velocities, i.e. the first local velocity minimum, umin1, the second local velocity minimum, umin2, and mean locations for the beginning of phase II and III with corresponding standard deviations, are shown.
Evolution of instantaneous settling velocity with depth for two-layered experiments (a) E2.6%d2, (b) E1.6%d2, (c) E0.7%d2, (d) E2.6%d3, (e) E1.6%d3, (f) E0.7%d3 with the location of characteristic velocities umin1, umin2. Vertical location of the onset of phases—the beginning of phase II (ph II) and the beginning of phase III (ph III) are mean locations for all experimental runs accompanied with standard deviation shown as a grey area. Settling velocity is non-dimensionalized by the terminal settling velocity in an upper layer, Uul, and particle position by a disk diameter, d. (z − z0)/d = 0 corresponds to the upper boundary of transition region
Disks were settling in an upper homogeneous layer (phase I) with terminal velocity varying from 0.0025 to 0.0032 m s−1 for d2 disks and from 0.0030 to 0.0037 m s−1 for d3 disks (not shown in the figure). Disks were translating broadside on, which is in line with phase diagrams describing dynamics of disks in terms of the relation between Re and dimensionless moment of inertia, I* (Field et al. 1997; Willmarth et al. 1964) with the range of parameters observed in the study, Re between 5.0 and 11.1, and I* of the order 1 × 10–3, corresponding to the steady falling mode. Disks entered the transition with a broadside position and continued to settle in this orientation experiencing deceleration due to stratification effects.
Figure 3 shows that the location of the first minimum velocity, umin1, corresponds with the beginning of reorientation (beginning of phase II). A particle assumes vertical position around the level where N = Nmax, which may indicate that the maximum density gradient enhances rotation of particle to the vertical position. After the reorientation, the particle continues settling in a stable vertical position with a broadside perpendicular to horizontal (phase III) until stratification effects dominate over the inertia. It has been confirmed numerically in other study (Mercier et al. 2020) that stratification supports the descent of disk in a vertical position when settling velocity is low enough. Vertical position seems to be quite stable, and some particles descended in this position much further than others reaching the onset of reorientation to the horizontal position outside the camera field of view. It suggests that the orientation instability may be triggered not only by the stratification conditions but may be also induced by imperfections on the particle surface or in the location of the centre of mass, which may modify pressure distribution around the particle inducing rotation. Thus, “imperfect disks” are likely to change orientation earlier than perfect ones. The reorientation to the horizontal position occurs in a gliding motion with fading stratification effects when a disk is leaving the transition (phase IV). All studied disks achieved the second minimum velocity, umin2, when translating in vertical position, which is analysed further in this paper.
Since phase IV (reorientation from vertical to horizontal position) was not recorded for some data sets due to limited field of view, data analysis for this phase is only partial. All particles assumed a stable horizontal position in a lower homogenous layer (phase V); however, this phase was outside FOV and has not been presented herein.
Data presented in Fig. 3 indicate that repeated experimental tests show a good agreement up to the point when particles achieve the level of maximum buoyancy frequency. This agreement is in both settling velocity values and the location of reorientations. Below this level, the dispersion of settling velocity is observed and the onset of reorientation from vertical to horizontal position does not have a unique location.
All disks travelled some vertical distance in density transition before they started to reorient from a stable horizontal to vertical position. (See the location of the beginning of phase II in Fig. 3.) Similar effect has been observed in a linear stratification where it was found that stable broadside on position changes to vertical when a disk decelerates to some threshold velocity (Mercier et al. 2020). However, when we compare the settling velocity profile in a linear and nonlinear stratification, significant differences are evident. First of all, in a linear stratification velocity decreases monotonically (Mercier et al. 2020). Conversely, in the case of a nonlinear density gradient, a particle decelerates and accelerates in response to the variable stratification strength, which is additionally combined with the change of particle orientation. Consequently, drag exerted on a particle is a combination of buoyancy variation due to vertical density gradient, stratification strength, and axisymmetric particle shape. Quantification of drag is still challenging in such conditions and needs consideration in future studies.
Effect of stratification on evaluation of settling velocity and residence time
Figure 4 presents the sample results of setting velocity estimation using Eq. (7) with drag coefficient defined with Eq. (8), the approach which is relevant in homogeneous conditions. The results are presented here to demonstrate that methods derived for a homogeneous fluid may result in serious misestimating of settling process in the presence of stratification. This approach showed satisfactory results in an upper homogeneous layer, slightly underestimating settling velocity with percentage error 100(ucal − uobs)/uobs, where ucal is the settling velocity calculated with Eq. (7) and uosb is a measured value, between 4 and 10%. However, the comparison of the results obtained with Eq. (7) with velocities measured in the density-stratified region reveals significant deviations between estimated and observed values, which is shown in Fig. 4. First of all, this approach does not reproduce the existence of settling velocity minima. Consequently, predicted settling velocity in the major part of transition layer is larger than observed values. Secondly, this approach underestimates residence time of a particle in the transition layer (A–B in Fig. 4) as well as in the region where the particle was tracked (A–C region in Fig. 4). Results presented in Table 3 show that measured residence times in the transition are up to threefold larger than estimated by the homogeneous fluid approach. Moreover, the formula underestimates also the total residence time which varies between 0.61 and 0.88 of measured value.
Comparison between measured settling velocity and settling velocity calculated with Eq. (7) for sample data E2.6%d2. Grey dashed lines A, B, C show vertical locations described in text
Trajectory and orientation pattern
Figure 5 shows the sample trajectories of disks retrieved from the view of settling particle recorded by camera#1 (x, z) and camera#2 (y, z) with the indication of characteristic velocity points and onsets of phases II, III, and IV. 2D positions of particle centre in the pairs of images, shown in Fig. 5b, c, e, f, h, i, were combined to get 3D trajectories of settling disks shown in corresponding plots in Fig. 5a, d, g. It could be seen from Fig. 5 that in phases I and III, when a disk settles in a horizontal and vertical position, respectively, a particle tends to settle in a vertical path. Some deviation from the perfect vertical path is observed as the effect of tilting of particles which could be due to unavoidable imperfections of manufactured particles (uneven surface, location of the centre of mass) which affect settling dynamics in a low-inertia motion. Nonetheless, settling could be considered as vertical. On the other hand, in reorientation phases II and IV, the particle moves in a horizontal plane as the effect of particle inclination with respect to the gravity.
The extent of particle horizontal drift was assessed as the Euclidean distance. Figure 6 presents the variation of distance travelled by the centre of particle mass with respect to its initial position in a horizontal plane. The results show very good repeatability of settling behaviour in phase II, while some discrepancies (deviation from vertical settling) are observed for phase III similarly to the above analysis of data presented in Fig. 5.
The analysis of 3D data shows that particles do not descend in a plane along the whole path (Figs. 5, 6). While the settling in phases I–III could be considered as planar, the disk may change the plane of settling in a second reorientation phase (phase IV), since there is no preferential direction of horizontal drift during this phase. It causes the translation of particle with respect to its initial position in a horizontal plane and consequently affects the extent of dispersion of particles.
Plots in Fig. 7 show the horizontal dispersion of particles in the x–y plane. It is clear from the figure that there is no preferential direction of reorientations, which results in a random final position of particle with respect to the initial position. Horizontal drift is attributed to reorientation phases and has not exceeded 0.01 m along the vertical distance (0.077 m) analysed in this study. It should be noted that the fact that particles do not fall in a plane affects the variance of horizontal drift results.
The results reveal some trends in horizontal dispersion when particle diameter is considered. Figure 8 presents the comparison between an average horizontal drift for two sets of particles. The comparison between a drift in phases I and II and the total drift in considered paths indicates that the second reorientation contributes to the horizontal drift to a larger extent than the first one; that is, a particle travels larger horizontal distance in phase IV in which rotation is accompanied with gliding motion than in phase II. The results indicate that d3 disks tend to travel larger distance in a horizontal direction compared to d2 disks; hence, greater dispersion may be expected for disks with a larger diameter given the same stratification conditions. The effect of stratification strength on particle dispersion is not clear.
Analysis of parameters for characteristic minimum velocities and onsets of reorientation
Settling velocity decreases significantly when a particle is translating across a density transition from terminal settling value in an upper layer, Uul, to the first minimum settling velocity, umin1, within the transition layer. Velocity reduction is more pronounced for larger particles (see Figs. 9 and 10) with umin1/Uul ranging between 0.05 and 0.08 for disks d3, while it is within the range (0.14; 0.19) for d2. Moreover, the ratio between umin1 for d3 and d2 is less than 75%, indicating that d3 achieves smaller local settling velocity after crossing the interface than d2. It could be explained by the fact that a disk falling with its face normal to gravity in the upper part of transition region starts to experience additional stratification-induced drag. This drag is associated with the entrainment of lighter fluid into the wake of settling disk (see Fig. 3 in (Mrokowska 2018)). Since a disk with larger diameter is able to entrain larger volume of lighter fluid, the added-buoyancy effect increases with the particle dimensions, which implies larger drag and velocity reduction. On the other hand, local minimum velocity umin2 does not vary significantly between the two types of particles for the same conditions in density transition, indicating that settling velocity is not so sensitive on particle geometry when it descends in vertical position.
It is expected that the parameters for characteristic points within the density transition (the first and the second local minima and reorientation points) depend on the settling characteristics in the upper layer and the characteristics of stratification. Four depth-dependent parameters describing settling conditions within the transition layer relevant in this study problem have been analysed (Eqs. 3–6): Re(z), Fr(z), Ar(z), Re(z)/Fr(z) and the entrance Re number, Reul was considered to elucidate how settling dynamics is affected by the stratification and characteristics of settling dynamics in the upper layer.
To get insight into the particle dynamics, the evolution of Re number with depth has been analysed. While Re number assumes constant values in the upper layer between 5.0 and 11.1 depending on experimental conditions (particle diameter and fluid density) (Table 2), it varies with depth within the transition layer following the pattern of settling velocity. Re number achieves two local minima corresponding with settling velocity minima dropping to the minimum Re ~ 1 for all considered particles. Reynolds number corresponding to the first minimum velocity, Reumin1, achieves smaller values for larger disks; Reumin1 is within the range (0.92, 1.1) for d3 and within the range (0.48, 0.89) for d2 disks. Related observation for velocity is presented in Fig. 10 and described above. Observations for Reumin2 are in line with that for umin2, that is, disk dimensions do not have significant impact on Reumin2. Results presented in this study show that the onset of reorientation from the stable horizontal to stable vertical position overlaps with the minimum settling velocity, umin1. Since Re number drops significantly at this point to values close to unity or even smaller, the reduction in inertial effects enables buoyancy-induced torques to overcome pressure-induced torques. Particles accelerate when descending in the transition in a vertical position as a result of diminishing stratification strength (Fig. 3), and Re number increases accordingly. However, disks are able to keep stable vertical position up to relatively high Re (in some tests ~ 6) despite growing effect of inertia, which indicates that density gradients effectively overcome pressure-induced torques.
Another relevant parameter, Froude number, varies with depth between infinity in homogeneous layers to finite values within the transition layer. Fr achieves the minimum in the region where buoyancy frequency assumes the highest values and the particle decelerates considerably, indicating that the stratification dominates over inertia. Considering all experimental sets, minimum Froude number varies between 0.05 and 0.06 for d2 and between 0.02 and 0.03 for d3, suggesting greater influence of stratification on a disk with a larger diameter. Fr number increases up to Fr ~ 5 at the lower border of transition where N = 0.2 s−1, and then it increases to infinity in a homogeneous layer.
Archimedes number decreases monotonically from a constant value in an upper layer (between 3.5 and 6.2 in considered experimental sets) to 2.2 and 3.3 for d2 and d3, respectively, in the lower layer showing a great dependence on density difference between the fluid and the particle.
The relation between settling dynamics in an upper layer, characterised by Reul, and characteristic values of parameters Fr(z), Re(z)/Fr(z), Ar(z) corresponding to settling velocity minima, denoted here by a subscript “c”, were analysed, and the results are presented in Fig. 11. Plots show a decreasing trend for Frumin1 versus Reul and increasing trend for Arumin1 versus Rul and Reumin1/Frumin1 versus Rul, indicating that these relations may be good candidates to elucidate threshold values for the onset of the first reorientation (and occurrence of the first minimum velocity). These results indicate that settling dynamics in the upper layer, stratification characteristics in the transition layer, and particle dimensions affect characteristic minimum velocities and the onset of reorientation which is compatible with umin1. However, more data sets for wider range of conditions are necessary to define a functional relationship.
Similar relationships are observed for parameters Frumin2, Reumin2/Frumin2, and Arumin2; however, trends are weaker, showing that the occurrence of the second velocity minimum is less sensitive to the settling conditions in the upper layer than the first minimum velocity. No clear dependence was observed between characteristic Reynolds number and entrance Re number.
Conclusions
Settling dynamics of thin disks descending through a nonlinear density transition were studied experimentally. The results have demonstrated that complex hydrodynamic interactions between a particle and a liquid lead to settling orientation instabilities and unsteady particle descent. The most interesting aspects of disk settling through the density transition are conditions necessary for reorientation, the pattern of non-monotonous velocity with focus on local minima in the second and third phase, and the horizontal drift of particles.
Relations between entrance Reynolds number, Reul, and Re/Fr, Ar, and Fr were identified for characteristic points (settling velocity local minima and the first reorientation), indicating settling conditions in an upper layer, the stratification strength of transition, and particle dimension control settling dynamics within the transition layer.
The condition for reorientation from a stable horizontal to stable vertical position is of particular interest, which has been analysed for linear stratification in other research (Mercier et al. 2020). Results presented herein show that a particle keeps a horizontal position within nonlinear density transition up to a point where the particle achieves the first local minimum and the onset of reorientation has been attributed to Re number low enough to let stratification effects overcome inertial ones.
The comparison of settling dynamics of thin disks with two different diameters showed that the dynamics are sensitive to a particle diameter mainly in the upper part of density transition with a non-obvious result that a larger disk settling with higher terminal velocity in the upper layer achieves smaller first minimum velocity than disk with a smaller diameter. Settling dynamics of two types of disks within a transition layer does not vary considerably in terms of settling velocity with negligible difference in the second minimum velocity. All these results suggest that geometry of particles should be carefully considered to assess settling dynamics just after crossing a density interface, since small deviations in geometry may affect settling parameters.
Fundamental understanding of dynamics of individual particles in stratified systems is critical for further elucidation of physical mechanisms of particle groups settling necessary to develop prediction methods for sedimentation flux and descent of immotile microorganisms. Specifically, the knowledge on settling dynamics within transition layer may improve the understanding of thin layers formation, since one of reasons for little understanding of this process is our scarce knowledge on the dynamics of non-spherical particles and effects of stratification. The results showed that disks experience horizontal drift in reorientation phases (phase II and IV) and fading stratification in phase IV and a gliding motion of particle in this phase play the major role in horizontal dispersion of particles. This fact may be important in a wider context when a group of disks settles and may interact with each other, e.g. a group of disk-shaped diatoms in the ocean. Since the dispersion of particles is expected in the lower part of transition, interactions between particles are likely to be intensified in this region.
It has been demonstrated that parameters critical to estimate particulate flux, namely the residence time of particles in a water column and settling velocity, are misestimated by conventionally used approaches which do not take into account the dynamics of non-spherical particles in stratified systems. Settling behaviour of particles within the transition layer has impact not only on the prolonged residence of particles at pycnoclines which may lead to the formation of thin layers, but also increases the total residence time of particles in a water column, which is of importance to the estimation of sedimentation rate, carbon transport, as well as other biogeochemical processes.
Density transitions occurring commonly in natural waters are much thicker compared to the dimensions of settling particles and could be considered as linear; nonetheless, the results presented herein reveal physical mechanisms that could explain settling behaviour of solid particles in nature. Although a vast amount of particles present in the environment is of non-spherical shapes including disks, a few research performed so far (Doostmohammadi and Ardekani 2014; Mercier et al. 2020; Mrokowska 2018) indicated that the settling dynamics including orientation instabilities and non-monotonous settling velocity are more important than probably previously thought. Hence, present challenge is to incorporate the geometry of non-spherical particles into the analysis of settling behaviour of particles in background stratification, since the variation of particle orientation with its descent highly affects settling velocity due to orientation-dependent drag.
This study is constrained to the limited experimental conditions, i.e. particle characteristics and stratification parameters; only a disk diameter was variable while thickness was kept constant. The relationships between settling parameters could be different for disks with different aspect ratio which should be considered in further studies. More experimental results on disks settling through a density transition are necessary to find parameter ranges characteristic for various behaviours of disks settling in a low to moderate Re numbers. Wider range of experimental conditions should be considered to investigate some limiting cases in density transition with a nonlinear stratification to quantify conditions governing the onset of stratification-induced reorientations. Moreover, development of numerical models is necessary to facilitate laboratory experiments due to their limited capacity.
Data availability
Data available upon request to the author.
References
Abaid N, Adalsteinsson D, Agyapong A, McLaughlin RM (2004) An internal splash: levitation of falling spheres in stratified fluids. Phys Fluids 16:1567–1580. https://doi.org/10.1063/1.1687685
Ardekani AM, Doostmohammadi A, Desai N (2017) Transport of particles, drops, and small organisms in density stratified fluids. Phys Rev Fluids 2:100503. https://doi.org/10.1103/PhysRevFluids.2.100503
Arnosti C (2011) Microbial extracellular enzymes and the marine carbon cycle. Annu Rev Mar Sci 3:401–425. https://doi.org/10.1146/annurev-marine-120709-142731
Auguste F, Magnaudet J, Fabre D (2013) Falling styles of disks. J Fluid Mech 719:388–405. https://doi.org/10.1017/jfm.2012.602
Bagheri G, Bonadonna C (2016) On the drag of freely falling non-spherical particles. Powder Technol 301:526–544. https://doi.org/10.1016/j.powtec.2016.06.015
Blanchette F, Shapiro AM (2012) Drops settling in sharp stratification with and without Marangoni effects. Phys Fluids 24:042104. https://doi.org/10.1063/1.4704790
Camassa R, Falcon C, Lin J, McLaughlin RM, Mykins N (2010) A first-principle predictive theory for a sphere falling through sharply stratified fluid at low Reynolds number. J Fluid Mech 664:436–465. https://doi.org/10.1017/s0022112010003800
Camassa R, Falcon C, Lin J, McLaughlin RM, Parker R (2009) Prolonged residence times for particles settling through stratified miscible fluids in the Stokes regime. Phys Fluids 21:031702. https://doi.org/10.1063/1.3094922
Capet A, Stanev EV, Beckers JM, Murray JW, Gregoire M (2016) Decline of the Black Sea oxygen inventory. Biogeosciences 13:1287–1297. https://doi.org/10.5194/bg-13-1287-2016
Clift R, Grace JR, Weber ME (1978) Bubbles, drops, and particles. Academic Press, Cambridge
Cole M, Lindeque P, Halsband C, Galloway TS (2011) Microplastics as contaminants in the marine environment: a review. Mar Pollut Bull 62:2588–2597. https://doi.org/10.1016/j.marpolbul.2011.09.025
D'Asaro E (2018) Oceanographic floats: principles of operation. In: Venkatesan R, Tandon A, D'Asaro E, Atmanand MA (eds) Observing the oceans in real time. Springer, Cham, pp 77–98. https://doi.org/10.1007/978-3-319-66493-4_5
Dey S, Ali SZ, Padhi E (2019) Terminal fall velocity: the legacy of Stokes from the perspective of fluvial hydraulics. Proc R Soc A-Math Phys Eng Sci 475:20190277. https://doi.org/10.1098/rspa.2019.0277
Diercks A, Ziervogel K, Sibert R, Joye SB, Asper V, Montoya JP (2019) Vertical marine snow distribution in the stratified, hypersaline, and anoxic Orca Basin (Gulf of Mexico). Elementa-Sci Anthrop 7:1. https://doi.org/10.1525/elementa.348
Dietrich WE (1982) Settling velocity of natural particles. Water Resour Res 18:1615–1626. https://doi.org/10.1029/WR018i006p01615
Doostmohammadi A, Ardekani AM (2014) Reorientation of elongated particles at density interfaces. Phys Rev E 90:033013. https://doi.org/10.1103/PhysRevE.90.033013
Doostmohammadi A, Dabiri S, Ardekani AM (2014) A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J Fluid Mech 750:5–32. https://doi.org/10.1017/jfm.2014.243
Doostmohammadi A, Stocker R, Ardekani AM (2012) Low-Reynolds-number swimming at pycnoclines. Proc Natl Acad Sci USA 109:3856–3861. https://doi.org/10.1073/pnas.1116210109
Field SB, Klaus M, Moore MG, Nori F (1997) Chaotic dynamics of falling disks. Nature 388:252–254. https://doi.org/10.1038/40817
Kestin J, Khalifa HE, Correia RJ (1981) Tables of the dynamic and kinematic viscosity of aqueous NaCl solutions in the temperature-range 20–150-degrees-C and the pressure range 0.1–35 MPa. J Phys Chem Ref Data 10:71–87
Khatmullina L, Isachenko I (2017) Settling velocity of microplastic particles of regular shapes. Mar Pollut Bull 114:871–880. https://doi.org/10.1016/j.marpolbul.2016.11.024
Kindler K, Khalili A, Stocker R (2010) Diffusion-limited retention of porous particles at density interfaces. Proc Natl Acad Sci USA 107:22163–22168. https://doi.org/10.1073/pnas.1012319108
Lam T, Vincent L, Kanso E (2019) Passive flight in density-stratified fluids. J Fluid Mech 860:200–223. https://doi.org/10.1017/jfm.2018.862
Laurenceau-Cornec EC, Le Moigne FAC, Gallinari M et al (2019) New guidelines for the application of Stokes' models to the sinking velocity of marine aggregates. Limnol Oceanogr 9999:1–22. https://doi.org/10.1002/lno.11388
Loth E (2008) Drag of non-spherical solid particles of regular and irregular shape. Powder Technol 182:342–353. https://doi.org/10.1016/j.powtec.2007.06.001
Lutz M, Dunbar R, Caldeira K (2002) Regional variability in the vertical flux of particulate organic carbon in the ocean interior. Global Biogeochem Cycles 16(3):1037. https://doi.org/10.1029/2000gb001383
Macintyre S, Alldredge AL, Gotschalk CC (1995) Accumulation of marine snow at density discontinuities in the water column. Limnol Oceanogr 40:449–468. https://doi.org/10.4319/lo.1995.40.3.0449
Maggi F (2013) The settling velocity of mineral, biomineral, and biological particles and aggregates in water. J Geophys Res-Oceans 118:2118–2132. https://doi.org/10.1002/jgrc.20086
Magnaudet J, Mercier MJ (2020) Particles, drops, and bubbles moving across sharp interfaces and stratified layers. Annu Rev Fluid Mech 52:61–91. https://doi.org/10.1146/annurev-fluid-010719-060139
Mercier MJ, Wang S, Pemeja J, Ern P, Ardekani AM (2020) Settling disks in a linearly stratified fluid. J Fluid Mech 885:A2. https://doi.org/10.1017/jfm.2019.957
Mrokowska MM (2018) Stratification-induced reorientation of disk settling through ambient density transition. Sci Rep 8:412. https://doi.org/10.1038/s41598-017-18654-7
Mrokowska MM, Krztoń-Maziopa A (2019) Viscoelastic and shear-thinning effects of aqueous exopolymer solution on disk and sphere settling. Sci Rep 9:7897. https://doi.org/10.1038/s41598-019-44233-z
Noufal KK, Najeem S, Latha G, Venkatesan R (2017) Seasonal and long term evolution of oceanographic conditions based on year-around observation in Kongsfjorden, Arctic Ocean. Polar Sci 11:1–10. https://doi.org/10.1016/j.polar.2016.11.001
Okino S, Akiyama S, Hanazaki H (2017) Velocity distribution around a sphere descending in a linearly stratified fluid. J Fluid Mech 826:759–780. https://doi.org/10.1017/jfm.2017.474
Peperzak L, Colijn F, Koeman R, Gieskes WWC, Joordens JCA (2003) Phytoplankton sinking rates in the Rhine region of freshwater influence. J Plankton Res 25:365–383. https://doi.org/10.1093/plankt/25.4.365
Prairie JC, White BL (2017) A model for thin layer formation by delayed particle settling at sharp density gradients. Cont Shelf Res 133:37–46. https://doi.org/10.1016/j.csr.2016.12.007
Prairie JC, Ziervogel K, Camassa R et al (2015) Delayed settling of marine snow: effects of density gradient and particle properties and implications for carbon cycling. Mar Chem 175:28–38. https://doi.org/10.1016/j.marchem.2015.04.006
Prairie JC, Ziervogel K, Camassa R et al (2017) Ephemeral aggregate layers in the water column leave lasting footprints in the carbon cycle. Limnol Oceanogr Lett 2:202–209. https://doi.org/10.1002/lol2.10053
Raffaele L, Bruno L, Sherman DJ (2020) Statistical characterization of sedimentation velocity of natural particles. Aeol Res. https://doi.org/10.1016/j.aeolia.2020.100593
Renggli CJ, Wiesmaier S, De Campos CP, Hess KU, Dingwell DB (2016) Magma mixing induced by particle settling. Contrib Miner Petrol 171(11):96. https://doi.org/10.1007/s00410-016-1305-1
Saxby J, Beckett F, Cashman K, Rust A, Tennant E (2018) The impact of particle shape on fall velocity: Implications for volcanic ash dispersion modelling. J Volcanol Geoth Res 362:32–48. https://doi.org/10.1016/j.jvolgeores.2018.08.006
Scase MM, Dalziel SB (2004) Internal wave fields and drag generated by a translating body in a stratified fluid. J Fluid Mech 498:289–313. https://doi.org/10.1017/s0022112003006815
Srdic-Mitrovic AN, Mohamed NA, Fernando HJS (1999) Gravitational settling of particles through density interfaces. J Fluid Mech 381:175–198. https://doi.org/10.1017/s0022112098003590
Turner JT (2015) Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump. Prog Oceanogr 130:205–248. https://doi.org/10.1016/j.pocean.2014.08.005
Verso L, van Reeuwijk M, Liberzon A (2019) Transient stratification force on particles crossing a density interface. Int J Multiph Flow. https://doi.org/10.1016/j.ijmultiphaseflow.2019.103109
Waldschlager K, Schuttrumpf H (2019) Effects of particle properties on the settling and rise velocities of microplastics in freshwater under laboratory conditions. Environ Sci Technol 53:1958–1966. https://doi.org/10.1021/acs.est.8b06794
Willmarth WW, Hawk NE, Harvey RL (1964) Steady and unsteady motions and wakes of freely falling disks. Phys Fluids 7:197–208. https://doi.org/10.1063/1.1711133
Woods AW (1995) The dynamics of explosive volcanic-eruptions. Rev Geophys 33:495–530. https://doi.org/10.1029/95rg02096
Yick KY, Torres CR, Peacock T, Stocker R (2009) Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J Fluid Mech 632:49–68. https://doi.org/10.1017/s0022112009007332
Zhai L, Sun ZB, Li ZM et al (2019) Dynamic effects of topography on dust particles in the Beijing region of China. Atmos Environ 213:413–423. https://doi.org/10.1016/j.atmosenv.2019.06.029
Funding
This work was supported within an internal grant of Institute of Geophysics, Polish Academy of Sciences No. 7a/IGF PAN/2018mł and partially within statutory activities No. 3841/E-41/S/2020 of the Ministry of Science and Higher Education of Poland.
Author information
Authors and Affiliations
Contributions
Magdalena Mrokowska is the sole author of the present study; she conceived the study, performed experiments, processed data, analysed results, and wrote the paper.
Corresponding author
Ethics declarations
Conflict of interest
The author declares no competing interests.
Code availability
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mrokowska, M.M. Dynamics of thin disk settling in two-layered fluid with density transition. Acta Geophys. 68, 1145–1160 (2020). https://doi.org/10.1007/s11600-020-00455-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11600-020-00455-8