Introduction

Disentangling the historical variability of precipitation is key to forecasting, water resources management and flood risk preparedness (Maggioni et al. 2013; Tarek et al. 2017). This is especially true in southern Africa where summer floods are described as ‘a way of life’. In fact, rainfall and water related disasters are documented as one of the most damaging environmental risks of the twenty-first century (Miceli et al. 2008). To minimise these losses, accurate measurement of precipitation before input into any hydrological or forecasting system is crucial. Although many meteorological variables require specialist know-how and skill to measure, difficulties with accurate measurements and forecasting are particularly acute with rainfall. This is because precipitation is intrinsically heterogeneous in space and time. Although there is a difference in the scientific definition of rainfall and precipitation (WMO 2010; Met Office 2018), they are used interchangeably in this study.

In many developing countries, access to quality data is a challenge (Awange et al. 2016; Mahmood et al. 2017). This is because meteorological and hydrological stations are usually characterised by low rain gauge distribution to area ratios coupled with infrequent observations (Agnihotri et al. 2015; Basheer et al. 2018). This has also augmented hindrances of advances in climate science across many developing nations. Advancing the availability of climate data in developing countries has the potential of facilitating research that will respond to disastrous extreme events, climate-induced health hazards, and ultimately socio-economic development (Washington et al. 2006; Thomson et al. 2011).

While there are different types of rain gauges (see WMO 2010), in Zambia, precipitation is generally measured using World Meteorological Organization (WMO) standard ordinary rain gauges once every 24 h. These rain gauges are point based and record only the amount of rainfall falling over them. This poses a challenge to having a continuous quality-controlled data set because mostly, these gauges are sparsely located and apart from Provincial Meteorological stations (PMSs), most of them are manned by only one observer (One-manned stations). It is important to note that the Zambia Meteorological Department (ZMD) a specialised organ of the government of the Republic of Zambia in charge of weather and climate monitoring only runs ten PMSs. Therefore, most of the remaining stations are manned by only one observer. This highlights the poor staffing levels of ZMD like in many other developing countries. One-manned stations hinder effective weather and climate monitoring especially in times of ill health. This in turn hampers operational water management and flood forecasting. To overcome this challenge, the use of automatic weather stations to supplement existing manned meteorological stations is being adopted in some countries across Africa (TAHMO 2018). This has future potential to further climate research based on quality observational data sets. In the meantime, scientists employ satellite estimates in many studies around the world. For example, Stampoulis et al. (2013) used satellite data to analyse heavy rainfall events over the Mediterranean, and most recently, Zambrano-Bigiarini et al. (2017) studied the behaviour of satellite rainfall across the complex Chilean topography.

Many research organisations (e.g. The Climatic Research Unit of the University of East Anglia) have developed satellite-based rainfall products (SRPs) to, in part, overcome the challenges of data-scarce regions. The usefulness of SRPs for water management and flood-risk preparedness requires an extensive validation process because generally, SRPs have uncertainties which may cause inaccuracies in flood forecasting and/or model simulations. Many scientists (e.g. Bajracharya et al. 2015; Tarek et al. 2017) have studied SRPs side by side with rain gauge data to understand their ability to capture rain gauge data trends in domains of their interest. These validation studies have also been done, because for effective water resources management and flood forecasting, understanding the precise amount of water entering a catchment or region is crucial as this adds up to antecedent conditions which potentially leads to pluvial and fluvial flooding (Chen et al. 2010; Blanc et al. 2012). Therefore, accurate measurements of rainfall are a key contribution to the advancement of flood forecasting.

While SRPs validation studies have been done in many countries around the world, to our knowledge, none exist for the case of Zambia. To this end, the overall goal of this paper is to evaluate four daily SRPs (i.e. TAMSATv3, PERSIANN, CHIRPSv2.0, and ARCv2) covering the period 1998–2015. Daily SRP data sets were selected, because they provide vital information for decision making processes in flood forecasting (Kar et al. 2015; Tshimanga et al. 2016; Sonkoué et al. 2019) and food security (Stern et al. 1982; Watson and Challinor 2013) that cannot be realised with monthly data sets. This is because most hydrological and agricultural modelling approaches that are used require daily rainfall as an input (Challinor et al. 2004; Clark et al. 2011). These SRPs have been discussed at lengthy in “Data” of this paper. The study period was chosen, because it represents better consistence in station data availability. Results of this study will fill a critical research knowledge gap; particularly, they will strengthen our understanding of the suitability of using SRPs as cost-effective substitutes for daily precipitation measurements in Zambia. Of interest will be the ability of SRPs to mimic rain gauge data across the complex Zambian topography. The findings will also highlight strengths and weaknesses of SRPs (see “Data”) which will be useful for developers of these rainfall estimation products.

Study area and climatology

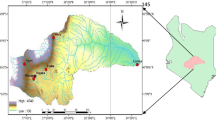
Zambia is a southern African country bounded by latitudes 8°–18° S and longitudes 21.8°–34° E. It is land-linked and covers an area of 752,614 km2 (Limao and Venables 2001). Much of the country is on the central African plateau at an average altitude of 1200 m above mean sea level (Libanda et al. 2018). It has a population of nearly 15 million people (CSO 2010). The inset in Fig. 1 shows the location of Zambia on the map of Africa, while the main figure shows the topographical map of the country. Table 1 presents the longitude, latitude, World Meteorological Organization Station Number and observational frequency of each station.

Fig. 1
figure 1

Topographical (m) map of Zambia with red asterisks showing meteorological station density. Inset shows the location of Zambia (green square) on the Map of Africa. Topographical data are based on the 15 arcsecond resolution (~ 500 m) SRTM15 Plus which is a fusion of Shuttle Radar Topography Mission (SRTM) land topography with measured and estimated seafloor topography (Becker et al. 2009)

Full size image
Table 1 Stations used in the study with their longitude, latitude, elevation and WMO numbers
Full size table

Zambia experiences a sub-tropical climate. The year-to-year mean accumulative rainfall varies greatly over the country with most areas receiving between 800 and 1200 mm (Hachigonta et al. 2008). The country receives most of these rains during the summer months of November to March with October and April being months of transition; the rain season is therefore, clearly defined.

Pioneering studies (e.g. Huygen 1989) on synoptic-scale mechanisms and local features affecting the behaviour of rainfall over Zambia suggest that water bodies, e.g. Lake Mweru which covers 5120 km2 in the Northern half of the country, significantly contributes to boosting localised rainfall over some parts of northern Zambia. In similar studies elsewhere, potential evaporation has been documented to be directly correlated to the amount of water available (Majidi et al. 2015). Many studies have also highlighted the cause-and-effect relationship of evaporation, cloud formation, and localised precipitation (Lee et al. 2015).

Data

Gauge data

The rain gauge data used in this study was kindly provided by the Zambia Meteorological Department (ZMD). ZMD is a specialised organ of the government of the Republic of Zambia in charge of weather and climate monitoring. Even though ZMD was officially recognised as a specialised organ of the Zambian government in January 1967, meteorological and climatological data collection and archiving started in the 1950s under the administration of the Federal Meteorological Services comprising of Nyasaland (Malawi), Northern Rhodesia (Zambia) and Southern Rhodesia (Zimbabwe; Mudenda and Nkonde 2018; ZMD 2020). Daily precipitation data (1998–2015) from 35 meteorological stations (Fig. 1 and Table 1) archived by ZMD was studied sided by side with 4 satellite-based rainfall products (SRPs) to understand the possibility of using SRPs in future research lines to cover data-sparse regions of the country. From “ARCv2” to “PERSIANN”, we give an overview of these SRPs.

ARCv2

Africa Rainfall Climatology Version 2 (ARCv2) was obtained from the archives of the Climate Prediction Centre (CPC) an organ of the National Oceanic and Atmospheric Administration (NOAA); it is freely available here https://iridl.ldeo.columbia.edu. This data set is a blend of geostationary infrared (IR) data sourced from the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) and daily gauge data from the Global Telecommunication System (GTS). ARCv2 is gridded at a spatial resolution of 0.1° × 0.1°, and it is available, in netcdf format, for the period 1983–near present (Novella and Thiaw 2013). It is important to note that as of March 2018, ARCv2 contained 341 days with missing data. This creates a data gap in the evaluation period considered in this study. To facilitate ease comparisons of ARCv2 with other data sets, this gap was filled using Kriging as discussed in the methodologies section.

CHIRPSv2.0

The Climate Hazards Group InfraRed Precipitation with Station data version 2 data set (CHIRPSv2.0: Funk et al. (2015) was also used. This data set is a result of the combined effort of the University of California and the United States Geological Survey (USGS). The data set covers latitudes 50°S–50°N and all longitudes. CHIRPS is a merge of 0.05° × 0.05° resolution satellite imagery and in situ gauge data. The satellite imagery is sourced from the Globally Gridded Satellite (GridSat) data set of the National Climate Centre of NOAA. As in ARCv2, in situ gauge data are sourced from the GTS. Some in situ gauge data are also contributed by the Southern Africa Service Centre for Climate Change and Adaptive Land Management (SASSCAL), Global Historical Climate Network (GHCN), and the Global Summary of the Day (GSOD). A detailed description of this data set is available in the work of Funk et al. (2015) and here: https://chg.geog.ucsb.edu/data/chirps/.

TAMSATv3

TAMSATv3 (Tropical Applications of Meteorology using Satellite and ground-based observations), a product of the University of Reading was also evaluated in this study. It is gridded at a spatial resolution of 0.0375° × 0.0375° and covers the period 1983 to near-present. The primary sources of data for the development of TAMSAT are the Meteosat IR imagery from EUMETSAT and rainfall data from in situ rain gauges. The Meteosat imagery used was retrieved every 30 min prior to mid-2006 and every 15 min thereafter. Maidment et al. (2017) describes this data set in detail. Further information can also be found online at: https://www.tamsat.org.uk/data/archive.

PERSIANN

Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks-Climate Data Record (PERSIANN; Ashouri et al. 2015) was also examined. PERSIANN is a product of the National Climatic Data Center (NCDC), a technical organ of NOAA. This product is gridded at a spatial resolution of 0.25° × 0.25° covering latitudes 60° S and 60° N and all longitudes. The data set is available for the period 1983 to near-present. PERSIANN is a direct product of an artificial neural network model. To calibrate the model, hourly precipitation data were sourced from the National Center for Environment Prediction (NCEP) and to run it, IR imagery was sourced from GridSat. The final product was bias corrected using the Global Precipitation Climatology Project (GPCP) data set. The work of Ashouri et al. (2015) describes this data set in detail with additional information provided online at: https://climatedataguide.ucar.edu/climate-data/persiann-cdr-precipitation-estimation-remotely-sensed-information-using-artificial.

Statistical methodologies

The comparative methods employed herein involved the use of SRPs for only the grid cells containing rain gauges. To avoid augmenting errors, stations that had less than 80% observational frequency were excluded. SRPs data for these stations were also not considered. This brought the total number of stations that were used for further analyses to 35. The geographical location of these stations together with their elevation and frequency of observations is given in Table 1.

The 35 stations were then subjected to a standard normal homogeneity test (SNHT) with the aim of removing any influence that may have been exerted by inhomogeneities. Inhomogeneous data can be a result of changes in measurement approaches, changes in instrumentation or location of observatory stations. Although, there are many methods of testing homogeneity, SNHT is the commonly used method in hydrometeorological research (Alexandersson et al. 1997). Mathematically, SNHT is given as:

$$T_{y} = y\overline{{z_{1} }} + (n - y)\overline{{z_{2} }} ,\quad y = 1,2, \ldots ,n$$
(1)

where:

$$\overline{{z_{1} }} = \frac{1}{y}\sum\limits_{i = 1}^{n} {\frac{{(Y_{i} - \overline{Y)} }}{S}} \quad and\quad \overline{{z_{2} }} = \frac{1}{n - y}\sum\limits_{i = y + 1}^{n} {\frac{{(Y_{i} - \overline{Y)} }}{S}}$$
(2)

Ty is a statistic which is used to compare the mean of the first y years with the last of (n − y) years. \(\overline{{Z_{1} }}\) and \(\overline{{Z_{2} }}\) are the values of \(\overline{{Z_{i} }}\) during the first y years and the last (n − y) years, respectively. If the value of T is maximum, the year of y would be considered as having a break. The null hypothesis is rejected if the test

$$T_{0} = \mathop {\max T_{y} }\limits_{1 \le y \le n}$$
(3)

is greater than the critical value, which is dependent on the size of the sample under consideration (Kang et al. 2012). The hypothesis was tested at \(\alpha\) = 0.05 as follows:

H0 is the Data are homogeneous, Ha is the there is a date at which there is a change in the data.

As part of data preparation and before any comparative analyses were done, Climate Data Operators (CDO) were employed in which Kriging was used as in Oliver et al. (1990) to temporally fill in the blanks of missing values. The temporal interpolation was done so that data sets with missing values e.g. ARCv2 would not be disadvantaged during comparative analysis. Although there are many other interpolation methods, Kriging was chosen because previous literature (see for example: Creutin et al. 1982; Tabios et al. 1985; Goovaerts 2000; Maidment et al. 2017) found it to be superior over other forms of interpolation. Kriging weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for kriging is given as:

$${\hat{\text{Z}}}\left( {s_{o} } \right) = \sum\limits_{i = 1}^{n} {\lambda_{i} } Z\left( {s_{i} } \right)$$
(4)

where Z(\(s_{i}\)) is the measured value at the ith location; \(\lambda_{i}\) is an unknown weight for the measured value at the ith location; \(s_{0}\) is the predicted location and N is the number of measured values.

Coefficient of determination (R2) was also explored to quantify the magnitude of how closely SRPs follow rain gauge data. R2 is mathematically defined as the regression sum of squares divided by the total sum of squares and is expressed as:

$$R^{2} = 1 - \frac{{SS_{res} }}{{SS_{tot} }}$$
(5)

where SSres is the residual sum of squares and SStot is the total sum of squares with respect to the variance of the data. The grading of R2 varies between 0 and 1 with 0 denoting that the predictor variable does not explain any of the variation in the dependant variable, while 1 shows that the predictor variable accounts for all of the variation in the dependant variable (Basheer and Elagib 2018).

We further employed percent root-mean-square error (%RMSE) as used by Duan et al. (2012), to examine the reliability of SRPs against rain gauge data. Basically, %RMSE returns values lower than 50% if the data are reliable and greater than 50% if found unreliable. Mathematically, RMSE is expressed as:

$$RMSE = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {(X_{obs,i} - X_{mo\,del,i} )^{2} } }}{n}}$$
(6)

here Xobs is rain gauge data and Xmodel are the SRP data sets at time/place i (Chai et al. 2014). To calculate %RMSE, we divided the RMSE by the mean of rain gauge data. This approach is also available in the work of Duan et al. (2012) who studied the ability of Tropical Rainfall Measurement Mission (TRMM) to simulate rain gauge data in the Caspian Sea Region.

We employed two more statistical measures for annual rainfall estimates; these are the coefficient of variation (CV) and the median (M). The median is best defined as a measure of central tendency while the CV is the ratio of the standard deviation to the mean and as such a good measure of dispersion. It can take any value from zero variability to high variability. Mathematically, the CV is given as:

$$CV(\% ) = \frac{{\sqrt {\frac{{\sum\nolimits_{i}^{n} {(s_{i} - \overline{s}} )}}{n - i}} }}{{\overline{s}}} \times 100$$
(7)

where Si is the ith rainfall estimation in mm, n is the number of data pairs, and \(\overline{s}\) is the average of the rainfall estimates (Basheer and Elagib 2018).

Comparisons were also done for three stations lying at the highest, middle and lowest elevations to examine the ability of SRPs to capture precipitation occurrences on complex topography. Mbala at 1665 m, Kabwe main at 1204 m and Chipepo at 488 m were the highest, middle and lowest elevations, respectively (Table 1).

Methods used herein have been employed by several studies to investigate the possibility of using SRPs in data sparse regions around the world. For example, Bowman (2005) compared TRMM rainfall retrievals with rain gauge data from the TAO/TRITON buoy array. In a similar study He et al. (2017), compared daily rainfall from Global Precipitation Measurement (GPM) and TRMM over the Mekong river basin.

Results and discussion

Daily rainfall

Results of the homogeneity test showed that all stations were homogeneous apart from Lusitu, and it was therefore excluded from further analyses. Statistical results of how closely SRPs match rain gauge data are shown in Table 2. These results are presented as daily rainfall on an annual scale. Notably, SRPs were able to simulate daily means accurately with percent root-mean-square errors of lower than 50% in all cases. Figure 2 presents scatter plots of each SRP against rain gauge data. With an R2 value of 0.96, PERSIANN was the highest performing SRP followed by CHIRPSv2.0 and TAMSATv3.0, respectively. With an R2 value of 0.3, ARCv2 was the lowest performing product. RMSE results further confirm these findings with PERSIANN having lowest RMSE (0.07 mm) followed by CHIRPSv2.0 (0.25 mm), TAMSATv3.0 (0.26 mm) and ARCv2 (0.41 mm), respectively. These results suggest that experiments using daily average rainfall of PERSIANN data are expected to arrive at similar results as those using rain gauge data. The low performance found in ARCv2 has been highlighted by Novella and Thiaw (2013) who attributed it to decreased availability of in situ measurements which leads to a tendency of ARCv2 underestimating rain gauge data.

Table 2 Statistical summary of daily rainfall as obtained from rain gauges (RG), TAMSATv3 (TAM), PERSIANN (PER), CHIRPSv2.0 (CHI), and ARCv2 (ARC)
Full size table
Fig. 2
figure 2

Scatter plot of the average daily rainfall on an annual basis for rain gauge and SRPs data over Zambia, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S for the period 1998–2015. The blue solid lines represent the 1:1 while the red and dashed are the regression lines

Full size image

Although 3 of these SRPs (i.e. PERSIANN, CHIRPSv2.0, and TAMSATv3.0) were able to mimic daily mean rainfall of rain gauge data with R2 values of > 0.5 (Fig. 2), problems were acute with reproducing daily maxima (Fig. 3). All the SRPs did not accurately capture the daily maxima of rainfall. Therefore, caution needs to be taken for experiments considering the use of peaks. It is highly recommended that such experiments take bias correction into account. Generally, SRPs seem to perform better on rainfall averages than maxima in the tropics. Similar results were found by Tarek et al. (2017) who assessed the performance of TRMM in Bangladesh and found good agreement on means and totals but overestimation on maximum values.

Fig. 3
figure 3

Scatter plot of the maximum daily rainfall in each month for rain gauge and SRPs data over Zambia, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015. The blue solid lines represent the 1:1 while the red and dashed are the regression lines

Full size image

Monthly rainfall

In a developing country like Zambia, where both wet and dry spells are common (Hachigonta et al. 2006) and where most people depend on agriculture for a livelihood, a reliable understanding of monthly variations of rainfall is important. Perhaps more important than understanding the annual variations because an understanding of intra-seasonal variations empowers farmers with knowledge that enables them to make informed decisions on sowing and harvesting dates (Hachigonta et al. 2008). It also furnishes hydrometeorologists with vital information for flood preparedness. For these reasons, SRPs were also analysed in terms of their ability to capture the month to month cycle of total rain gauge data. Results (Fig. 4) indicate that all the SRPs were adequately able to reproduce the bimodal rainfall cycle of Zambia with dry periods during the months of May to September and wetness from October to April.

Fig. 4
figure 4

Average monthly rainfall over Zambia for: a rain gauge (blue) versus TAMSATv3 (grey), b rain gauge (blue) versus PERSIANN (black), c rain gauge (blue) versus CHIRPSv2.0 (orange) and d rain gauge (blue) versus ARCv2 (red), averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015

Full size image

Figure 5 presents the scatter plots of each of the four SRPs. These results indicate that all the SRPs mimicked gauge data with R2 > 0.9. To rank their performance, RMSE was examined and it was found that with a value of only 4.6 mm, PERSIANN outperformed the other 3 SRPs, followed by CHIRPSv2.0, TAMSATv3, and ARCv2, respectively. It’s the finding of this study therefore, that although PERSIANN outperforms the other SRPs, they are all reliably able to be used in studies that aim at using monthly rainfall.

Fig. 5
figure 5

Scatter plot of mean monthly rainfall over Zambia for: a rain gauge versus TAMSATv3, b rain gauge versus PERSIANN, c rain gauge versus CHIRPSv2.0, d rain gauge versus ARCv2, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015. The blue solid lines represent the 1:1 while the red and dashed are the regression lines

Full size image

Seasonal rainfall

Even though rains in the dry season are not common, some occasional precipitation activities especially in the winter are experienced in Zambia. Exploratory analyses of rain gauge data further showed that these rains usually amount to less than a millimetre (trace) in 24 h but can accumulate up to 20 mm over the entire dry season. Dry seasons invariably experience sporadic showers over Zambia especially if they follow a strong La Nina which tends to deposit excess moisture over the country.

SRPs were therefore investigated on how closely they follow gauge data during the wet and dry seasons. Results (Fig. 6 left panel) show that these products and rain gauge data are strongly correlated during the wet season with an R2 > 0.5 in all cases except ARCv2 which scored only 0.29. However, the occasional localised rains that fall during the dry season were poorly captured by all SRPs (Fig. 6 right panel) with R2 < 0.5 except PERSIANN which scored ~ 0.8. The observed R2 values are also in agreement with RMSE values i.e. well performing products score high on R2 but low on RMSE. Taken together, PERSIANN outperforms all products followed by CHIRPSv2.0, TAMSATv3 and ARCv2, respectively.

Fig. 6
figure 6

Scatter plot of seasonal rainfall over Zambia for left panel, rainy season and right panel, dry season, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015. The blue solid lines represent the 1:1 while the red and dashed are the regression lines

Full size image

Annual rainfall

SRPs were also examined on their ability to capture variability on an annual basis for the period 1998–2015. Results (Fig. 7) show that all the products were generally able to pick the curves and inter-annual variations of gauge data. It is worth noting that apart from ARCv2, all products detected a downward trend in annual precipitation. At the station level, the trend of annual rainfall is variable, with marginal upward trends generally being statistically insignificant (Chabala et al. 2013) but taken together over Zambia, there is a statistically significant downward trend (Libanda et al. 2018). The inability of ARCv2 to reproduce the decreasing trend of annual rainfall over Zambia is again reflected in the R2 value as it is the only product with a value less than 0.5 and RMSE greater than 100 mm (Fig. 8d).

Fig. 7
figure 7

Comparison of annual rainfall over Zambia for rain gauge data (thick red curve), TAMSATv3 (black), PERSIANN (grey), CHIRPSv2.0 (blue), and ARCv2 (green), averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015

Full size image
Fig. 8
figure 8

Scatter plot of annual rainfall over Zambia over Zambia for left panel, rainy season and right panel, dry season, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015. The blue solid lines represent the 1:1 while the red and dashed are the regression lines

Full size image

It is notable that although the performance of SRPs at seasonal (Fig. 6) and annual (Fig. 8) scales is similar, R2 values of annual rainfall compared to seasonal rainfall are lowered slightly while RMSE values increase owing to the general poor performance of SRPs during dry season.

Given the surprising results in terms of annual rainfall trend direction exhibited by ARCv2 (Fig. 7), two more statistical measures, coefficient of variation (CV) and median (M), were employed to assess all the SRPs at annual scales. CV is a measure of dispersion while median is a measure of central tendency when dealing with variable rainfall (Ananthakrishnan and Soman 1989). These statistical measures are widely used in validation studies of SRPs. For example, recently, Basheer and Elagib (2018) employed them to validate SRPs in a data-scarce South Sudan. In this study, our findings (Table 3) indicate that PERSIANN outperforms all the other products. CHIRPSv2.0 is rated second followed by TAMSATv3 and lastly ARCv2.

Table 3 Coefficient of variation (CV) and median (M) for SRPs and rain gauge data, averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015
Full size table

SRPs were further studied on their ability to capture annual extreme events. This was done by removing influences of dispersion, computing and plotting normalised anomalies of both SRPs and rain gauge observations. Many studies have argued that normalised anomalies are a useful measure of how intense an event was (Ogwang et al. 2012; Chanda and Maity 2015; Libanda et al. 2019). Results (Fig. 9) show that all the SRPs are generally able to mimic the direction better than the magnitude. Rain gauges show that during the period 1998–2015, Zambia received 2 extreme wet events i.e. rainfall ≥ 1 and 4 extreme dry events i.e. ≤ −  1. The extreme wet years were 2000 and 2006 while 2002, 2005, 2013, and 2015 were generally extremely dry. We found that PERSIANN is the only data set that captures this pattern correctly. Other data sets e.g. ARCv2 and CHIRPSv2.0 show mixed signals; in some years, e.g. 2013, they underestimate rain gauge data by ~ 50% while in others, e.g. 2001, they overestimate it. TAMSATv3 tends to overestimate rain gauges. For example, in 2004, it detects an extreme wet event while rain gauge data and PERSIANN do not. The tendency of TAMSATv3 to overestimate rain gauges mirrors the findings of other studies around the world that have highlighted that generally some SRPs overestimate rain gauge data which results in false alarms (Nasrollahi 2015). This is why many studies (e.g. Shen et al. 2010; AghaKouchak et al. 2012) have devoted time to the validation of satellite-based precipitation observations.

Fig. 9
figure 9

Normalised anomalies for TAMSATv3 (black), PERSIANN (grey), CHIRPSv2.0 (blue), ARCv2 (green), and rain gauge (red), averaged over longitude 21.8° E–34° E and latitudes 18° S and 8° S during the period 1998–2015

Full size image

Overall, these findings indicate that PERSIANN, CHIRPSv2.0 and TAMSAT (in order of suitability) are suitable substitutes for rain gauge data for studies that are interested in mean annual rainfall variability over Zambia. Additionally, studies aiming at understanding annual extremes over the country would arrive at similar results as rain gauge data if they employed PERSIANN.

Complex topography

Generally, Zambia is a high plateau (Haberyan 2018). Much of the landmass falls between 910 and 1370 m above sea level. However, a few areas lie outside this range; for example, areas about the Muchinga escarpment in the central province of Zambia exceed 1800 m. Some areas along the major rivers and in valleys lie below 500 m. This is evident in the north-eastern parts of the country were the high flat land is punctuated by the low-lying areas about the Luangwa river and in the southwestern portions of the country where the low-lying areas of the Kafue river punctuate the plateau. These two rivers flow from the Zambezi river which is the biggest watercourse in the country (Huygen 1989).

Precipitation is one of the most difficult meteorological variables to accurately quantify over rough terrain because of the contributions of convective and topographic influences. In high elevations, airflow gets altered and the amount of sunlight reaching the earth’s surface differs markedly within short distances; consequently, precipitation tends to be boosted in some areas and suppressed in others. This has been collaborated by other studies like Ogwang et al. (2014) who used the International Centre for Theoretical Physics Regional Climate Model to study the influence of topography on East African October to December Climate. Their findings indicated that generally mean rainfall tended to reduce with a reduction in topography while temperature was observed to generally increase.

SRPs were therefore, investigated on their ability to capture rain gauge data over varying topography. Three stations at the highest, medium and lowest topography were selected and used to carry out this analysis. These stations are Mbala at 1665 m, Kabwe main at 1204 m and Chipepo at 488 m (Table 2). Results (Fig. 10) indicate that there is reliable capturing of all the curves at all stations. The wetter months of November–April and the drier months of May–October were accurately captured by all data sets. When R2 and RMSE metrics are taken into consideration, PERSIANN outperforms all the other SRPs. However, R2 of all the SRPs is greater than 0.9. This reaffirms the results highlighted in Fig. 5 that generally all the SRPs perform well at capturing the monthly cycle of precipitation.

Fig. 10
figure 10

Mean monthly rainfall for TAMSATv3 (black), PERSIANN (grey), CHIRPSv2.0 (blue), ARCv2 (green), and rain gauges (red) for the period 1998–2015. Where a shows the geographical location of the stations considered b Mbala, c Kabwe, d Chipepo

Full size image

These results further indicate that spatially, SRPs can adequately mimic rain gauge data. The spatial patterns also indicate that SRPs can accurately capture the drier areas of the southern parts of the country and the wetter northern half as observed by rain gauges and collaborated by previous studies (e.g. Hachigonta et al. 2008). This precipitation pattern is a major concern for hydrologists mainly because Lake Kariba, the world’s largest man-made lake by volume and Zambia’s main source of hydroelectricity, is located in the southern part of the country (Libanda et al. 2019). Therefore, the ability of SRPs to pick this precipitation pattern shows that they can among other things, be used for observational and modelling studies that seek to enhance hydrologic impact assessments on hydroelectricity production.

Concluding remarks

The traditional means of rainfall estimation has always been the use of rain gauges. While their advantage of direct precipitation measurements is well documented (Stampoulis et al. 2013), they are often found to be of low density hence of poor spatial resolution. The inherent nature of these point-based gauges inhibits the capturing of the intensity and frequency of precipitation in unmeasured areas. Their uncertainty is also compounded by possible human errors and the effects of wind.

The advent of satellites-based rainfall products (SRPs) has to some extent addressed this problem. However, SRPs are not short of errors and uncertainties. Therefore, they are better used following an extensive validation process (Scofield and Kuligowski 2003; Amitai et al. 2012; Derin et al. 2014; Janjai et al. 2015; Oreggioni et al. 2018). Zambia like many other developing countries is a highly data-scarce country with few and unevenly distributed meteorological stations. To this end, this study set out to investigate the skill of 4 SRPs (i.e. TAMSATv3.0, PERSIANN, CHIRPSv2.0, and ARCv2) in capturing precipitation patterns as observed by 35 rain gauges doted all over Zambia. The goal of the comparative analysis was to examine SRPs’ ability to be used in rain gauge sparse regions of Zambia. Several temporal scales were used for the comparative analysis and they include daily, monthly, seasonal and annual. Investigations were also done on how well SRPs mimic rain gauge data in terms of average, maxima and total precipitation. A comparative analysis of SRPs and gauge data over a multifaceted terrain was also done to investigate their ability to capture rainfall variations over complex topography.

Results indicate that all the 4 SRPs adequately match rain gauge data at monthly scales even on complex topography. Taken together, the coefficient of determination between the individual SRPs and gauge data is generally > 0.9 at monthly scales. However, the ability of these products to capture rain gauge data at daily, seasonal and annual scales differs markedly. Specifically, PERSIANN outperforms all the other SRPs at all scales, CHIRPSv2.0 is rated second, followed by TAMSATv3 and ARCv2, respectively. These results suggest that PERSIANN can be used, reliably, in studies that seek to estimate rainfall in data sparse regions of Zambia. It is however worth noting the differences highlighted in this work and for optimum results, applying calibrations at the local scale.

While this study has shown the suitability of using PERSIANN as a substitute for daily rainfall measurements in Zambia, the enhancement and improvement of meteorological station networks is still imperative. Further, while results embodied in this work are useful for the case of Zambia, they cannot be generalised to other regions. This is because generally, the behaviour of SRPs differs from one region to the other (Zeng et al. 2018).