Introduction

In the aquatic environment, thermal pollution is understood as a result of any process that changes ambient water temperature. In rivers, such change in water temperature that goes beyond the natural range of temperature variation may be caused by discharged heated water coming from different industrial facilities using water for the cooling purpose (thermal electric power plants, chemical plants, etc.). We are aware that relatively small changes in natural ambient temperature might create substantial environmental problems; for instance, they may influence the dissolved oxygen concentration (Rajwa-Kuligiewicz et al. 2015), population of fish and other aquatic organisms and plants (Brett 1956; Coutant 1999; Currie et al. 1998; Murray 2002). The list of potential environmental impacts of thermal pollution is very long and widely discussed in the literature (see, e.g., Caissie 2006; Hester and Doyle 2011; Webb et al. 2008). Therefore, the prediction of possible water temperature increase and assessment of its environmental impact, for example, before constructing industrial facilities become mandatory.

While trying to predict the potential increase of natural water temperature below the heated water discharge, one might have problems with making assumptions and relevant simplifications to obtain a desirable solution. Heat transport models generally consist of nonlinear differential equations with no analytical solutions under real conditions, and therefore, they must be solved numerically. Choosing a proper solution to a problem is a challenge. It requires not only a compromise between the computation time and cost needed to obtain the results and the desired accuracy of the solution but also depends on the availability of input data and their accuracy. The most obvious simplifications of the general three-dimensional (3D) problem pertain to the reduction of the dimension to the two- (2D) or even one-dimensional (1D) problem. That corresponds to the description of so-called near-field (3D); mid-field (2D); or far-field region (1D) (see Table 1). In each, particular region, vertical, horizontal and longitudinal mixing prevails, respectively. While the vertical mixing is relatively fast, the transverse mixing may continue far away from the discharge point. Therefore, the mid-field region is very important from the environmental point of view. To describe the heat transport in the 2D case in the mid-field region, the 2D depth-averaged equation has to be used (see, e.g., Kalinowska and Rowinski 2015; Kalinowska and Rowiński 2008; Rutherford 1994; Szymkiewicz 2010). Further simplifications of heat transport equation are associated with different equation terms. Those terms are often difficult to estimate like, for example, the dispersion tensor components (see, e.g., Kalinowska and Rowiński 2008; Rowinski and Kalinowska 2006) in 2D equation, longitudinal dispersion coefficient (see, e.g., Guymer 1998; Piotrowski et al. 2006; Rowiński et al. 2005; Wallis and Manson 2004) in 1D equation or source functions that may include the information on heat exchange between river water and its surrounding.

Table 1 Schematic description of characteristic regions for mixing in rivers
Full size table

The description of the heat exchange between river water and river surrounding is usually very complicated. The involved processes often depend on various local and temporal factors. It is often taken for granted that the more factors are taken into account in the model/report, the better this model/report is. At the same time, the exact results are expected despite the availability of an insufficient amount of input data. An obvious question arises what result is necessary and what accuracy of the solution is really required. In most cases, modelling of the whole 3D temperature field is not feasible and needed. On the other extreme, we may ask whether 1D models can be sufficient tools for environmental impact assessments for rivers. Usually, it is not the case since vertical mixing takes a lot of time and cross-sectionally averaged temperature values may be much lower than the point values within the cross section. Nevertheless, due to the lack of input data allowing to run 2D models, 1D approaches are often used, but one has to realise that they may introduce serious errors. In case of applying 1D approach, the resulting predicted temperature increase at the beginning (cross-sectionally averaged values) is very low compared to the predicted maximum temperature that may appear at comparable distances from the discharge point in case of 2D approach. The focus of the present paper is, therefore, the modelling of the spread of thermal pollutions in the river mid-field zone, very crucial from the environmental point of view, using the 2D depth-averaged models. For such models within the relatively short timescale (compared to the 1D models), the issue related to the additional heat sources that eventually should be taken into account is of crucial importance. To be very accurate, one may obviously try to include all known possible processes that can potentially affect the river temperature (see, e.g., Evans et al. 1998; Hannah et al. 2004; Johnson 2004; Webb and Zhang 1999; Xin and Kinouchi 2013): heat exchange with the atmosphere and with the river bottom and banks; rainfall and groundwater flow, heat production from biological and chemical processes or friction. However, very often data necessary to calculate those heat fluxes are not easily, if at all, available. For instance, the interactions between riverbed and the stream water are complex and depend on many local and temporal factors like groundwater-stream water flux, shading, bed morphology, geologic heterogeneity. It is difficult to assess them reliably. Most of those heat fluxes usually insignificantly affect the final results in the mid-field zone, especially when we are interested only in temperature difference caused by the artificial heat source (not the actual water temperature itself). Whether their omission is admissible or not strongly depends on the considered case. Note that in some cases, for example, in long timescale or specific situation, some of them may be significant. Generally, in the case of thermal pollution modelling, the issue of omitting different heat exchange terms with the environment such as heat exchange with the bottom, banks and sediment is very common, but the heat exchange with the atmosphere is usually taken into account in various heat transport models and desired by users (even if in 2D models other unavoidable errors committed during the calculation affect the final results to a much larger extent). Often its estimation is very problematic and doubtful, especially in practical applications for thermal pollution spreading. However, the issue of excluding the heat exchange with the atmosphere is usually a subject of discussion. The role of the heat exchange between water and air in case of thermal pollution modelling in rivers in the mid-field region is the main subject of the presented study. This article also summarises existing knowledge on water–air heat exchange calculations, with the special emphasis on practical applications.

Water–air heat exchange

Concerning the heat exchange between a river and its environment, the heat exchange between water and atmosphere is the most significant (Evans et al. 1998; Webb and Zhang 1999). Its intensity depends on water temperature and external meteorological and hydrological conditions, and it is influenced by many processes (Chapra 2008; Edinger 1974; Rutherford et al. 1993) which may be divided into two groups:


Processes independent of water temperature, i.e.,

  • Shortwave solar radiation—radiation emitted by the sun (also called shortwave radiation or solar radiation);

  • Longwave atmospheric radiation—radiation that water receives from the atmosphere (also called thermal radiation); sometimes, it is calculated together with other sources of the longwave radiation from surrounding terrain like, for example, radiation from vegetation;

Processes dependent on water temperature, i.e.,

  • Longwave water back radiation—radiation emitted by the water surface (also called longwave back radiation);

  • evaporation and condensation—there are processes with matter changes from one state to another; evaporation is the loss of water to the atmosphere in the form of water vapour, and it is associated with the heat loss from the water surface, while the condensation is the reverse process;

  • conduction and convection—processes that take place at the border of water and air if they have different temperatures.

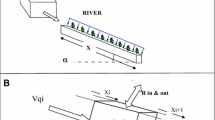
Those processes have been schematically presented in Fig. 1. Note that other processes may also be taken into account but their role usually become significant only in some specific cases.

Fig. 1
figure 1

Most important processes affecting the heat exchange at the water–air interface

Full size image

Finally, the net heat flux QA [W m−2] that results from the energy balance at the water–air interface is defined as follows:

$$Q_{\text{A}} = q_{\text{s}} + q_{\text{a}} - q_{\text{b}} \pm q_{\text{e}} \pm q_{\text{h}} ,$$
(1)

where qs [W m−2]—net flux of shortwave solar radiation, qa [W m−2]—net flux of longwave atmospheric radiation, qb [W m−2]—longwave back radiation flux, qe [W m−2]—evaporation and condensation flux, qh [W m−2]—conduction and convection flux. Many different formulae are available in the literature that can be used to compute each term of Eq. (1), but the selection of an appropriate one is a debatable issue. Generally, the net heat flux is calculated based on the water temperature (Tw) and various meteorological data, primarily on the basis of air temperature (Ta), air humidity (Rh), air pressure (pa), measured shortwave solar radiation (qsi) and wind speed (u) (although many others may be taken into account). Figure 2 presents examples of values of the calculated heat fluxes for a selected case over the day.

Fig. 2
figure 2

Heat fluxes exemplary values calculated for a selected case over the day (Narew River, SET I, Meteo NPN, see Table 3)

Full size image

The practice of calculations of water–air heat exchange

An estimate of the net heat flux at the water–air interface turns out to be a challenge, especially when it has to be based on historical data. The first problem is related to obtaining of necessary input data for the analysed site. Intuitively, the best source in case of meteorological data is the nearest meteorological station. Unfortunately, in many cases, the nearest station does not provide all the necessary data or is still too far from the considered river reach. Another problem is associated with the differences in data obtained from the neighbouring stations. Even in conducive situations when the necessary meteorological data are available in the vicinity of the river reach, we still may receive uncertain results related to the location of the station, for which conditions such as shading or wind speed are often considerably different from those at the river channel. The problem is widely discussed in the literature (see, e.g., Benyahya et al. 2010; Garner et al. 2014; Johnson 2004). Moreover, some measured quantities may vary along the river channel (or even across the river width). Finally, very different values of net heat flux may be obtained. Johnson (2004), for example, measured the heat fluxes for the same stream in case of different conditions. The results showed that the final sum of heat fluxes measured at the same time was 580 W m−2 towards the stream in full sun and 149 W m−2 away from the stream under the shade. Additionally, each term in Eq. (1) is sensitive to the chosen computation method; i.e., different formulae may lead to varying results since they often depend on not well-defined parameters, factors or coefficients that are site specific. Moreover, in the “competition” for the best formula, increasingly “more accurate” formulae take into account more and more factors and thus require more and more input data, which again in practical applications are rarely available or costly.

Study sites and input data

To illustrate the calculations of the net heat flux at the water–air interface and to discuss the possible problems that may be encountered in practical applications, the measured water temperatures in two different lowland rivers in Poland, namely Narew and Świder (see Fig. 3) having different characteristics (see Table 2), were used. Although both river sections are of similar width, Świder River is significantly shallower. The detailed description of both sites may be found in (Rajwa et al. 2014) and (Rajwa-Kuligiewicz et al. 2015). The relevant historical meteorological data necessary to compute the net heat flux QA were collected from different available meteorological stations. Additionally, special in situ measurements on Świder River using the portable meteorological station were performed to execute additional analyses. The station was located on the riverbank to capture the river microclimate conditions.

Fig. 3
figure 3

Map with the marked water temperature measuring points on the Narew (53°04′38″N 22°49′09″E) and Świder (52°06′26″N 21°13′39″E) Rivers (orange and green stars) and selected nearby meteorological stations. Approximate distances [km] from the particular measurement points to meteorological stations have also been indicated. Map has been created with the use of Google Maps

Full size image
Table 2 Considered rivers’ sections characteristics (during the measurement campaign in 2013)
Full size table

All data series mentioned in the paper are listed in Table 3. Water temperature has been measured every 5 or every 1 min. Most of the meteorological data have been measured every minute or more often, for some datasets every 5 min. Thirty-minute backwards averaged values were used for the calculations. Some example sets of meteorological input data used in the article may be found in (Kalinowska et al. 2018, Figs. 1–4). Figure 3 presents the location of measurement points of water temperature in the Narew and Świder Rivers, the nearby meteorological stations providing data and the approximate distance from the measurement points to the considered meteorological stations. Investigations in both rivers were carried out under different conditions, and data from different meteorological stations were taken (for details see Table 3). Some datasets taken into account at the beginning were useless because of existing significant gaps or unexplained outliers, which is sometimes a serious problem in practical applications based on historical data. The discrepancy between data from different stations was also observed (see, e.g., the air temperature and air humidity in Fig. 4). The sensitivity analyses for different input meteorological parameters may be found in Kalinowska et al. (2018).

Table 3 List of input data sets mentioned in the paper
Full size table
Fig. 4
figure 4

Discrepancy that exists between data from different available meteorological stations for Świder River (SET IV): a air temperature; b air humidity

Full size image

Results and discussion

Each term in Eq. (1) was analysed and computed taking into account various calculation methods and different available input data sets for both rivers, preceded by existing knowledge summary. Details of calculations, different options, various empirical or semi-empirical formulae and the problems encountered are discussed below.

Processes independent on water temperature

Shortwave solar radiation

The value of the shortwave solar radiation can vary considerably over time. It depends on many factors such as:

  • sun’s position—varies depending on the date and time of day, site location and elevation above the sea level;

  • scattering and absorption—some amount of solar radiation is absorbed and dissipated by the atmosphere, reflected by clouds or absorbed by atmospheric gases and dust;

  • reflection—upon reaching the water surface, a part of the solar radiation is reflected by the surface;

  • shading—for example, from the riverbank or the riparian vegetation.

The heat flux value may range between 800 and 1000 W m−2 for a sunny day and between 100 and 300 W m−2 for a very cloudy day.

The net flux of shortwave radiation is a result of the difference between incoming (qsi) and reflected solar radiation (qsr) from the water surface, and it is usually approximated by (Magnusson et al. 2012)

$$q_{s} = q_{si} (1 - A),$$
(2)

where A is the albedo (or reflection coefficient for shortwave radiation), [−] is a measure of reflectivity of the water surface. Albedo depends mainly on the colour of the surface (the darker the surface is, the smaller is the albedo), and for water, it ranges from 1 to 10% (depending on the clarity of the water, the water surface conditions—wavelength, chlorophyll concentration, the water depth, etc.). It also depends on the sun angle (water has a higher albedo for low sun angle, Katsaros et al. 1985). In heat budget studies in rivers, its value is usually assumed to be constant and it ranges from 0.02 to 0.07, for example, 0.03 (Benyahya et al. 2010; Caissie et al. 2007); 0.05 (Garner et al. 2014; Magnusson et al. 2012); 0.06 (Xin and Kinouchi 2013); 0.07 (Alcântara et al. 2010). In the present study, the albedo has been assumed to be constant at A = 0.06.

Equation (2) may be additionally corrected, taking into account the shade, by (1 − SF) term, where SF is the shading factor. The SF factor ranges from 0 (no shading) to 1 (complete shading). Many researchers try to consider the influence of the riverbank or riparian vegetation on the net shortwave solar radiation (see, e.g., Garner et al. 2017; Glose et al. 2017; Sinokrot and Stefan 1993), but then additional information about the parameters describing the shading effect is required. Since all those parameters may vary spatially and seasonally, the shading effect is usually not considered in practical applications. It is worth pointing out that not only the density of the vegetation but also the orientation of the channel plays an essential role in controlling solar radiation inputs; refer to Garner et al. (2017), Lee et al. (2012) and Li et al. (2012) for details.

The incoming shortwave radiation qsi may be measured directly by a pyranometer, and in practical applications, the historical data from the nearest meteorological station are usually used. However, as mentioned earlier, the “nearest” meteorological station may by sometimes far away from the measurement site. The example results for the net shortwave solar radiation heat flux qs, calculated based on measured qsi from different meteorological stations for the Narew River (SET I): close to the site (Meteo Choroszcz ~ 12 km, Meteo NPN ~ 2 km) and far away from the site (Meteo IGF UW ~ 159 km, Meteo WAW ~ 168 km), are presented in Fig. 5a. The discrepancy in the results for the close and faraway stations is clearly visible. In the second example for the Świder River (SET IV), the measured values for qsi from three different stations (Meteo Waw ~ 26 km, Meteo IGF UW ~ 25 km and Meteo Szpital Zachodni ~ 42 km) were available. The results of qs (see Fig. 5b) differ between each other but also they differ significantly, especially in the morning, from the qs computed based on the qsi measured directly on site (Meteo Świder Local ~ 0.1 km). This difference may be the effect of the riverbank vegetation. Note that even if we measure the value of qsi on site, it is not without significance whether the station is located on the riverbank, and on which one, or in the middle of the channel.

Fig. 5
figure 5

Net shortwave solar radiation heat flux calculated for: a the Narew River (SET I), based on the measured qsi data from different meteorological stations (Meteo Choroszcz, Meteo NPN, Meteo IGF UW and Meteo WAW), and based on computed theoretical incoming qsi; b the Świder River (SET IV), based on the measured qsi data from different meteorological stations (Meteo Waw, Meteo IGF UW, Meteo Szpital Zachodni, Meteo Świder Local), and based on computed theoretical incoming qsi; c the Świder River (SET III), based on the measured qsi data from Meteo Waw and Meteo Świder Local meteorological stations and based on computed theoretical incoming qsi with and without the inclusion of the correction for cloud cover

Full size image

In case qsi is not measured, it may be estimated for the given geographical location and time of the year and day, using one of the available formulae for the so-called theoretical incoming clear-sky solar radiation, based on the value of the solar constant (see, e.g., Allen et al. 1998; Carmona et al. 2014; Flerchinger et al. 2009; Lhomme et al. 2007). During the calculations, it is crucial not to forget the difference between the local time and solar time (see, e.g., Allen et al. 1998; Khatib and Elmenreich 2015; Lhomme et al. 2007). Otherwise, an unnecessary error may be introduced. Figure 5 presents the results of theoretical qsi calculations for the Narew and Świder rivers for the selected data sets (SET I, SET III and SET IV) (the orange lines). However, such formulae do not include additional effects that reduce the shortwave solar radiation reaching the water surface like, for example, cloud cover. Therefore, a discrepancy between the results based on the theoretically calculated and measured values of qsi is readily seen. It may be huge for cloudy days. Indeed, the discrepancy may be reduced using the formula that includes cloud cover. An example is shown in Fig. 5c (pink line) for the Świder River (SET III). The result is much closer to the result determined based on the measurements from the local meteorological station (black line). However, one has to face the problem of rare availability of the information on cloud cover, and even if it is available, it may be a subject of the judgemental estimate of the observer. Note that cloud cover, also called cloudiness, is the portion of the sky cover that is attributed to clouds and measured in eighths (oktas) or per cents. More exact and devoid of subjunctives is the estimate of cloudiness with use of all-sky cameras.

Consequently, the net shortwave solar radiation values obtained from measured or computed values of qsi may differ significantly. Obviously, the best will be the results based on the value of qsi measured directly on (or close to) the river site. In the case when the meteorological station is far distant from the site, it might be better to use the calculated value of qsi, but only if the cloudiness information is available. In other cases, all received values of the net flux will be very uncertain.

It is worth to note that other methods to estimate hourly solar radiation are also in use, pertaining to machine learning techniques or using a variety of empirical formulae. For example, Khatib and Elmenreich (2015) have proposed a model for predicting hourly solar radiation data using daily solar radiation averages. They have also made an overview of existing empirical formulae.

Longwave atmospheric radiation

The atmosphere as all terrestrial objects emits longwave radiation. The value of atmospheric longwave radiation mostly depends on the air temperature and varies between 30 and 450 W m−2 (Wunderlich 1972). It could be measured directly by pyrgeometer, but while the measurements of shortwave solar radiation are relatively easily available from various meteorological stations, the measurements of longwave atmospheric radiation are unique. For the Narew River analysed case, the nearest meteorological station with such measurements has been found only at a distance of about 159 km away from the measurements site (Meteo IGF UW). The pyrgeometers are also more expensive then pyranometers, and their measurements have usually more significant errors (Choi et al. 2008). The net longwave atmospheric radiation heat flux (qa) is therefore generally calculated using one of the formulae that are based on more readily available measured meteorological data. However, a large number of the proposed formulae for calculation of qa make the choice of the best one very difficult.

All objects with a temperature higher than 0 K emit radiation. The total radiation energy sent by unit of the object surface is proportional to the fourth power of the absolute object temperature. Stefan Boltzmann’s law (Boltzmann 1884) describes this relation:

$$\phi = \varepsilon \sigma T^{4} ,$$
(3)

where ϕ [W m−2]—the heat flux, ε []—the emissivity of the radiating body (ε = 1 for true blackbody), σ = 5.67 × 10−8 [W m−2 K−4]—the Stefan–Boltzmann constant, T [K]—the absolute temperature in kelvin (°C + 273.15).

The incoming longwave atmospheric radiation (qai) reaching the water surface can be determined for the clear-sky conditions using the modified Stefan–Boltzmann law as follows (see, e.g., Chapra 2008; Ji 2008):

$$q_{\text{ai}} = \varepsilon_{\text{a}} \sigma (T_{\text{a}} + 273.15)^{4} .$$
(4)

Then, the net longwave atmospheric radiation is equal to

$$q_{a} = q_{ai} (1 - r),$$
(5)

where εa—emissivity of atmosphere [−], r—reflection coefficient for longwave radiation (for water r = 0.03), Ta [°C]—air temperature [°C].

The biggest problem in applying Eqs. (4) and (5) is how to determine the value of atmospheric emissivity. The first empirical relation was proposed by Ångström (1915). It is usually calculated based on dew point temperature of air (Tang et al. 2004) or most commonly based on measurements of the air temperature and/or the actual vapour pressure (also called water vapour pressure in the air or air vapour pressure) ea [mb = hPa] (see e.g., Anderson 1954; Brunt 1932; Brutsaert 1975; Crawford and Duchon 1999; Idso 1981; Idso and Jackson 1969; Iziomon et al. 2003; Prata 1996; Satterlund 1979; Swinbank 1963), measured close to the water surface (usually two metres above the ground):

$$\varepsilon_{\text{a}} = f(e_{\text{a}} ,T_{\text{a}} ).$$
(6)

Different relationships may be used here: empirical formulae, for example, the formula proposed by Brunt in 1932:

$$\varepsilon_{\text{a}} = a_{1} + a_{2} \sqrt {e_{\text{a}} } ;$$
(7)

or physically based formulae, for example, the Brutsaert formula (1975):

$$\varepsilon_{\text{a}} = a_{3} \left( {\frac{{e_{\text{a}} }}{{T_{\text{a}} + 273.15}}} \right)^{{a_{4} }} ;$$
(8)

where a1[−], a2 [mb−1/2], a3 [mb−a4 K a4] and a4 [−] are empirical coefficients. Originally proposed values by Brant are: a1 = 0.55, a2 = 0.065, and by Brutsaert: a3 = 1.24, a4 = 0.14. The actual vapour pressure may be expressed as:

$$e_{\text{a}} = e_{\text{sat}} \frac{{R_{\text{h}} }}{100},$$
(9)

where Rh—air humidity [%], and esat is a saturation vapour pressure in the air [mb]. The saturation vapour pressure is commonly calculated using the relatively highly accurate empirical Magnus formula (Lawrence 2005; Magnus 1844):

$$e_{\text{sat}} = r_{1} \exp \left( {\frac{{r_{2} T_{\text{a}} }}{{T_{\text{a}} + r_{3} }}} \right),$$
(10)

where r1 [mb], r2 [−], r3 [°C] are empirical coefficients. Two sets of r coefficients are usually used in heat budget studies: 6.12, 17.27 and 237.3 (e.g., Chapra 2008; Raudkivi 1979) and 6.112, 17.67, 243.5 (e.g., Bolton 1980; Ji 2008), but many others had been proposed (refer to Alduchov and Eskridge 1996). However, different sets of r coefficients provide similar results for the considered air temperature values and do not affect the final values of the qa as much as, for example, a1 or a2 coefficients. The second set of coefficients have been used in the paper.

Besides Eqs. (7) and (8), there are many other formulae for atmospheric emissivity calculations. The new methods are usually juxtaposed with oldest formulae, see, for example, Alados et al. (2012), Duarte et al. (2006), Flerchinger et al. (2009), Iziomon et al. (2003), Marthews et al. (2012) and Santos et al. (2011). The selected, used herein, formulae are summarised in Table 4. Note that the coefficients in particular relationships may also take different values and they may vary significantly by site. For example, Table 5 presents the selected values of a1 and a2 coefficients presented in formula (7). Since formula (7) is commonly used in water quality modelling, it has been calibrated for many sites around the world; see, for example, Berdahl and Martin (1984), Berger et al. (1984), FAO (1990), Heitor et al. (1991), Iziomon et al. (2003), Kjaersgaard et al. (2007), Monteith (1961), Sellers (1965), and Swinbank (1963). In summary, according to different studies (Alados et al. 2012; Elsasser 1942; Iziomon et al. 2003; Jiménez et al. 1987), the values for a1 and a2 coefficients range from 0.34 to 0.7 and from 0.023 to 0.110, respectively. Since the clear night-time sky is more emissive than the daytime, some authors, for example, Berdahl and Fromberg (1982) and Li et al. (2017), suggest using different coefficients for the daytime and night-time, or propose a correction depending on the hour of the day (Alados-Arboledas and Jimenez 1988). Above all, it is very important to pay attention to the units in which the vapour pressure is given, and then, correctly convert the values of the coefficients if necessary. It is surprising how many models suffer from simple conversion error.

Table 4 Selected formulae for atmospheric emissivity
Full size table
Table 5 Values of a1 and a2 coefficients in Brunt’s formula (7) for clear-sky atmospheric emissivity used in Figs. 6 and 7
Full size table

Different values may be obtained by applying available formulae for the longwave atmospheric radiation heat flux (see example in Fig. 6). It is worth to point out the difference between results calculated for two different datasets from two metrological stations (close to and far away from the site). Note the difference between the calculated and measured (violet dots) values of longwave atmospheric radiation that was available for one of the considered meteorological stations (Fig. 6b). This difference may be larger or smaller depending on the considered part of the day which is the result of varying sky conditions. In the case of no-clear-sky conditions, the value of atmospheric longwave radiation increases.

Fig. 6
figure 6

Longwave atmospheric radiation heat flux calculated for Narew River (SET I) with different formulae for atmospheric emissivity: a based on data from the nearest meteorological station Meteo NPN (b); based on data from Meteo IGF UW

Full size image

Similarly to the shortwave solar radiation, the mentioned formula for atmospheric emissivity may be corrected, to better predict the longwave atmospheric radiation, by considering the cloud cover. Many correction algorithms have been proposed (see, e.g., summary presented by Flerchinger et al. (2009), and many authors claim that those algorithms improve the results. Since they usually require the information on cloud cover which is rarely available, this makes the calculation even harder. Surprisingly, Abramowitz et al. (2012) showed that such correction factors might be redundant since generally they did not improve the results. They also proposed a new formula for the emissivity of atmosphere for all-sky conditions as follows:

$$\varepsilon_{\text{a}} = a_{5} e_{\text{a}} + a_{6} (T_{\text{a}} + 273.15) - a_{7} ,$$
(11)

which actually in case of the considered data gives the results closer to the measured ones under cloudy sky condition (see Fig. 6b, yellow line). a5, a6 and a7 are empirical coefficients, originally equal to 3.1, 2.84 and 522.5, respectively. A similar formula for all-sky condition (without the necessity to provide information about the cloudiness) based on the Brutsaert formula (8) has been proposed by Sridhar and Elliott (2002). He suggested the value for the a3 coefficients to be equal to 1.31 instead of 1.24 to obtain the better fit to the large range of all cloud condition data. One can see that for the considered case, the Sridhar formula is better than all formulae for clear-sky conditions, but the Abramowitz formula works much better than the formula proposed by Sridhar (Fig. 6b). In cases, when solar radiation measurements are available (which is much more common than the availability of cloudiness information), the problem with cloud cover estimation may be avoided using the solar index defined as:

$$s = \frac{{q_{\text{si}} }}{{q_{{{\text{si}}0}} }},$$
(12)

where qsi is the measured shortwave solar radiation, and qsi0 is the theoretically calculated (estimated) value of the solar radiation for clear-sky condition (see the previous section). Crawford and Duchon (1999) and Lhomme et al. (2007) proposed the formulae for the emissivity of the atmosphere under cloudy sky conditions based on the solar index as follows:

$$\varepsilon_{\text{a}}^{\text{cld}} = (1 - s) + s\varepsilon_{\text{a}}^{{}} ,$$
(13)
$$\varepsilon_{\text{a}}^{\text{cld}} = (1.37 + 0.34s)\varepsilon_{\text{a}}^{{}} ,$$
(14)

where the \(\varepsilon_{\text{a}}^{\text{cld}}\) is the emissivity of the atmosphere under cloudy sky conditions and \(\varepsilon_{\text{a}}^{{}}\) is the emissivity of the atmosphere under clear-sky conditions. Both of them have been applied to correct the results presented in Fig. 6b. As could be seen in Fig. 7 (red line—Crawford and Duchon (1999); blue line—Lhomme et al. (2007)), they improve the results for the cloudy sky conditions during the daytime, but since the information about the solar radiation during the night is not available, they cannot be used to correct the results during the night. In the face of lack of information about the solar index during night-time, Lhomme et al. (2007) proposed to use for the night period, the averaged value of the solar index that appeared between 14:00 and 16:30 the day before. In some studies, an average value for the whole previous day is used. The average values of the solar index, from a day or the end of the day measurements, may help to improve the results. For a particular case, however, with clear-sky conditions during the night (as in the analysed case), the results may be even worse. While using the end of the day measurements of the solar radiation, note that the calculation of the solar index may be troublesome due to the errors of measuring small values of solar radiation. To sum up, when the information about the cloudiness is lacking, the best is to use the all-sky conditions algorithms to calculate the atmospheric emissivity.

Fig. 7
figure 7

Longwave atmospheric radiation heat flux calculated for the Narew River (SET I) with different algorithms for cloudiness correction with the meteorological data from Meteo IGF UW. Formulae for cloudy sky conditions are based on Brutsaert formula (Brutsaert 1975)

Full size image

Additionally to the cloud sky correction, other information, for example, information about site elevation, may be considered (e.g., Deacon 1970; Marks and Dozier 1979), but it insignificantly affects the results (Flerchinger et al. 2009). Also, since all objects emit the longwave radiation, the longwave radiation from topography and vegetation (see, e.g., Leach and Moore 2010) may be taken into account. A detailed review of various relationships based on different input parameters, with various possible corrections, may be found in (Vall and Castell 2017). But it is worth to remember that more corrections and parameters are taken into account, more input data are necessary. Overall, if no measurements for incoming longwave radiation and no additional information are available, the clear-sky or all-sky condition algorithms are the first and the only possible assumption for incoming longwave radiation in practical applications.

Processes dependent on water temperature

Longwave water back radiation

Similarly to all terrestrial objects, water also emits longwave radiation, which can provide a significant contribution to heat loss from the water surface. The value of outgoing water longwave radiation heat flux usually varies from 300 to 500 W m−2 (Deas and Lowney 2000), and assuming that water temperature is known, it is relatively easy to estimate. Similarly to longwave atmospheric radiation, it may also be computed using the Stefan Boltzmann law (see Eq. (3)):

$$q_{b} = \varepsilon_{w} \sigma (T_{w} + 273.15)^{4} ,$$
(15)

where εw—emissivity of water [−]. The water emissivity depends on water transparency and surface smoothness. Often, its value is assumed to be equal to 0.97 (e.g., Chapra 2008; Ji 2008) or to 0.96 (e.g., Brewster 1992), but the values between 0.9 and 0.99 are also applied. Figure 8 shows the range of values that water longwave radiation heat flux can take depending on the assumed water emissivity coefficient for the selected example of the data set (SET III). εw = 0.97 has been used for most calculations performed in the paper.

Fig. 8
figure 8

Range of values (a grey area) that water longwave radiation heat flux can take depending on the assumed water emissivity coefficient (values between 0.9 and 0.99) for selected data set (SET III), and longwave back water radiation heat flux (blue line) calculated for water emissivity coefficient equal to 0.97

Full size image

Evaporation and condensation

Without taking into account the radiation fluxes, the evaporation and condensation heat flux term has the most significant contribution in the total heat budget. However, its value significantly varies among sites and seasons. At the same time, especially within a short time step (like the hourly rate of evaporation), it is difficult to measure evaporation from water in open channels. Commonly accepted methods use the evaporation pan to measure the evaporation rate, but since the hourly evaporation may be of the order of a millimetre or less, very accurate precision is required. Otherwise, the results may become uncertain (Tan et al. 2007). Finally, the evaporation and condensation term in Eq. (1) is usually estimated using one of many indirect methods available in the literature.

Various types of approaches to estimate evaporation are available, for example, radiation-based models, mass or momentum transfer models, temperature-based models and models that used artificial intelligence or mixed-type methods. Comparisons of various approaches may be found, for example, in Ali et al. (2008), Rosenberry et al. (2007), Tan et al. (2007) and Winter et al. (1995). Most of them, however, have been derived or calibrated for long time steps (to estimate daily or monthly evaporation/condensation), and it should be noted that they may not work accurately enough for the hourly time step analysis.

For temperature modelling in open channels and reservoirs, commonly used is the mass transfer approach (see, e.g., Caissie et al. 2007; Sinokrot and Stefan 1993) based on Dalton equation (Dalton 1802). The evaporation is proportional to the difference between the saturation vapour pressure at the water surface—es[mb] and the actual vapour pressure of the air above—ea[mb], and the proportionality factor depends on the value of the wind speed. The heat flux caused by the evaporation and condensation term may be then defined as:

$$q_{\text{e}} = \text{f} \left( u \right)\left( {e_{\text{s}} - e_{\text{a}} } \right) ,$$
(16)

where f(u) [W m−2 mb−1] is so-called wind speed function (or wind function). The saturation vapour pressure at the water surface is equal to:

$$e_{\text{s}} = r_{1} \exp \left( {\frac{{r_{2} T_{\text{w}} }}{{T_{\text{w}} + r_{3} }}} \right) ,$$
(17)

where r1 [mb], r2 [−], r3 [°C] are the same coefficients as in Eq. (10).

The wind speed function is usually a linear or quadratic function of the wind speed and generally may be written as (Ji 2008):

$$\text{f} (u) = b_{0} + b_{1} u + b_{2} u^{2} ,$$
(18)

where b0, b1 and b2 are empirical, usually site-specific coefficients, which may take different values. In practical applications when calibration of the wind speed function is not possible, one of many empirical relations available in the literature has to be chosen. However, it is worth to mention that most of the available formulae have been estimated for lakes or reservoirs and later adapted to rivers and streams. The wind speed function coefficients are sometimes estimated based on the meteorological input data. For example, coefficient b0 (describing the evaporation rate in case of lack of or minimal wind) may be related to the difference between water and air temperature (see, e.g., Arifin et al. 2016; Czernuszenko 1990; Harbeck 1958).

Note that there are different ways to define the heat flux qe. Depending on the definition, in some cases, the wind function must be divided by latent heat of water and water density to be the same as defined by Eqs. (16) and (18). Above all, it is again essential to notice units for f(u) function. Different units may be used for heat flux and vapour pressure which results in different units for f(u) and finally different values of the b0, b1 and b2 coefficients. Similarly to the coefficients in formulae for atmospheric emissivity calculation, also for coefficients in function f(u), we may encounter mistakes derived from simple units calculation errors.

Some researchers, for example (Czernuszenko 1990; Hughes et al. 2011; Trabert 1896), use the relations for wind function that neglect the evaporation in the absence of wind, while others argue that it should also be considered then. Most researchers favour the second opinion. Finally, two forms of the wind formulae are usually met in the literature: linear wind speed function when b2 = 0 (McJannet et al. 2012; Meyer 1928; Ryan 1973) or quadratic one when b1 = 0 (Ahsan and Blumberg 1999; Arifin et al. 2016; Brady et al. 1969; Chapra 2008; Ji 2008). Figure 9 shows how the relations f(u) may look like, including the one proposed by Trabert (1896) using square root relationship: \(\text{f} (u) = 11.25\sqrt u\) (dotted line). The values of the coefficients for other wind speed formulae are summarised in Table 6. The general pattern is that wind increases the evaporation rate, but the value of the proportionality coefficient depends on the chosen formula.

Fig. 9
figure 9

Selected formulae for wind speed function depending on the wind speed value

Full size image
Table 6 Coefficients in the wind speed function empirical formulae used in this paper
Full size table

The impact of the choice of the wind function upon the evaporation and condensation heat flux is presented in Fig. 10. As an example, data set (SET III) for the Świder River has been used, with the input data from the local meteorological station (Fig. 10a), and from the station Meteo Waw (Fig. 10b). The differences are clearly visible. The results are influenced not only by choice of the wind function formula but also by the wind speed value (grey dots). Since the Świder River is sheltered from the wind by the surrounding trees and bushes, the wind speed values measured locally are much lower than the ones observed in the nearby meteorological stations. Consequently, the evaporation heat fluxes for local input data are generally lower. The local values of the wind speed may often be far away from those measured by the nearby meteorological station. Additionally, it is not meaningless at which height above the surface the wind speed is measured. For rivers, it should be measured typically 2 metres above the surface (sometimes 1.5 m), and for lakes and reservoirs, it is usually measured at 7, 8 or 10 metres above the surface. The wind speed generally increases with the height. Although it is possible to recalculate the measured value of the wind speed using log or power wind profile assumption(see, e.g., Allen et al. 1998), this recalculation may be problematic, especially for rivers when measurements are taken far away from the site and for other altitudes. The wind speed values are finally likewise uncertain as wind function coefficients.

Fig. 10
figure 10

Evaporation and condensation heat flux calculated for the Świder River (SET III) with different formulae for wind speed function, based on input data from two different meteorological stations: a local meteorological station—Meteo Świder Local, and bMeteo Waw station

Full size image

According to Winter et al. (1995), errors in the input data may cause serious error in the final evaporation rate value. For example, a few degrees error in measured (or assumed) surface water temperature may cause 40% error in the evaporation rate calculation. In water temperature modelling, usually the depth-averaged values of water temperature (or cross-sectionally averaged values in 1D models) are used and the surface water temperature for sure differs from the depth-averaged values. Although the difference for rivers is usually small, it strongly depends on the local conditions.

To conclude and to obtain accurate results, the best is to calibrate the selected wind speed formula for local conditions using data from local measurements. However, since evaporation measurements are troublesome, and local meteorological data are usually not available, we have to bear in mind that whatever formula we use for calculation of evaporation and condensation heat flux, the results will be very uncertain.

Conduction and convection

Conduction is the process of heat exchange between bodies of different temperatures, which are in direct contact. It consists in transmitting the kinetic energy of the chaotic movement of particles as a result of their collisions.

The process leads to the equalisation of temperature between the bodies. Convection is a process of heat transfer associated with the macroscopic movement of matter. Both processes take place at the border of water and air and can be described using the equation resulting from the Bowen ratio (Bowen 1926; Ji 2008):

$$B = \frac{{q_{\text{h}} }}{{q_{\text{e}} }} = C_{\text{B}} \frac{{p_{\text{a}}^{{}} }}{{p_{0} }}\frac{{T_{\text{w}} - T_{\text{a}} }}{{e_{\text{s}} - e_{\text{a}} }},$$
(19)

where B—Bowen ratio [−], Cb—Bowen coefficient (approximately Cb = 0.62 mb°C−1), p0—reference air pressure (= 1013 mb).

$$q_{\text{h}} = C_{\text{b}} \frac{{p_{\text{a}} }}{{p_{0} }}\text{f} (u)(T_{\text{w}} - T_{\text{a}} ),$$
(20)

Usually, the same wind speed function as for evaporation and condensation heat flux term is used, and the same problems and similar large uncertainty connected with the empirical coefficients and wind speed velocity values apply here. However, the value of the conduction and convection heat flux is usually small compared to the values of other heat fluxes, and its impact on the final results is smaller. Similarly to Fig. 10, Fig. 11 presents the results of computations of the conduction and convection heat flux using different wind function formulae for dataset SET III for the Świder River.

Fig. 11
figure 11

Conduction and convection heat flux calculated for the Świder River (SET III) with different formulae for wind speed function, based on input data from two different meteorological station: a local meteorological station—Meteo Swider Local, and bMeteo Waw station

Full size image

Heat flux with the omission of independent of water temperature terms

The analyses carried out indicate clearly that many factors affect the uncertainty of calculations of heat exchange at the water–air interface, and to obtain the accurate results, many input data are required. In the case of modelling of thermal pollution spreading in rivers, the number of these factors and required input data may be reduced. Since in practical applications we are usually interested in a possible change in natural water temperature caused by artificial heat sources, it is useful to compute the temperature change, ΔTw (difference between actual water temperature and ambient water temperature), instead of the actual water temperature (Tw) itself (see, e.g., Joss and Resele 1987; Kalinowska and Rowinski 2012; Kalinowska et al. 2012). This simplifies the determination of possible heat fluxes resulting from the heat exchange between water and its surrounding environment. All terms that do not depend on water temperature may be omitted during the calculation. They have the same value for different water temperatures and simply counterbalance each other while computing the temperature difference (ΔTw). In the case of heat exchange with the atmosphere, the shortwave solar radiation and longwave atmospheric radiation terms may be disregarded. Although they significantly affect the natural water temperature Tw (causing large daily changes), they do not affect the temperature increase ΔTW caused by external factors, such as the discharges of heated water. The net heat flux (QA) may be then simplified to:

$$Q_{\text{A}} = - q_{\text{b}} \pm q_{\text{e}} \pm q_{\text{h}} .$$
(21)

Finally, while omitting the terms that do not depend on water temperature, acquiring various meteorological input data and problems with the estimation of several factors (e.g., atmospheric emissivity) may be avoided. Unfortunately, the calculation of other factors like the wind speed function will still be problematic. However, in most cases, i.e., while the temperature of the discharged warm water is not very high compared to the temperature of ambient water, it may be assumed that all remaining heat fluxes in Eq. (21) influence both ambient and the warm water similarly. While calculating the water temperature difference, those terms also practically disappear.

For instance, one may calculate the value of the temperature change caused by longwave back water radiation heat flux (which is the most significant water temperature-dependent term at the water–air interface) for natural and heated water temperatures. The temperature of warm water discharged from industrial facilities is usually a few degrees higher than the ambient water temperature. In the mid-field zone, after preliminary vertical mixing, the water temperature is usually not higher than 3 °C. Figure 12 shows the difference (ΔT) between the temperature change for natural water temperature (ΔTw0) and temperate change for heated water temperature—for the assumed 3 °C (ΔTw3) and 7 °C (ΔTw7), respectively—within a half-hour period. Since the value of longwave back water radiation heat flux also depends on the water emissivity coefficient (see, Eq. (15)), additionally, the temperature change for natural water temperature, using different assumed water emissivity coefficients, has been computed. The difference (ΔT) between the temperature change for natural water temperature computed with default emissivity value 0.97 (ΔTw0) and the temperature change for temperature by 3 °C higher than natural water temperature is similar to the difference (ΔT) when we calculate the longwave back water radiation heat flux for natural water temperature with emissivity coefficient equal to 0.93. The difference grows with the water temperature; however, it is of the order of 0.001 °C. For the extreme case (natural water temperature equal to 25 °C) when the ambient water is colder than the heated water by 7 °C, the difference reaches only 0.01 °C.

Fig. 12
figure 12

Difference in temperature change caused by longwave back water radiation when the water temperature is 3 or 7 °C higher than natural water temperature (solid lines) or when different water emissivity coefficients: 0.93 or 0.99 are used (dashed line). Water depth was set to H = 1.8 m, as averaged water depth in case of the Narew River

Full size image

To illustrate the influence of the inclusion of the heat exchange term on the results of thermal pollution modelling in the mid-field zone, the real case study exemplary results have been analysed. The detailed description of the case study may be found in Kalinowska et al. (2012). The River Mixing Model (RivMix), developed by Author, computing the temperature change, has been used (Kalinowska and Rowiński 2008) to predict the water temperature increase caused by heated water discharged from a designed power plant. Two variants of computation have been performed for the examples of chosen (least favoured) conditions. The first variant has been treated with the heat flux caused by water–air heat exchanges included in the calculations (see Fig. 13a), the second one without the heat flux inclusion. After 1 h, the observed difference between the two variants is of the order of 10−2 (see Fig. 13b). Such a difference is relatively small compared to the other sources of errors performed while solving the 2D heat transport equation numerically. For instance, the huge source of uncertainty is the dispersion coefficients estimation. Those coefficients are very difficult to estimate, and therefore, usually different scenarios with various possible values of coefficients are analysed. However, the difference between such scenarios results may be much higher, up to 1 °C (see Kalinowska and Rowinski 2012), compared to the difference obtained with and without the included heat exchange with the atmosphere. Other sources of uncertainty have been analysed in (Kalinowska and Rowinski 2012).

Fig. 13
figure 13

Examples of results for the real case study (see details in Kalinowska et al. 2012). a Predicted temperature increase (ΔT) below the discharge of cooling water from a designed power plant on the Vistula River with the heat flux caused by water–air heat exchange included in the calculations. b The difference in the predicted temperature increase between the results that take into account and results that omit the water–air heat exchange in calculations

Full size image

Conclusions

In the paper, for thermal pollution modelling applications, it is recommended to use models that compute the temperature change instead of the actual river temperature whenever it is possible. Such approach reduces the amount of necessary input data and finally the computation error. In most cases in the mid-field zone, omission of all terms related to heat exchange with the environment including the heat exchange with the atmosphere is recommended. Not perfect input data may in some cases introduce much larger error to the final results than just simple omission of the heat fluxes terms. The problem is especially important in practical cases when we deal with limited and not ideal data. We of course fully realise that in some applications it is necessary to include the heat exchange with the atmosphere and/or other heat fluxes. For example, after full mixing between the heated water and the river water, water temperature change depends only on the heat exchange with the environment. Another example is the heat exchange with the riverbed and banks, which is negligible for most practical applications since it is small compared to the value of heat exchange between the water surface and atmosphere and moreover it is also very uncertain due to its variability and complexity. However, when the source of heated water is located near or on the riverbank, it may turn out to have significant value. Also, most of the possible heat sources will not be significant for large, deep rivers, but much more important for very shallow streams. Since the situation very much depends on the considered case and timescale and space scale, to decide whether 1, 2 or 3D approach is appropriate and which additional heat exchange processes should be taken into account, it is very important to make the proper analyses before calculation or applying of any model. First, the expected outcome together with the appropriate timescale and space scale should be defined. Next, all affecting processes should be analysed subject to their significance and the availability of necessary input data, but also taking into account all other errors that may be committed during the calculations. Since the necessary effort to be taken to provide detailed input data (even the perfect one) for computing the heat exchange with the atmosphere (or environment) is not worth the final outcome in many practical cases (while taking into account other unavoidable committed errors).

In the cases where the heat exchange with the atmosphere estimation is necessary, it is important to bear in mind that its estimation is based on empirical formulae that depend on many uncertain parameters. To be precise, it will be necessary to measure many parameters directly on the side taking into account their space and time dependence to adjust the applied empirical formula to the current conditions. Although such measurements are usually possible for research purpose, in practice, we cannot take advantage of specially planned experiments, whether laboratory or field, allowing to measure a sufficient amount of data. In most cases for various reasons, there are no enough data to perform all the necessary calculations and prediction must be done based on existing historical, often limited and incomplete, sometimes also inaccurate data, as has been shown using two case studies presented in the paper. Therefore, in practical applications, heat exchange with the atmosphere estimation is full of judgements and extremely subjective. The most problematic to estimate is the wind speed function and atmospheric emissivity formulae. The most fragile to local conditions are measured shortwave solar radiation and wind speed value. The analysis and detailed description of particular processes involved in heat exchange with the atmosphere provided in the paper may be useful for practitioners.