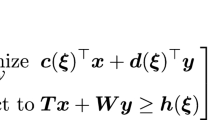Abstract
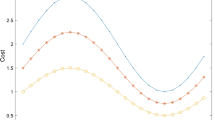
In this paper we introduce a new parameterized Quadratic Decision Rule (QDR), a generalisation of the commonly employed Affine Decision Rule (ADR), for two-stage linear adjustable robust optimization problems with ellipsoidal uncertainty and show that (affinely parameterized) linear adjustable robust optimization problems with QDRs are numerically tractable by presenting exact semi-definite program and second order cone program reformulations. Under these QDRs, we also establish that exact conic program reformulations also hold for two-stage linear ARO problems, containing also adjustable variables in their objective functions. We then show via numerical experiments on lot-sizing problems with uncertain demand that adjustable robust linear optimization problems with QDRs improve upon the ADRs in their performance both in the worst-case sense and after simulated realization of the uncertain demand relative to the true solution.
Similar content being viewed by others
References
Ben-Tal, A., El Ghaoui, L., Nemirovski, A.: Robust Optimization. Princeton Series in Applied Mathematics. Princeton University Press, Princeton, NJ (2009)
Ben-Tal, A., den Hertog, D.: Hidden conic quadratic representation of some nonconvex quadratic optimization problems. Math. Program. 143(1–2, Ser. A), 1–29 (2014)
Ben-Tal, A., Goryashko, A., Guslitzer, E., Nemirovski, A.: Adjustable robust solutions of uncertain linear programs. Math. Program. 99(2, Ser. A), 351–376 (2004)
Ben-Tal, A., Nemirovski, A.: Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications. SIAM, Philadelphia (2001)
Ben-Tal, A., Nemirovski, A.: Robust solutions of uncertain linear programs. Oper. Res. 25, 1–13 (1999)
Ben-Tal, A., Nemirovski, A.: Robust convex optimization. Math Oper. Res. 23(4), 769–805 (1998)
Bertsimas, D., Brown, D.B., Caramanis, C.: Theory and applications of robust optimization. SIAM Rev. 53, 464–501 (2011)
Bertsimas, D., Goyal, V.: On the approximability of adjustable robust convex optimization under uncertainty. Math. Methods Oper. Res. 77(3), 323–343 (2013)
Bertsimas, D., Iancu, D., Parrilo, P.: A hierarchy of near-optimal policies for multi-stage robust adaptive optimization. IEEE Trans. Autom. Control 56, 2809–2824 (2011)
Chuong, T. D., Jeyakumar, V.: A generalized Farkas’ lemma with adjustable variables and two-stage robust linear programs with exact conic dual programs, UNSW Preprint 2019 (submitted for publication)
Chen, A., Zhang, Y.: Uncertain linear programs: extended affinely adjustable robust counterparts. Oper. Res. 57(6), 1469–1482 (2009)
Delage, E., Iancu, D.A.: Robust Multistage Decision Making. INFORMS TutORials in Operations Research, chap. 2, 20–46 (2015)
Goberna, M.A., Jeyakumar, V., Li, G., Vicente-Perez, J.: Robust solutions to multi-objective linear programs with uncertain data. Eur. J. Oper. Res. 242(3), 730–743 (2015)
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx, (March 2014)
Jeyakumar, V., Li, G., Vicente-Perez, J.: Robust SOS-convex polynomial programs: exact SDP relaxations. Optim. Lett. 9(1), 1–18 (2015)
Jeyakumar, V., Li, G.: Exact second-order cone programming relaxations for some nonconvex minimax quadratic optimization problems. SIAM J. Optim. 28, 760–787 (2018)
Marandi, A., den Hertog, D.: When are static and adjustable robust optimization problems with constraint-wise uncertainty equivalent? Math. Program. 170(2), 555–568 (2018)
Xu, G., Hanasusanto, G. A.: Improved decision rule approximations for multi-Stage robust optimization via copositive programming, arXiv:1808.06231 (2018)
Yanikoglu, I., Gorissen, B.L., den Hertog, D.: A survey of adjustable robust optimization. Eur. J. Oper. Res. 277(3), 799–813 (2019)
Zhen, J.: Adjustable Robust Optimization: Theory, Algorithm and Applications. CentER, Center for Economic Research, Tilburg (2018)
Zhen, J., den Hertog, D., Sim, M.: Adjustable robust optimization via Fourier–Motzkin elimination. Oper. Res. 66(4), 1086–1100 (2018)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Woolnough, D., Jeyakumar, V. & Li, G. Exact conic programming reformulations of two-stage adjustable robust linear programs with new quadratic decision rules. Optim Lett 15, 25–44 (2021). https://doi.org/10.1007/s11590-020-01595-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-020-01595-y