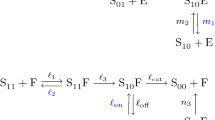Abstract
GTPases are molecular switches that regulate a wide range of cellular processes, such as organelle biogenesis, position, shape, function, vesicular transport between organelles, and signal transduction. These hydrolase enzymes operate by toggling between an active (“ON”) guanosine triphosphate (GTP)-bound state and an inactive (“OFF”) guanosine diphosphate (GDP)-bound state; such a toggle is regulated by GEFs (guanine nucleotide exchange factors) and GAPs (GTPase activating proteins). Here we propose a model for a network motif between monomeric (m) and trimeric (t) GTPases assembled exclusively in eukaryotic cells of multicellular organisms. We develop a system of ordinary differential equations in which these two classes of GTPases are interlinked conditional to their ON/OFF states within a motif through coupling and feedback loops. We provide explicit formulae for the steady states of the system and perform classical local stability analysis to systematically investigate the role of the different connections between the GTPase switches. Interestingly, a coupling of the active mGTPase to the GEF of the tGTPase was sufficient to provide two locally stable states: one where both active/inactive forms of the mGTPase can be interpreted as having low concentrations and the other where both m- and tGTPase have high concentrations. Moreover, when a feedback loop from the GEF of the tGTPase to the GAP of the mGTPase was added to the coupled system, two other locally stable states emerged. In both states the tGTPase is inactivated and active tGTPase concentrations are low. Finally, the addition of a second feedback loop, from the active tGTPase to the GAP of the mGTPase, gives rise to a family of steady states that can be parametrized by a range of inactive tGTPase concentrations. Our findings reveal that the coupling of these two different GTPase motifs can dramatically change their steady-state behaviors and shed light on how such coupling may impact signaling mechanisms in eukaryotic cells.





Similar content being viewed by others
References
Alberts B, Johnson A, Lewis J, Morgan D, Raff M, Roberts K, Walter P (2013) Molecular biology of the cell. 2015. Garland, New York, pp 139–194
Alimohamadi H, Rangamani P (2018) Modeling membrane curvature generation due to membrane-protein interactions. Biomolecules 8(4):120
Alon U (2007) Network motifs: theory and experimental approaches. Nat Rev Genet 8(6):450–461
Alon U (2019) An introduction to systems biology: design principles of biological circuits. CRC Press, Boca Raton
Barr FA, Leyte A, Huttner WB (1992) Trimeric G proteins and vesicle formation. Trends Cell Biol 2(4):91–94
Bhalla US, Iyengar R (1999) Emergent properties of networks of biological signaling pathways. Science 283(5400):381–387
Bhalla US, Iyengar R (2001) Robustness of the bistable behavior of a biological signaling feedback loop. Chaos Interdiscip J Nonlinear Sci 11(1):221–226
Bos JL, Rehmann H, Wittinghofer A (2007) GEFs and GAPs: critical elements in the control of small G proteins. Cell 129(5):865–877
Bourne HR, Sanders DA, McCormick F (1990) The GTPase superfamily: a conserved switch for diverse cell functions. Nature 348(6297):125–132
Bower JM, Bolouri H (2001) Computational modeling of genetic and biochemical networks. MIT Press, Cambridge
Cancino J, Luini A (2013) Signaling circuits on the Golgi complex. Traffic 14(2):121–134
Cardama GA, González N, Maggio J, Menna PL, Gomez DE (2017) RhoGTPases as therapeutic targets in cancer. Int J Oncol 51(4):1025–1034
Changeux J-P, Thiéry J, Tung Y, Kittel C (1967) On the cooperativity of biological membranes. Proc Natl Acad Sci USA 57(2):335
Chantalat S, Courbeyrette R, Senic-Matuglia F, Jackson CL, Goud B, Peyroche A (2003) A novel Golgi membrane protein is a partner of the ARF exchange factors Gea1p and Gea2p. Mol Biol Cell 14(6):2357–2371
Cherfils J, Zeghouf M (2013) Regulation of small GTPases by GEFs, GAPs, and GDIs. Physiol Rev 93(1):269–309
Cowan AE, Moraru II, Schaff JC, Slepchenko BM, Loew LM (2012) Spatial modeling of cell signaling networks, In: Methods in cell biology, vol. 110, pp. 195–221, Elsevier
DiGiacomo V, Maziarz M, Luebbers A, Norris JM, Laksono P, Garcia-Marcos M (2020) Probing the mutational landscape of regulators of G protein signaling proteins in cancer. Sci Signal 13(617)
Donaldson JG, Honda A, Weigert R (2005) Multiple activities for Arf1 at the Golgi complex. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1744(3):364–373
Etienne-Manneville S, Hall A (2002) RhoGTPases in cell biology. Nature 420(6916):629–635
Eungdamrong NJ, Iyengar R (2004) Modeling cell signaling networks. Biol Cell 96(5):355–362
Evers E, Zondag G, Malliri A, Price L, Ten Klooster J-P, Van Der Kammen R, Collard J (2000) Rho family proteins in cell adhesion and cell migration. Eur J Cancer 36(10):1269–1274
Famili I, Palsson BO (2003) The convex basis of the left null space of the stoichiometric matrix leads to the definition of metabolically meaningful pools. Biophys J 85(1):16–26
Ferrell JE Jr (2002) Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr Opin Cell Biol 14(2):140–148
Ferrell JE Jr, Xiong W (2001) Bistability in cell signaling: How to make continuous processes discontinuous, and reversible processes irreversible. Chaos Interdiscip J Nonlinear Sci 11(1):227–236
Finley SD, Popel AS (2013) Effect of tumor microenvironment on tumor VEGF during anti-VEGF treatment: systems biology predictions. JNCI J Natl Cancer Inst 105(11):802–811
Finley SD, Broadbelt LJ, Hatzimanikatis V (2009) Computational framework for predictive biodegradation. Biotechnol Bioeng 104(6):1086–1097
Garcia-Marcos M, Ghosh P, Farquhar MG (2009) GIV is a nonreceptor gef for G\(\alpha \)i with a unique motif that regulates Akt signaling. Proc Natl Acad Sci 106(9):3178–3183
Getz M, Swanson L, Sahoo D, Ghosh P, Rangamani P (2019) A predictive computational model reveals that GIV/girdin serves as a tunable valve for EGFR-stimulated cyclic AMP signals. Mol Biol Cell 30(13):1621–1633
Ghosh P (2015) Heterotrimeric G proteins as emerging targets for network based therapy in cancer: end of a long futile campaign striking heads of a Hydra. Aging (Albany NY) 7(7):469
Ghosh P, Rangamani P, Kufareva I (2017) The GAPs, GEFs, GDIs and- now, GEMs: new kids on the heterotrimeric G protein signaling block. Cell Cycle 16(7):607–612
Ghusinga KR, Jones RD, Jones AM, Elston TC (2020) Molecular switch architecture drives response properties, bioRxiv
Gillespie DT (2009) Deterministic limit of stochastic chemical kinetics. J Phys Chem B 113(6):1640–1644
Gilman AG (1987) G proteins: transducers of receptor-generated signals. Annu Rev Biochem 56(1):615–649
Goldbeter A, Koshland DE (1981) An amplified sensitivity arising from covalent modification in biological systems. Proc Natl Acad Sci 78(11):6840–6844
Hahl SK, Kremling A (2016) A comparison of deterministic and stochastic modeling approaches for biochemical reaction systems: on fixed points, means, and modes. Front Genet 7:157
Hamm HE (1998) The many faces of G protein signaling. J Biol Chem 273(2):669–672
Hanahan D, Weinberg RA (2000) The hallmarks of cancer. Cell 100(1):57–70
Hartung A, Ordelheide A-M, Staiger H, Melzer M, Häring H-U, Lammers R (2013) The Akt substrate Girdin is a regulator of insulin signaling in myoblast cells. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1833(12):2803–2811
Hassinger JE, Oster G, Drubin DG, Rangamani P (2017) Design principles for robust vesiculation in clathrin-mediated endocytosis. Proc Natl Acad Sci 114(7):E1118–E1127
Hooshangi S, Thiberge S, Weiss R (2005) Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc Natl Acad Sci 102(10):3581–3586
Hornung G, Barkai N (2008) Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. PLoS Comput Biol 4(1):e8
Ingolia NT, Murray AW (2007) Positive-feedback loops as a flexible biological module. Curr Biol 17(8):668–677
Jamora C, Takizawa PA, Zaarour RF, Denesvre C, Faulkner DJ, Malhotra V (1997) Regulation of Golgi structure through heterotrimeric G proteins. Cell 91(5):617–626
Lipshtat A, Jayaraman G, He JC, Iyengar R (2010) Design of versatile biochemical switches that respond to amplitude, duration, and spatial cues. Proc Natl Acad Sci 107(3):1247–1252
Liu WN, Yan M, Chan AM (2017) A thirty-year quest for a role of R-Ras in cancer: from an oncogene to a multitasking gtpase. Cancer Lett 403:59–65
Lo I-C, Gupta V, Midde KK, Taupin V, Lopez-Sanchez I, Kufareva I, Abagyan R, Randazzo PA, Farquhar MG, Ghosh P (2015) Activation of G\(\alpha \)i at the Golgi by GIV/Girdin imposes finiteness in Arf1 signaling. Dev Cell 33(2):189–203
Logsdon EA, Finley SD, Popel AS, Gabhann FM (2014) A systems biology view of blood vessel growth and remodelling. J Cell Mol Med 18(8):1491–1508
Lopez-Sanchez I, Dunkel Y, Roh Y-S, Mittal Y, De Minicis S, Muranyi A, Singh S, Shanmugam K, Aroonsakool N, Murray F et al (2014) GIV/Girdin is a central hub for profibrogenic signalling networks during liver fibrosis. Nat Commun 5(1):1–18
Ma GS, Aznar N, Kalogriopoulos N, Midde KK, Lopez-Sanchez I, Sato E, Dunkel Y, Gallo RL, Ghosh P (2015) Therapeutic effects of cell-permeant peptides that activate G proteins downstream of growth factors. Proc Natl Acad Sci 112(20):E2602–E2610
Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002) Network motifs: simple building blocks of complex networks. Science 298(5594):824–827
Morris MK, Saez-Rodriguez J, Sorger PK, Lauffenburger DA (2010) Logic-based models for the analysis of cell signaling networks. Biochemistry 49(15):3216–3224
Neves SR, Ram PT, Iyengar RG (2002) Protein pathways. Science 296(5573):1636
Nusse HE, Yorke JA (2012) Dynamics: numerical explorations: accompanying computer program dynamics, vol 101. Springer, Berlin
O’hayre M, Vázquez-Prado J, Kufareva I, Stawiski EW, Handel TM, Seshagiri S, Gutkind JS (2013) The emerging mutational landscape of G proteins and G-protein-coupled receptors in cancer. Nat Rev Cancer 13(6):412–424
Papasergi MM, Patel BR, Tall GG (2015) The G protein \(\alpha \) chaperone Ric-8 as a potential therapeutic target. Mol Pharmacol 87(1):52–63
Pedraza JM, van Oudenaarden A (2005) Noise propagation in gene networks. Science 307(5717):1965–1969
Perko L (2013) Differential equations and dynamical systems, vol 7. Springer, Berlin
Qiao L, Zhao W, Tang C, Nie Q, Zhang L (2019) Network topologies that can achieve dual function of adaptation and noise attenuation. Cell Syst 9(3):271–285
Rangamani P, Sirovich L (2007) Survival and apoptotic pathways initiated by TNF-\(\alpha \): modeling and predictions. Biotechnol Bioeng 97(5):1216–1229
Rein U, Andag U, Duden R, Schmitt HD, Spang A (2002) ARF-GAP-mediated interaction between the ER-golgi v-SNAREs and the COPI coat. J Cell Biol 157(3):395–404
Rossman KL, Der CJ, Sondek J (2005) GEF means go: turning on RhoGTPases with guanine nucleotide-exchange factors. Nat Rev Mol Cell Biol 6(2):167–180
Shen-Orr SS, Milo R, Mangan S, Alon U (2002) Network motifs in the transcriptional regulation network of escherichia coli. Nat Genet 31(1):64–68
Shibata T, Fujimoto K (2005) Noisy signal amplification in ultrasensitive signal transduction. Proc Natl Acad Sci 102(2):331–336
Siderovski DP, Willard FS (2005) The GAPs, GEFs, and GDIs of heterotrimeric G-protein alpha subunits. Int J Biol Sci 1(2):51
Sriram K, Moyung K, Corriden R, Carter H, Insel PA (2019) GPCRs show widespread differential mrna expression and frequent mutation and copy number variation in solid tumors. PLoS Biol 17(11):e3000434
Stow J (1995) Regulation of vesicle trafficking by G proteins. Curr Opin Nephrol Hypertens 4:421–425
Stow JL, Heimann K (1998) Vesicle budding on Golgi membranes: regulation by G proteins and myosin motors. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1404(1–2):161–171
Stow JL, De Almeida JB, Narula N, Holtzman EJ, Ercolani L, Ausiello DA (1991) A heterotrimeric G protein, G alpha i–3, on Golgi membranes regulates the secretion of a heparan sulfate proteoglycan in LLC-PK1 epithelial cells. J Cell Biol 114(6):1113–1124
Strogatz SH (1994) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry and engineering, 1st edn. Westview Press, Boulder
Takai Y, Sasaki T, Matozaki T (2001) Small GTP-binding proteins. Physiol Rev 81(1):153–208
Wang J, Tu Y, Mukhopadhyay S, Chidiac P, Biddlecome GH, Ross EM (1999) GTPase-activating proteins (GAPs) for heterotrimeric G proteins. G Proteins Tech Anal 123–151
Wang H, Misaki T, Taupin V, Eguchi A, Ghosh P, Farquhar MG (2015) GIV/girdin links vascular endothelial growth factor signaling to akt survival signaling in podocytes independent of nephrin. J Am Soc Nephrol 26(2):314–327
Wu V, Yeerna H, Nohata N, Chiou J, Harismendy O, Raimondi F, Inoue A, Russell RB, Tamayo P, Gutkind JS (2019) Illuminating the Onco-GPCRome: Novel G protein-coupled receptor-driven oncocrine networks and targets for cancer immunotherapy. J Biol Chem 294(29):11062–11086
Yen P, Finley SD, Engel-Stefanini MO, Popel AS (2011) A two-compartment model of VEGF distribution in the mouse. PLoS ONE 6(11):e27514
Acknowledgements
This work was supported by Air Force Office of Scientific Research (AFOSR) Multidisciplinary University Research Initiative (MURI) Grant FA9550-18-1-0051 (to P. Rangamani) and the National Institute of Health (CA100768, CA238042 and AI141630 to P. Ghosh). Lucas M. Stolerman acknowledges support from the National Institute of Health (CA209891). The authors would like to acknowledge Prof. Ali Behzadan (Sacramento State University) for his careful reading and insightful comments for this work.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Proof of Proposition 3.1
We must find nonnegative \(\widehat{[mG]}\), \(\widehat{[mG^*]}\), \(\widehat{{\mathcal {G}}^*}\), and \(\widehat{{\mathcal {T}}^*}\) satisfying the following system:
From Eq. A.3, we must have \(\widehat{[mG^*]}=0\) or \(\widehat{{\mathcal {G}}^*} = 1 \). Thus, we divide the steady-state analysis in two cases.
\(\underline{\hbox {Case 1: }\widehat{[mG^*]}=0.}\)
From Eq. A.1, we must have \(\widehat{[mG]}=0\), and from Eq. A.4, we obtain \( \widehat{\mathcal {G^*}} = \frac{C}{[tGEF_{tot}]} \). Since \(\widehat{\mathcal {G^*}} \le 1 \) by definition, we conclude that
Equation A.5 is also sufficient for \(\widehat{[mG^*]}=0\). Otherwise, if \(C \le [tGEF_{tot}]\) and \(\widehat{[mG^*]}>0\), then \(\widehat{\mathcal {G^*}} = 1\) (Eq. A.3) and from Eq. A.4, we would conclude that \(\widehat{[mG]}+\widehat{[mG^*]} \le 0\), which is impossible.
Finally, by substituting \( \widehat{\mathcal {G^*}}\) in Eq. A.2, we obtain \(\widehat{{\mathcal {T}}^*} = \frac{1}{1+\frac{\rho ^{tG}_{off}}{\rho ^{tG}_{on} C}}\), and therefore, the steady state is given by
\(\underline{\hbox {Case 2: }\widehat{\mathcal {G^*}}=1}\)
In this case, \( \widehat{[mG^*]} \ge 0\) and from Eqs. A.1 and A.4, we obtain
and
In this case, since the steady state has to be nonnegative, we must have
which is also sufficient for \(\widehat{\mathcal {G^*}}=1\). Otherwise if \(C \ge [tGEF_{tot}]\) and \(\widehat{\mathcal {G^*}}<1\), then \(\widehat{[mG^*]}=\widehat{[mG]}=0\) (Eqs. A.1 and A.3), and from Eq. A.4, we would have
which is impossible.
Finally, by substituting \(\widehat{\mathcal {G^*}}=1\) in Eq. A.2, we obtain
which gives \(\widehat{{\mathcal {T}}^*} = \frac{\rho ^{tG}_{on} [tGEF_{tot}]}{\rho ^{tG}_{on}[tGEF_{tot}] + \rho ^{tG}_{off}}\) and therefore
Appendix B. Proof of Theorem 3.2
We begin our proof by computing the steady states of the system, which are solutions of the algebraic system given by Eqs. 3.27–3.32. We also establish necessary and sufficient conditions involving the parameters \(C_1\), \(C_2\), and \([mGAP_{tot}]\) for the existence of each steady state. We then compute the Jacobian matrix of the system and determine the local stability of the steady state based on the classical linearization procedure (Strogatz 1994).
1.1 Steady States
We divide our analysis into four different cases that emerge from the preliminary inspection of the system given by Eqs. 3.27–3.32.
\(\underline{\hbox {Case 1: }\widehat{[mG^*]}=0\hbox { and }\widehat{[mGAP^*]}=[mGAP_{tot}].}\)
From Eq. 3.27, we have \(\widehat{[mG]} = 0\) and from Eq. 3.31, \(\widehat{[tGEF^*]} = C_1 - [mGAP_{tot}]\). Thus, \(C_1 \ge [mGAP_{tot}]\) since the steady state must be nonnegative. Now Eq. 3.32 gives \(\widehat{[tGEF]} = C_2 - C_1\) and that implies \(C_2 \ge C_1\).
Finally, Eq. 3.28 yields
and hence,
The steady state is therefore given by
We now observe that the two parameter relations
are sufficient for \(\widehat{[mG^*]}=0\) and \(\widehat{[mGAP^*]}=[mGAP_{tot}]\). First, we observe that if \(C_2 \ge C_1\) then \(\widehat{[mG^*]}=0\). In fact, by subtracting Eq. 3.31 from Eq. 3.32, we obtain
and hence, \( \widehat{[tGEF]} \ge \widehat{[mG]} + \widehat{[mG^*]} \). On the other hand, from Eq. 3.29, we must have \( \widehat{[tGEF]}=0\) or \(\widehat{[mG^*]}=0\). Thus, if \( \widehat{[tGEF]}=0\) then \(\widehat{[mG]} + \widehat{[mG^*]} \le 0\), and hence, the nonnegativeness of the steady state implies \(\widehat{[mG]}=\widehat{[mG^*]}=0\). Now, Eq. 3.31 gives \(\widehat{[tGEF^*]} = C_1 - \widehat{[mGAP^*]}\) and from Eq. 3.30, we must have \(\widehat{[mGAP^*]}= [mGAP_{tot}]\) or \(\widehat{[tGEF^*]}=0\). If \(\widehat{[tGEF^*]}=0\), then \(\widehat{[mGAP^*]} = C_1 \ge [mGAP_{tot}]\), and hence, \(\widehat{[mGAP^*]} = [mGAP_{tot}]\). Therefore, we have shown that Eq. B.1 imply \(\widehat{[mG^*]}=0\) and \(\widehat{[mGAP^*]}=[mGAP_{tot}]\). Consequently, the steady state in this case must be given by Eq. 3.33.
\(\underline{\hbox {Case 2: } \widehat{[tGEF]}=0\hbox { and }\widehat{[mGAP^*]}=[mGAP_{tot}]}\)
From Eq. 3.32, \(\widehat{[tGEF^*]} = C_2 - [mGAP_{tot}] \), and hence, \([mGAP_{tot}] \le C_2\). From Eq. 3.31, we must have \( \widehat{[mG]} + \widehat{[mG^*]} = C_1 - C_2\) and that implies \(C_1 \ge C_2\). Now, Eq. 3.27 gives
and therefore
From Eq. 3.28, we must have
from which we obtain
and therefore, the steady state is given by
We now observe that the two parameter relations
are sufficient for \( \widehat{[tGEF]}=0\) and \(\widehat{[mGAP^*]}=[mGAP_{tot}]\).
In fact, if \(C_1 \ge C_2\) then \(\widehat{[tGEF]}=0\) from the same argument as in Case 1. Now, Eq. 3.32 gives \(\widehat{[tGEF^*]} = C_2 - \widehat{[mGAP^*]}\) and from Eq. 3.30, we must have \( \widehat{[mGAP^*]} = [mGAP_{tot}]\) or \(\widehat{[tGEF^*]}=0\). If \(\widehat{[tGEF^*]}=0\), then \( \widehat{[mGAP^*]} = C_2 \ge [mGAP_{tot}]\) (from Eq. B.2), and thus, \(\widehat{[mGAP^*]} = [mGAP_{tot}]\). Therefore, we have shown that Eq. B.2 imply \( \widehat{[tGEF]}=0\) and \(\widehat{[mGAP^*]}=[mGAP_{tot}]\). Consequently, the steady state in this case must be given by Eq. 3.34.
\(\underline{\hbox {Case 3: }\widehat{[mG^*]}=0 and \widehat{[tGEF^*]}=0.}\)
From Eq. 3.27, we have \(\widehat{[mG]} = 0\) and from Eq. 3.28, we also get \(\widehat{{\mathcal {T}}^*} =0\) since \(\rho ^{tG}_{off}>0\). Now, Eq. 3.31 gives \(\widehat{[mGAP^*]} = C_1\), and thus, we must have \(C_1 \le [mGAP_{tot}]\). Moreover, Eq. 3.32 results in \(\widehat{[tGEF]} = C_2 - C_1\) and since all steady states must be nonnegative, we obtain \(C_2 \ge C_1\). In this case, the steady state is given by
We now observe that the two parameter relations
are sufficient for \(\widehat{[mG^*]}=0\) and \(\widehat{[tGEF^*]}=0\). In fact, \(C_2 \ge C_1\) implies \(\widehat{[mG^*]}=0\) from the same argument as in Case 1.
Now, Eq. 3.31 gives \(\widehat{[tGEF^*]} = C_1 - \widehat{[mGAP^*]}\) and from Eq. 3.30, we must have \(\widehat{[tGEF^*]}=0\) or \(\widehat{[mGAP^*]}= [mGAP_{tot}]\). If \(\widehat{[mGAP^*]}=[mGAP_{tot}]\), then \(\widehat{[tGEF^*]} = C_1 - [mGAP_{tot}] \le 0\) (from Eq. B.4), and thus, \(\widehat{[tGEF^*]} = 0\). Therefore, we have shown that Eq. B.4 imply \(\widehat{[mG^*]}=0\) and \(\widehat{[tGEF^*]} = 0\). Consequently, the steady state in this case must be given by Eq. 3.35.
\(\underline{\hbox {Case 4: } \widehat{[tGEF]}=0\hbox { and } \widehat{[tGEF^*]} = 0 }\)
From Eq. 3.32, we obtain \(\widehat{[mGAP^*]}=C_2\), and hence, \(C_2 \le [mGAP_{tot}]\). From Eq. 3.31, we have \(\widehat{[mG]} + \widehat{[mG^*]} = C_1 - C_2\) and that implies \(C_1 \ge C_2\) since the concentrations at steady state must be nonnegative. Eq. 3.27 then gives
from which we obtain
From Eq. 3.28, we have \(\widehat{{\mathcal {T}}^*} = 0\), and therefore, the steady state is given by
We now observe that the two parameter relations
are sufficient for \( \widehat{[tGEF]}=0\) and \(\widehat{[tGEF^*]} = 0\). In fact, if \(C_1 \ge C_2\) then by subtracting Eq. 3.32 from Eq. 3.31, we have
and hence, \( \widehat{[mG]} + \widehat{[mG^*]} \ge \widehat{[tGEF]} \). On the other hand, from Eq. 3.29, we must have \( \widehat{[tGEF]}=0\) or \(\widehat{[mG^*]}=0\). Thus, if \(\widehat{[mG^*]} = 0\) then \(\widehat{[mG]} = 0\) (from Eq. 3.27), and hence, the nonnegativeness implies \(\widehat{[tGEF]}=0\). Hence, we conclude that Eq. B.5 guarantee \(\widehat{[tGEF]}=0\).
Now, Eq. 3.32 gives \(\widehat{[tGEF^*]} = C_2 - \widehat{[mGAP^*]}\) and from Eq. 3.30, we must have \(\left( [mGAP_{tot}] - \widehat{[mGAP^*]} \right) =0\) or \(\widehat{[tGEF^*]}=0\). If \(\widehat{[mGAP^*]}=[mGAP_{tot}]\) then \(\widehat{[tGEF^*]} = C_2 - [mGAP_{tot}] \le 0\) (from Eq. B.5), and thus, \(\widehat{[tGEF^*]} = 0\). Therefore, we have shown that Eq. B.5 implies \(\widehat{[tGEF]}=0\) and \(\widehat{[tGEF^*]} = 0\). Consequently, the steady state in this case must be given by Eq. 3.36.
1.2 Local Stability Analysis
We begin reducing the ODE system with the conservation laws given by Eqs. 3.19 and 3.20. In fact, if we write
then Eqs. 3.21–3.26 can be written in the form
where
and
The eigenvalues of the Jacobian matrix can be thus calculated for each one of the four steady states given by Eqs. 3.33–3.36. We prove that all steady states are LAS by showing that the eigenvalues of the Jacobian matrix are all negative real numbers. We perform the calculations with MATLAB’s R2019b symbolic toolbox and analyze each case separately (see supplementary file with MATLAB codes). We analyze each case separately.
-
(1)
If \(C_1 > [mGAP_{tot}]\) and \(C_2>C_1\), the Jacobian matrix evaluated at the steady state given by Eq. 3.33 gives the eigenvalues
$$\begin{aligned} \lambda _1 = -\rho ^{mG}_{on}(C_1 - [mGAP_{tot}]) \quad \text {and} \quad \lambda _2 = - \rho ^{tG}_{on} ( C_1 - [mGAP_{tot}] ) - \rho ^{tG}_{off} \end{aligned}$$which are negative. Moreover, the other eigenvalues \(\lambda _3\) and \(\lambda _4\) are such that
$$\begin{aligned} \lambda _3 + \lambda _4 = \rho ^{I}_{on} (C_1 - C_2) - 1 - \rho ^{mG}_{off} [mGAP_{tot}] < 0 \end{aligned}$$and
$$\begin{aligned} \lambda _3 \lambda _4 = - \rho ^{I}_{on}(C_1 - C_2) >0, \end{aligned}$$and thus, \(\lambda _3\) and \(\lambda _4\) are negative, and hence, the steady state is LAS.
-
(2)
If \(C_2 > [mGAP_{tot}]\) and \(C_1>C_2\), the Jacobian matrix evaluated at the steady state given by Eq. 3.34 gives the eigenvalues
$$\begin{aligned} \lambda _1= & {} - \rho ^{tG}_{off} - \rho ^{tG}_{on} (C_2 - [mGAP_{tot}]), \quad \lambda _2 = - 1 - \rho ^{mG}_{off}[mGAP_{tot}],\\ \lambda _3= & {} -\rho ^{II}_{on} (C_2 - [mGAP_{tot}]) \quad \text {and} \quad \lambda _4 = -\frac{\rho ^{I}_{on} (C_1 - C_2)}{\rho ^{mG}_{off} [mGAP_{tot}] + 1} \end{aligned}$$which are all negative, and hence, the steady state is LAS.
-
(3)
If \(C_1 < [mGAP_{tot}]\) and \(C_2>C_1\),the Jacobian matrix evaluated at the steady state given by Eq. 3.35 gives the eigenvalues
$$\begin{aligned} \lambda _1 = \rho ^{II}_{on} (C_1 - [mGAP_{tot}]) \quad \text {and} \quad \lambda _2 = -\rho ^{tG}_{off} \end{aligned}$$which are negative. Moreover, the other eigenvalues \(\lambda _3\) and \(\lambda _4\) are such that
$$\begin{aligned} \lambda _3 + \lambda _4 = \rho ^{I}_{on}(C_1 -C_2) - C_1 \rho ^{mG}_{off} - 1 < 0 \end{aligned}$$and
$$\begin{aligned} \lambda _3 \lambda _4 = -\rho ^{I}_{on}(C_1 - C_2)>0, \end{aligned}$$and thus, \(\lambda _3\) and \(\lambda _4\) are negative, and hence, the steady state is LAS.
-
(4)
If \(C_2 < [mGAP_{tot}]\) and \(C_1 > C_2\), the Jacobian matrix evaluated at the steady state given by Eq. 3.36 gives the eigenvalues
$$\begin{aligned} \lambda _1 = - 1 - C_2 \rho ^{mG}_{off} , \quad \lambda _2 = \rho ^{II}_{on} (C_2 - [mGAP_{tot}]), \quad \lambda _3 = -\rho ^{tG}_{off} \end{aligned}$$and
$$\begin{aligned} \lambda _4 = -\frac{\rho ^{I}_{on}(C_1 - C_2)}{C_2 \rho ^{mG}_{off} + 1} \end{aligned}$$which are all negative, and hence, the steady state is LAS.
Appendix C. Proof of Theorem 3.3
We proceed with the steady-state analysis in the same way of Theorem 3.2. We consider the same four different cases and calculate the \(\xi \)-dependent families of steady states, where \(\xi \ge 0\) represents the tG concentration. We also obtain necessary relationships for the conserved quantities \(\tilde{C_2}\), \(\tilde{C_1}\), and \([mGAP_{tot}]\), as well as admissible intervals for \(\xi \) that guarantee the existence of nonnegative steady states.
\(\underline{\hbox {Case 1: }\widehat{[mG^*]}=0\hbox { and }\widehat{[mGAP^*]}=[mGAP_{tot}]}\).
From Eq. 3.39, we have \(\widehat{[mG]}=0\) and subtracting Eq. 3.38 from Eq. 3.37, we get \(\widehat{[tGEF]} = \tilde{C_2} - \tilde{C_1} \ge 0\) only if \(\tilde{C_2} \ge \tilde{C_1} \). Substituting \(\widehat{[tGEF]}\) on the conservation law given by Eq. 3.38 and using Eq. 3.40 to write \(\widehat{[tG^*]} = \frac{\rho ^{tG}_{on}\widehat{[tGEF^*]} \xi }{\rho ^{tG}_{off}},\) we obtain
and hence,
only if \(\tilde{C_1} - [mGAP_{tot}] \ge \xi . \) Therefore, in this case the \(\xi \)-dependent family of steady states is given by
\(\underline{\hbox {Case 2: } \widehat{[tGEF]}=0\hbox { and }\widehat{[mGAP^*]}=[mGAP_{tot}]}\)
Using Eq. 3.39 to write \(\widehat{[mG]} = \rho ^{mG}_{off} [mGAP_{tot}] \widehat{[mG^*]}\) and subtracting Eq. 3.38 from Eq. 3.37, we obtain the expressions for \([mG^*]\) and [mG]
and thus, we must have \(\tilde{C_1} \ge \tilde{C_2}\). Now looking at Eq. 3.38 and substituting \(\widehat{[tG^*]} = \frac{\rho ^{tG}_{on}\widehat{[tGEF^*]} \xi }{\rho ^{tG}_{off}}\) from Eq. 3.40, we obtain
only if \(\tilde{C_2} - [mGAP_{tot}] \ge \xi \). Therefore, in this case the \(\xi \)-dependent family of steady states is given by
\(\underline{\hbox {Case 3: }\widehat{[mG^*]}=0\hbox { and }\widehat{[tGEF^*]}=0}\)
From Eqs. 3.39 and 3.40, we have \(\widehat{[mG]}=0\) and \(\widehat{[tG^*]}=0\), respectively. Subtracting Eq. 3.38 from Eq. 3.37, in this case we get \(\widehat{[tGEF]} = \tilde{C_2} - \tilde{C_1} \ge 0\) only if \(\tilde{C_2} \ge \tilde{C_1} \). Now, from the conservation law given by Eq. 3.37, we obtain \(\widehat{[mGAP^*]} = \tilde{C_1} - \xi \), and thus, \(\widehat{[mGAP^*]} \in [0,[mGAP_{tot}]]\) only if \(\max (0,\tilde{C_1} - [mGAP_{tot}]) \le \xi \le \tilde{C_1}\). In this case, the \(\xi \)-dependent family of steady states is given by
\(\underline{\hbox {Case 4: }\widehat{[tGEF]}=0\hbox { and }\widehat{[tGEF^*]} = 0}\)
Equation 3.40 gives \(\widehat{[tG^*]}=0\) and the conservation law given by Eq. 3.38 yields \(\widehat{[mGAP^*]} = \tilde{C_2} - \xi \). Now using Eq. 3.39 to write \(\widehat{[mG]} = \rho ^{mG}_{off} (\tilde{C_2} - \xi ) \widehat{[mG^*]} \), the conservation law given by Eq. 3.37 gives
and since \([mGAP^*] \in \left[ 0,[mGAP_{tot}]\right] \) and the steady states must be nonnegative, we must have
The \(\xi \)-dependent family of steady states is therefore given by
Rights and permissions
About this article
Cite this article
Stolerman, L.M., Ghosh, P. & Rangamani, P. Stability Analysis of a Signaling Circuit with Dual Species of GTPase Switches. Bull Math Biol 83, 34 (2021). https://doi.org/10.1007/s11538-021-00864-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11538-021-00864-w