Evolutionary Suicide of Prey: Matsuda and Abrams’ Model Revisited

Abstract

Under the threat of predation, a species of prey can evolve to its own extinction. Matsuda and Abrams (Theor Popul Biol 45:76–91, 1994a) found the earliest example of evolutionary suicide by demonstrating that the foraging effort of prey can evolve until its population dynamics cross a fold bifurcation, whereupon the prey crashes to extinction. We extend this model in three directions. First, we use critical function analysis to show that extinction cannot happen via increasing foraging effort. Second, we extend the model to non-equilibrium systems and demonstrate evolutionary suicide at a fold bifurcation of limit cycles. Third, we relax a crucial assumption of the original model. To find evolutionary suicide, Matsuda and Abrams assumed a generalist predator, whose population size is fixed independently of the focal prey. We embed the original model into a three-species community of the focal prey, the predator and an alternative prey that can support the predator also alone, and investigate the effect of increasingly strong coupling between the focal prey and the predator’s population dynamics. Our three-species model exhibits (1) evolutionary suicide via a subcritical Hopf bifurcation and (2) indirect evolutionary suicide, where the evolution of the focal prey first makes the community open to the invasion of the alternative prey, which in turn makes evolutionary suicide of the focal prey possible. These new phenomena highlight the importance of studying evolution in a broader community context.

Appendices

Appendix A

In this appendix, we investigate the interior equilibria $(\bar{n}_1,\bar{n}_2,\bar{p})$ of the population dynamics in Eq. (4). Using the notation

$$\begin{aligned} G_1=B(c_1)-d_1, \quad G_2=\frac{\rho _2 c_2}{1+\rho _2 b_2 c_2}-d_2 \end{aligned}$$

for abbreviating the density-independent part of the per capita growth rates as well as

$$\begin{aligned} \phi _1=\frac{q c_1 \beta _1 \bar{n}_1}{1+c_1 \beta _1 h_1 \bar{n}_1}, \quad \phi _2=\frac{(1-q) c_2 \beta _2 \bar{n}_2}{1+c_2 \beta _2 h_2 \bar{n}_2} \end{aligned}$$

(12)

for the Holling II factors, the equilibrium equations (assuming nonzero population densities $\bar{n}_1$, $\bar{n}_2$, $\bar{p}$) are

$$\begin{aligned}&G_1-\delta _1 \bar{n}_1=\phi _1 \bar{p}/\bar{n}_1 \end{aligned}$$

(13a)

$$\begin{aligned}&G_2-\delta _2 \bar{n}_2=\phi _2 \bar{p}/\bar{n}_2 \end{aligned}$$

(13b)

$$\begin{aligned}&\alpha _1 \phi _1+\alpha _2 \phi _2 = \mu \end{aligned}$$

(13c)

First, we express $\bar{n}_1$ and $\bar{n}_2$ from (12),

$$\begin{aligned} \bar{n}_1=\frac{\phi _1}{c_1 \beta _1 (q-h_1 \phi _1)}, \quad \bar{n}_2=\frac{\phi _2}{c_2 \beta _2 (1-q-h_2 \phi _2)} \end{aligned}$$

(14)

Next, we eliminate $\bar{p}$ by dividing (13a) with (13b), and substitute $\bar{n}_1$ and $\bar{n}_2$ with the above expressions to rewrite the equation in terms of $\phi _1$ and $\phi _2$,

$$\begin{aligned} \frac{G_1-\delta _1 \frac{\phi _1}{c_1 \beta _1 (q-h_1 \phi _1)}}{G_2-\delta _2 \frac{\phi _2}{c_2 \beta _2 (1-q-h_2 \phi _2)}} = \frac{c_1 \beta _1 (q-h_1 \phi _1)}{c_2 \beta _2 (1-q-h_2 \phi _2)} \end{aligned}$$

which is rearranged into

$$\begin{aligned}&{[}G_1 c_1 \beta _1 (q-h_1 \phi _1)-\delta _1 \phi _1] c_2^2 \beta _2^2 (1-q-h_2 \phi _2)^2\nonumber \\&\quad =[G_2 c_2 \beta _2 (1-q-h_2 \phi _2) -\delta _2 \phi _2] c_1^2 \beta _1^2 (q-h_1 \phi _1)^2 \end{aligned}$$

(15)

Substituting $\phi _2=(\mu -\alpha _1 \phi _1)/\alpha _2$ from (13c), we obtain a cubic polynomial for $\phi _1$. Each root of this cubic equation yields a root of the equilibrium equations in Eq. (13) with $\phi _2$ from (13c), $\bar{n}_1$ and $\bar{n}_2$ from (14), and $\bar{p}$ from (13a). Figure 29 of Vitale (2016) shows an example where all three roots are real and positive, i.e., biologically admissible equilibria of the model.

If $\alpha _1=0$, then $\phi _2=\mu /\alpha _2$ is a constant independent of $\phi _1$. Therefore, (15) is only quadratic in $\phi _1$, yielding at most two interior equilibria.

Appendix B

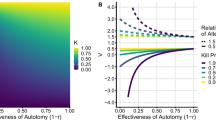
In Sect. 3, we show that evolutionary suicide occurs at a given trait value $c_1^*$ if the birth rate function at this point has a specific value $B(c_1^*)$ given by (8) and a slope $B'(c_1^*)$ in the interval given by inequalities (9) and (10). The figure below shows the width of this interval,

$$\begin{aligned} \sqrt{q \bar{p} \frac{\delta _1}{(c_1^*)^2 h_1}} - \frac{1}{\beta _1} \frac{\delta _1}{(c_1^*)^2 h_1} \end{aligned}$$

Evolutionary suicide is impossible if this width is negative (gray area). The width depends on the chosen value of $c_1^*$ [panel (a)]. It is easy to see also analytically that the width increases with $q \bar{p}$ [all panels] and with $\beta _1$ [panel (b)], and has a maximum as a function of the composite parameter $(c_1^*)^2 (h_1/\delta _1)$ [panels (a), (c) of Fig. 5].

Fig. 5

The width of the interval for $B'(c_1^*)$ that results in evolutionary suicide. The contour lines, starting from the bottom line, correspond to values $0, 0.1, 0.2, \ldots , 0.7$. In the gray area (i.e., below the 0 contour line), condition (7) is violated and hence evolutionary suicide is not possible. Parameter values: a$h_1/\delta _1 = 4, \beta _1 = 1$; b$h_1/\delta _1 = 4, c_1^*=1.2$; c$\beta _1 = 1, c_1^*=1.2$

Appendix C

Here, we consider a well-mixed system where all species are present in one habitat and the predator searches for both prey simultaneously all time. This alternative model is given by

$$\begin{aligned} \frac{\mathrm{d}n_1}{\mathrm{d}t}= & {} \left[ B_1 -d_1-\delta _1 n_1- \frac{c_1 \beta _1 p}{1+c_1 \beta _1 h_1 n_1 + c_2 \beta _2 h_2 n_2} \right] n_1 \end{aligned}$$

(16a)

$$\begin{aligned} \frac{\mathrm{d}n_2}{\mathrm{d}t}= & {} \left[ B_2-d_2-\delta _2 n_2- \frac{c_2 \beta _2 p}{1+c_1 \beta _1 h_1 n_1+c_2 \beta _2 h_2 n_2} \right] n_2 \end{aligned}$$

(16b)

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \left[ \frac{\alpha _1 c_1 \beta _1 n_1+\alpha _2 c_2 \beta _2 n_2}{1+c_1 \beta _1 h_1 n_1 + c_2 \beta _2 h_2 n_2}-\mu \right] p \end{aligned}$$

(16c)

where $B_1$ and $B_2$ abbreviate the birth rates of prey species 1 and 2, respectively. Note that in contrast to Eq. (4), here both prey densities appear in the denominator of the Holling II terms. To interpret this difference, recall that 1 over the denominator of the Holling II functional response gives the fraction of predators that are searching (as opposed to handling an already captured prey). In the model of (16), handling any of the prey in the well-mixed system removes a predator individual from the searching predators. In our main model (4), in a fraction q of its time a predator can only capture, and therefore handle, prey species 1, whereas in the remaining $1-q$ fraction of time it can handle only species 2. Thus, within each time frame, only handling one prey species removes an individual from the searching predators; accordingly, only one prey species appears in the functional response in Eq. (4).

The model in (16) naturally extends to k prey species,

$$\begin{aligned} \frac{\mathrm{d}n_i}{\mathrm{d}t}= & {} \left[ B_i -d_i-\delta _i n_i- \frac{c_i \beta _i p}{1+\sum _{j=1}^k c_j \beta _j h_j n_j} \right] n_i \quad \text {for } i=1,\ldots ,k \quad \end{aligned}$$

(17a)

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \left[ \frac{\sum _{i=1}^k \alpha _i c_i \beta _i n_i}{1+\sum _{j=1}^k c_j \beta _j h_j n_j}-\mu \right] p \end{aligned}$$

(17b)

To find the equilibria, let S denote the number of searching predators,

$$\begin{aligned} S=\frac{p}{1+\sum _{j=1}^k c_j \beta _j h_j n_j} \end{aligned}$$

(18)

At an interior equilibrium of (17), we have

$$\begin{aligned}&B_i -d_i-\delta _i n_i- c_i \beta _i S=0 \quad \text {for } i=1,\ldots ,k \end{aligned}$$

(19a)

$$\begin{aligned}&\frac{1}{\mu }\sum _{i=1}^k \alpha _i c_i \beta _i n_i=1+\sum _{j=1}^k c_j \beta _j h_j n_j \end{aligned}$$

(19b)

This is a linear system for the unknowns $n_1,\ldots ,n_k,S$, and hence generically has only one solution for the equilibrium. The equilibrium value of p follows directly from (18). Since the population dynamics in (16) has a unique interior equilibrium, it cannot undergo a saddle-node bifurcation for any change of the traits such as the foraging effort $c_1$ and the birth rate $B_1$.

The four-species model

$$\begin{aligned} \frac{\mathrm{d}n_1}{\mathrm{d}t}= & {} \left[ B_1 -d_1-\delta _1 n_1- \frac{q c_1 \beta _1 p}{1+c_1 \beta _1 h_1 n_1 + c_3 \beta _3 h_3 n_3} \right] n_1 \end{aligned}$$

(20a)

$$\begin{aligned} \frac{\mathrm{d}n_2}{\mathrm{d}t}= & {} \left[ B_2-d_2-\delta _2 n_2- \frac{(1-q) c_2 \beta _2 p}{1+c_2 \beta _2 h_2 n_2} \right] n_2 \end{aligned}$$

(20b)

$$\begin{aligned} \frac{\mathrm{d}n_3}{\mathrm{d}t}= & {} \left[ B_3-d_3-\delta _3 n_3- \frac{q c_3 \beta _3 p}{1+c_1 \beta _1 h_1 n_1+c_3 \beta _3 h_3 n_3} \right] n_3\end{aligned}$$

(20c)

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \left[ q \frac{\alpha _1 c_1 \beta _1 n_1+\alpha _3 c_3 \beta _3 n_3}{1+c_1 \beta _1 h_1 n_1 + c_3 \beta _3 h_3 n_3} + (1-q) \frac{\alpha _2 c_2 \beta _2 n_2}{1+c_2 \beta _2 h_2 n_2} -\mu \right] p \end{aligned}$$

(20d)

unites the features of our main model in Eq. (4) and the alternative model in (16); here, the focal prey 1 and prey 3 live in the first habitat where the predator spends a fraction q of its time, and the alternative prey 2 lives in the second habitat where the predator spends the remaining fraction $(1-q)$ of its time. This model is briefly mentioned in Discussion.