Skip to main content

Advertisement

SpringerLink
Log in

Threshold Dynamics of a Temperature-Dependent Stage-Structured Mosquito Population Model with Nested Delays

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

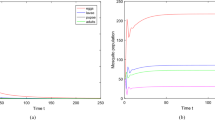
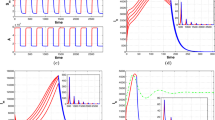
Mosquito-borne diseases remain a significant threat to public health and economics. Since mosquitoes are quite sensitive to temperature, global warming may not only worsen the disease transmission case in current endemic areas but also facilitate mosquito population together with pathogens to establish in new regions. Therefore, understanding mosquito population dynamics under the impact of temperature is considerably important for making disease control policies. In this paper, we develop a stage-structured mosquito population model in the environment of a temperature-controlled experiment. The model turns out to be a system of periodic delay differential equations with periodic delays. We show that the basic reproduction number is a threshold parameter which determines whether the mosquito population goes to extinction or remains persistent. We then estimate the parameter values for Aedes aegypti, the mosquito that transmits dengue virus. We verify the analytic result by numerical simulations with the temperature data of Colombo, Sri Lanka where a dengue outbreak occurred in 2017.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Abdelrazec A, Gumel AB (2017) Mathematical assessment of the role of temperature and rainfall on mosquito population dynamics. J Math Biol 74:1351–1395

    Article  MathSciNet  MATH  Google Scholar 

  • Alto BW, Lounibos LP, Mores CN, Reiskind MH (2008) Larval competition alters susceptibility of adult Aedes mosquitoes to dengue infection. Proc R Soc B 275:463–471

    Article  Google Scholar 

  • Bacaër N, Ait Dads EH (2012) On the biological interpretation of a definition for the parameter \(R_0\) in periodic population models. J Math Biol 65:601–621

    Article  MathSciNet  MATH  Google Scholar 

  • Bacaër N, Guernaoui S (2006) The epidemic threshold of vector-borne diseases with seasonality. J Math Biol 53:421–436

    Article  MathSciNet  MATH  Google Scholar 

  • Beck-Johnson LM, Nelson WA, Paaijmans KP, Read AF, Thomas MB, Bjornstad ON (2013) The effect of temperature on Anopheles mosquito population dynamics and the potential for malaria transmission. PLoS ONE 8(11):e79276

    Article  Google Scholar 

  • Christophers R (1960) Aedes aegypti (L.): the yellow fever mosquito. Cambridge University Press, Cambridge

    Google Scholar 

  • Costa EAPA, Santos EMM, Correia JF, Albuquerque CMR (2010) Impact of small variations in temperature and humidity on the reproductive activity and survival of Aedes aegypti (Diptera: Culicidae). Rev Bras Entomol 54:488–493

    Article  Google Scholar 

  • Diekmann O, Heesterbeek JAP, Metz JAJ (1990) On the definition and the computation of the basic reproduction ratio \(R_0\) in the models for infectious disease in heterogeneous populations. J Math Biol 28:365–382

    Article  MathSciNet  MATH  Google Scholar 

  • Ewing DA, Cobbold CA, Purse BV, Nunn MA, White SM (2016) Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J Theor Biol 400:65–79

    Article  MathSciNet  MATH  Google Scholar 

  • Fang J, Gourley S, Lou Y (2016) Stage-structured models of intra- and inter-specific competition within age classes. J Differ Equ 260:1918–1953

    Article  MathSciNet  MATH  Google Scholar 

  • Hale JK, Verduyn Lunel SM (1993) Introduction to functional differential equations. Springer, New York

    Book  MATH  Google Scholar 

  • Hopp MJ, Foley JA (2001) Global-scale relationships between climate and the dengue fever vector Aedes aegypti. Clim Change 48:441–463

    Article  Google Scholar 

  • Inaba H (2012) On a new perspective of the basic reproduction number in heterogeneous environments. J Math Biol 22:113–128

    MathSciNet  MATH  Google Scholar 

  • Kot M (2001) Elements of mathematical ecology. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Legros M, Lloyd AL, Huang Y, Gould F (2009) Density-dependent intraspecific competition in the larval stage of Aedes aegypti (Diptera: Culicidae): revisiting the current paradigm. J Med Entomol 46(3):409–419

    Article  Google Scholar 

  • Liang X, Zhao X-Q (2007) Asymptotic speeds of spread and traveling waves for monotone semiflows with applications. Commun Pure Appl Math 60:1–40

    Article  MathSciNet  MATH  Google Scholar 

  • Liang X, Zhang L, Zhao X-Q (2017) Basic reproduction ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease). J Dyn Differ Equ. https://doi.org/10.1007/s10884-017-9601-7

    Google Scholar 

  • Liu K, Lou Y, Wu J (2017) Analysis of an age structured model for tick populations subject to seasonal effects. J Differ Equ 263:2078–2112

    Article  MathSciNet  MATH  Google Scholar 

  • Liu-Helmersson J, Stenlund H, Wilder-Smith A, Rocklov J (2014) Vectorial capacity of aedes aegypti: effects of temperature and implications for global dengue epidemic potential. PLoS ONE 9(3):e89783. https://doi.org/10.1371/journal.pone.0089783

    Article  Google Scholar 

  • Lou Y, Zhao X-Q (2017) A theoretical approach to understanding population dynamics with seasonal developmental durations. J Nonlinear Sci 27(2):573–603

    Article  MathSciNet  MATH  Google Scholar 

  • Marinho RA, Beserra EB, Bezerra-Gusmão MA, de Porto VS, Olinda RA, dos Santos CAC (2016) Effects of temperature on the life cycle, expansion, and dispersion of Aedes aegypti (Diptera: Culicidae) in three cities in Paraiba, Brazil. J Vector Ecol 41(1):1–10

    Article  Google Scholar 

  • McCauley E, Nisbet RM, De Roos AM, Murdoch WW, Gurney WSC (1996) Structured population models of herbivorous zooplankton. Ecol Monogr 66:479–501

    Article  Google Scholar 

  • Molnár PK, Kutz SJ, Hoar BM, Dobson AP (2013) Metabolic approaches to understanding climate change impacts on seasonal host-macroparasite dynamics. Ecol Lett 16:9–21

    Article  Google Scholar 

  • Ngarakana-Gwasira ET, Bhunu CP, Mashonjowa E (2014) Assessing the impact of temperature on malaria transmission dynamics. Afr Mat 25:1095–1112

    Article  MathSciNet  MATH  Google Scholar 

  • Nisbet RM, Gurney WS (1982) Modelling fluctuating populations. The Blackburn Press, New Jersey

    MATH  Google Scholar 

  • Nisbet RM, Gurney WS (1983) The systematic formulation of population models for insects with dynamically varying instar duration. Theor Popul Biol 23:114–135

    Article  MathSciNet  MATH  Google Scholar 

  • Omori R, Adams B (2011) Disrupting seasonality to control disease outbreaks: the case of koi herpes virus. J Theor Biol 271:159–165

    Article  MathSciNet  Google Scholar 

  • Rittenhouse MA, Revie CW, Hurford A (2016) A model for sea lice (Lepeophtheirus salmonis) dynamics in a seasonally changing environment. Epidemics 16:8–16

    Article  Google Scholar 

  • Shapiro LLM, Whitehead SA, Thomas MB (2017) Quantifying the effects of temperature on mosquito and parasite traits that determine the transmission potential of human malaria. PLoS Biol 15(10):e2003489. https://doi.org/10.1371/journal.pbio.2003489

    Article  Google Scholar 

  • Simoy MI, Simoy MV, Canziani GA (2015) The effect of temperature on the population dynamics of Aedes aegypti. Ecol Model 314:100–110

    Article  MATH  Google Scholar 

  • Smith HL (1995) Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems. Mathematical surveys and monographs, vol 41. American Mathematical Society, Providence

    Google Scholar 

  • Tatem AJ, Rogers DJ, Hay SI (2006) Global transport networks and infectious disease spread. Adv Parasitol 62:293–343

    Article  Google Scholar 

  • Thieme HR (2009) Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J Appl Math 70:188–211

    Article  MathSciNet  MATH  Google Scholar 

  • Thomé RCA, Yang HM, Esteva L (2010) Optimal control of Aedes aegypti mosquitoes by the sterile insect technique and insecticide. Math Biosci 223:12–23

    Article  MathSciNet  MATH  Google Scholar 

  • van den Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48

    Article  MathSciNet  MATH  Google Scholar 

  • Walter W (1997) On strongly monotone flows. Ann Pol Math 66:269–274

    Article  MathSciNet  MATH  Google Scholar 

  • Wang W, Zhao X-Q (2008) Threshold dynamics for compartmental epidemic models in periodic environments. J Dyn Differ Equ 20:699–717

    Article  MathSciNet  MATH  Google Scholar 

  • Wang X, Zhao X-Q (2017a) A malaria transmission model with temperature-dependent incubation period. Bull Math Biol 79:1155–1182

    Article  MathSciNet  MATH  Google Scholar 

  • Wang X, Zhao X-Q (2017b) Dynamics of a time-delayed Lyme disease model with seasonality. SIAM J Appl Dyn Syst 16(2):853–881

    Article  MathSciNet  MATH  Google Scholar 

  • Wang X, Tang S, Cheke RA (2016) A stage structured mosquito model incorporating effects of precipitation and daily temperature fluctuations. J Theor Biol 411:27–36

    Article  MATH  Google Scholar 

  • Wang Y, Pons W, Fang J, Zhu H (2017) The impact of weather and storm water management ponds on the transmission of West Nile virus. R Soc Open Sci 4:170017. https://doi.org/10.1098/rsos.170017

    Article  Google Scholar 

  • Wilder-Smith A, Gubler DJ (2008) Geographic expansion of dengue: the impact of international travel. Med Clin North Am 92:1377–1390

    Article  Google Scholar 

  • Wu X, Magpantay FMG, Wu J, Zou X (2015) Stage-structured population systems with temporally periodic delay. Math Methods Appl Sci 38:3464–3481

    Article  MathSciNet  MATH  Google Scholar 

  • Yang HM, Macoris MLG, Galvani KC, Andrighetti MTM, Wanderley DMV (2009) Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol Infect 137:1188–1202

    Article  Google Scholar 

  • Zhao X-Q (2017a) Basic reproduction ratios for periodic compartmental models with time delay. J Dyn Differ Equ 29:67–82

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao X-Q (2017b) Dynamical systems in population biology, 2nd edn. Springer, New York, pp 285–315

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, University of Western Ontario, London, ON, N6A 5B7, Canada

    Xiunan Wang & Xingfu Zou

Authors
  1. Xiunan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xingfu Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiunan Wang.

Additional information

This work is supported in part by the NSERC of Canada.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Zou, X. Threshold Dynamics of a Temperature-Dependent Stage-Structured Mosquito Population Model with Nested Delays. Bull Math Biol 80, 1962–1987 (2018). https://doi.org/10.1007/s11538-018-0447-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-018-0447-x

Keywords

Search

Navigation