Abstract
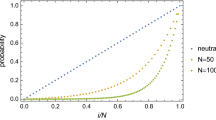
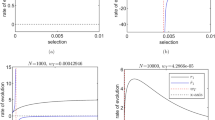
The probability that the frequency of a particular trait will eventually become unity, the so-called fixation probability, is a central issue in the study of population evolution. Its computation, once we are given a stochastic finite population model without mutations and a (possibly frequency dependent) fitness function, is straightforward and it can be done in several ways. Nevertheless, despite the fact that the fixation probability is an important macroscopic property of the population, its precise knowledge does not give any clear information about the interaction patterns among individuals in the population. Here we address the inverse problem: from a given fixation pattern and population size, we want to infer what is the game being played by the population. This is done by first exploiting the framework developed in Chalub and Souza (J Math Biol 75:1735–1774, 2017), which yields a fitness function that realises this fixation pattern in the Wright–Fisher model. This fitness function always exists, but it is not necessarily unique. Subsequently, we show that any such fitness function can be approximated, with arbitrary precision, using d-player game theory, provided d is large enough. The pay-off matrix that emerges naturally from the approximating game will provide useful information about the individual interaction structure that is not itself apparent in the fixation pattern. We present extensive numerical support for our conclusions.






Similar content being viewed by others
References
Alesina A, Galuzzi M (2000) Vincent’s theorem from a modern point of view. Rend Circ Mat Palermo, Ser II Suppl 64:179–191
Allgower E L, Georg K (2012) Numerical continuation methods: an introduction, vol 13. Springer, Berlin
Bürger R (2000) The mathematical theory of selection, recombination and mutation. Wiley, Chichester ISBN 0-471-98653-4/hbk
Chalub FACC, Souza MO (2009) From discrete to continuous evolution models: a unifying approach to drift-diffusion and replicator dynamics. Theor Pop Biol 76(4):268–277
Chalub FACC, Souza MO (2014) The frequency-dependent Wright–Fisher model: diffusive and non-diffusive approximations. J Math Biol 68(5):1089–1133
Chalub FACC, Souza MO (2016) Fixation in large populations: a continuous view of a discrete problem. J Math Biol 72(1–2):283–330
Chalub FACC, Souza MO (2017) On the stochastic evolution of finite populations. J Math Biol 75(6):1735–1774
Chalub FA, Souza MO (2018) Fitness potentials and qualitative properties of the Wright–Fisher dynamics. J Theor Biol 457:57–65 (ISSN 0022-5193)
Czuppon P, Gokhale CS (2018) Disentangling eco-evolutionary effects on trait fixation. Theor Pop Biol 124:93–107
Czuppon P, Traulsen A (2018) Fixation probabilities in populations under demographic fluctuations. J Math Biol 77(4):1233–1277
Ethier SN, Kurtz TG (1986) Markov processes: characterization and convergence. Wiley series in probability and mathematical statistics: probability and mathematical statistics. Wiley, New York (ISBN 0-471-08186-8)
Ewens WJ (2004) Mathematical population genetics. I: theoretical introduction, 2nd edn. Interdisciplinary mathematics 27. Springer, New York
Fisher RA (1922) On the dominance ratio. Proc R Soc Edinb 42:321–341. https://doi.org/10.1007/BF02459576
Gokhale CS, Traulsen A (2010) Evolutionary games in the multiverse. Proc Natl Acad Sci USA 107(12):5500–5504
Gokhale CS, Traulsen A (2014) Evolutionary multiplayer games. Dyn Games Appl 4(4):468–488
Gzyl H, Palacios JL (2003) On the approximation properties of bernstein polynomials via probabilistic tools. Boletín de la Asociación Matemática Venezolana 10(1):5–13
Hartl DL, Clark AG (2007) Principles of population genetics. Sinauer, Massachussets
Hofbauer J, Sigmund K (1998) Evolutionary games and population dynamics. Cambridge University Press, Cambridge
Huang W, Hauert C, Traulsen A (2015) Stochastic game dynamics under demographic fluctuations. Proc Natl Acad Sci 112(29):9064–9069
Imhof LA, Nowak MA (2006) Evolutionary game dynamics in a Wright–Fisher process. J Math Biol 52(5):667–681
Kurokawa S, Ihara Y (2009) Emergence of cooperation in public goods games. Proc R Soc B Biol Sci 276(1660):1379–1384
Lane JM, Riesenfeld RF (1983) A geometric proof for the variation diminishing property of b-spline approximation. J Approx Theory 37(1):1–4
Lessard S (2011) On the robustness of the extension of the one-third law of evolution to the multi-player game. Dyn Games Appl 1(3):408–418
Nowak MA (2006) Evolutionary dynamics: exploring the equations of life. The Belknap Press of Harvard University Press, Cambridge
Pacheco JM, Santos FC, Souza MO, Skyrms B (2009) Evolutionary dynamics of collective action in n-person stag hunt dilemmas. Proc R Soc Lond B Biol Sci 276(1655):315–321
Peña J, Lehmann L, Nöldeke G (2014) Gains from switching and evolutionary stability in multi-player matrix games. J Theor Biol 346:23–33
Phillips GM (2003) Interpolation and approximation by polynomials. CMS books in mathematics. Springer, New York
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C: the art of scientific computing. Cambridge University Press, Cambridge
Rouillier F, Zimmermann P (2004) Efficient isolation of polynomial’s real roots. J Comput Appl Math 162(1):33–50
Smith JM (1982) Evolution and the theory of games. Cambridge University Press, Cambridge
Smith JM, Price GR (1973) The logic of animal conflict. Nature 246(5427):15–18
Souza MO, Pacheco JM, Santos FC (2009) Evolution of cooperation under n-person snowdrift games. J Theor Biol 260(4):581–588
Taylor PD, Jonker LB (1978) Evolutionary stable strategies and game dynamics. Math Biosci 40(1–2):145–156
Taylor HM, Karlin S (1998) An introduction to stochastic modeling, 3rd edn. Academic Press Inc., San Diego, CA ISBN 0-12-684887-4
Wright S (1937) The distribution of gene frequencies in populations. Proc Natl Acad Sci USA 23:307–320
Wright S (1938) The distribution of gene frequencies under irreversible mutations. Proc Natl Acad Sci USA 24:253–259
Wu B, Traulsen A, Gokhale CS (2013) Dynamic properties of evolutionary multi-player games in finite populations. Games 4(2):182–199
Acknowledgements
FACCC was partially supported by FCT/Portugal Strategic Projects UID/MAT/00297/2013 and UID/MAT/00297/2019 (Centro de Matemática e Aplicações, Universidade Nova de Lisboa) and by a “Investigador FCT” grant. MOS was partially supported by CNPq under Grants # 486395/2013-8 and # 309079/2015-2, and by CAPES—Finance Code 001. We also thank the useful comments by two anonymous reviewers, which helped to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chalub, F.A.C.C., Souza, M.O. From Fixation Probabilities to d-player Games: An Inverse Problem in Evolutionary Dynamics. Bull Math Biol 81, 4625–4642 (2019). https://doi.org/10.1007/s11538-018-00566-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-018-00566-w