Skip to main content
SpringerLink
Log in

Outpatient capacity allocation considering adding capacity to match high patient demand

  • Published:
Journal of Systems Science and Systems Engineering Aims and scope Submit manuscript

Abstract

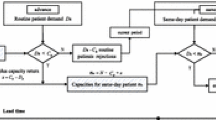
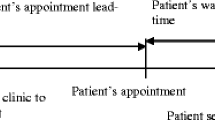
This paper focuses on an outpatient capacity allocation problem where the patient demand is quite higher than the supply. We study an adding capacity policy to mitigate the mismatch between supply and demand. Under this policy, the doctor is allowed to add capacity if all regular capacity have been booked. A capacity allocation model is formulated for both possible no-show routine patients and all show-up same-day patients. The purpose is to determine the number of capacity can be added and how to allocate regular capacity among routine patients and same-day patients, towards maximizing the expected profit, which is composed of the expected income minus the cost of weighted expected doctor’s overload work caused by the adding capacity policy and the cost of rejecting patients. To achieve the aims, we prove the expected profit monotonously decreases when the number of additional capacity exceeds a threshold, and present a two-tier enumeration search algorithm to find the global optimal solution based on the proof. Numerical results indicate that the proposed policy performs well under different levels of demand higher than supply. The optimal number of the additional capacity is hardly affected by varying total expected patient demand. Additionally, under the change of no-show rate, the number of regular capacity allocated to routine patients becomes more stable, compared with the optimal scheme without considering adding capacity policy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bailey, N.T.J. (1952). A study of queues and appointment systems in hospital outpatient departments, with special reference to waiting times. Journal of the Royal Statistical Society, 14: 185–199.

    Google Scholar 

  2. Cayirli, T. & Veral, E. (2003). Outpatient scheduling in health care: a review of literature. Production and Operations Management, 12 (4): 519–549.

    Article  Google Scholar 

  3. Cayirli, T., Veral, E. & Rosen, H. (2006). Designing appointment scheduling systems for ambulatory care services. Health Care Management Science, 9 (1): 47–58.

    Article  Google Scholar 

  4. Cayirli, T., Yang, K.K. & Quek, S.A. (2012). A universal appointment rule in the presence of no-shows and walk-ins. Production and Operations Management, 21 (4): 682–697.

    Article  Google Scholar 

  5. Chakraborty, S., Muthuraman, K. & Lawley, M. (2010). Sequential clinical scheduling with patient no-shows and general service time distributions. IIE Transactions, 42 (5): 354–366.

    Article  Google Scholar 

  6. Chen, R.R. & Robinson, L.W. (2014). Sequencing and scheduling appointments with potential call-in patients. Production and Operations Management, 23 (9): 1522–1538.

    Article  Google Scholar 

  7. Dobson, G., Hasija, S. & Pinker, E.J. (2011). Reserving capacity for urgent patients in primary care. Production and Operations Management, 20 (3): 456–473.

    Article  Google Scholar 

  8. Erdelyi, A. & Topaloglu, H. (2009). Computing protection level policies for dynamic capacity allocation problems by using stochastic approximation methods. IIE Transactions, 41(6):498–510.

    Article  Google Scholar 

  9. Feldman, J., Liu, N., Topaloglu, H. & Ziya, S. (2014). Appointment scheduling under patient preference and no-show behavior. Operations Research, 62 (4): 794–811.

    Article  MathSciNet  MATH  Google Scholar 

  10. Feldman, J. B. & Topaloglu, H. (2015). Capacity constraints across nests in assortment optimization under the nested logit model. Operations Research, 63 (4): 812–822.

    Article  MathSciNet  MATH  Google Scholar 

  11. Gocgun, Y. & Ghate, A. (2012). Lagrangian relaxation and constraint generation for allocation and advanced scheduling. Computers and Operations Research, 39 (10): 2323–2336.

    Article  MathSciNet  MATH  Google Scholar 

  12. Gupta, D. & Denton, B. (2008). Appointment scheduling in health care: challenges and opportunities. IIE Transactions, 40 (9): 800–819.

    Article  Google Scholar 

  13. Hassin, R. & Mendel, S. (2008). Scheduling arrivals to queues: a single server model with no-shows. Management Science, 54 (3): 565–572.

    Article  MATH  Google Scholar 

  14. Izady, N. (2015). Appointment capacity planning in specialty clinics: a queueing approach. Operations Research, 63 (4): 916–930.

    Article  MathSciNet  MATH  Google Scholar 

  15. Kaandorp, G. & Koole, G. (2007). Optimal outpatient appointment scheduling. Health Care Management Science, 10 (3): 217–229.

    Article  Google Scholar 

  16. Kim, S. & Giachetti, R.E. (2006). A stochastic mathematical appointment overbooking model for healthcare providers to improve profits. IEEE Transactions on Systems, Man and Cybernetics Part A-Systems and Humans, 36 (6): 1211–1219.

    Article  Google Scholar 

  17. Klassen, K.J. & Yoogalingam, R. (2009). Improving performance in outpatient appointment services with a simulation optimization approach. Production and Operations Management, 18 (4): 447–458.

    Article  Google Scholar 

  18. Kocabıyıkoğlu, A., Popescu, I. & Stefanescu, C. (2014). Pricing and revenue management: the value of coordination. Management Science, 60 (3): 730–752.

    Article  Google Scholar 

  19. Koeleman, P.M. & Koole, G.M. (2012). Optimal outpatient appointment scheduling with emergency arrivals and general service times. IIE Transactions on Healthcare Systems Engineering, 2 (1): 14–30.

    Article  Google Scholar 

  20. LaGanga, L.R. & Lawrence, S.R. (2007). Clinic overbooking to improve patient access and increase provider productive. Decision Science, 38 (2): 251–276.

    Article  Google Scholar 

  21. Lakshmi, C. & Iyer, S.A. (2013). Application of queueing theory in health care: a literature review. Operations Research for Health Care, 2 (1): 25–39.

    Google Scholar 

  22. Lee, S., Min, D., Ryu, J. & Yih, Y. (2013). A simulation study of appointment scheduling in outpatient clinics open access and overbooking. Simulation: Transactions of the Society for Modeling and Simulation International, 89 (12): 1459–1473.

    Article  Google Scholar 

  23. Liu, N. & Ziya, S. (2014). Panel size and overbooking decisions for appointment-based services under patient no-shows. Production and Operations Management, 23 (12): 2209–2223.

    Article  Google Scholar 

  24. McMullen, M.J. & Netland, P.A. (2015). Lead time for appointment and the no-show rate in an ophthalmology clinic. Clinical Ophthalmology, 9: 513–516.

    Google Scholar 

  25. Murray, M. & Tantau, C. (2000). Same-day appointments: exploding the access paradigm. Family Practice Management, 7 (8): 45–50.

    Google Scholar 

  26. Murray, M. & Berwick, D.M. (2003). Advance access: reducing waiting and delays in primary care. The Journal of the American Medical Association, 289(8): 1035–1039.

    Article  Google Scholar 

  27. Muthuraman, K. & Lawley, M. (2008). A stochastic overbooking model for outpatient clinical scheduling with no-shows. IIE Transactions, 40 (9): 820–837.

    Article  Google Scholar 

  28. Qu, X., Rardin, R.L., Williams, J.A.S. & Willis, D.R. (2007). Matching daily healthcare provider capacity to demand in advanced access scheduling systems. European Journal of Operational Research, 183 (2): 812–826.

    Article  MATH  Google Scholar 

  29. Qu, X., Rardin, R.L., Williams, J.A.S. & Willis, D.R. (2011). Single versus hybrid time horizons for open access scheduling. Computers and Industrial Engineering, 60 (1): 56–65.

    Article  Google Scholar 

  30. Qu, X., Rardin, R.L. & Williams, J.A.S. (2012). A mean variance model to optimize the fixed versus open appointment percentages in open access scheduling systems. Decision Support Systems, 53 (3): 554–564.

    Article  Google Scholar 

  31. Ratcliffe, A., Gilland, W. & Marucheck, A. (2012). Revenue management for outpatient appointments: joint capacity control and overbooking with class-dependent no-shows. Flexible Services and Manufacturing Journal, 24 (4): 516–548.

    Article  Google Scholar 

  32. Robinson, L.W. & Chen, R.R. (2010). A comparison of traditional and open-access policies for appointment scheduling. Manufacturing and Service Operations Management, 12 (2): 330–346.

    Article  Google Scholar 

  33. Schuetz, H.J. & Kolisch, R. (2012). Approximate dynamic programming for capacity allocation in the service industry. European Journal of Operational Research, 218 (1): 239–250.

    Article  MathSciNet  MATH  Google Scholar 

  34. Schuetz, H.J. & Kolisch, R. (2013). Capacity allocation for demand of different customer-product-combinations with cancellations, no-shows, and overbooking when there is a sequential delivery of service. Annals of Operations Research, 206 (1): 401–423.

    Article  MathSciNet  MATH  Google Scholar 

  35. Steinbauer, J.R., Korell, K., Erdin, J. & Spann, S.J. (2006). Implementing open-access scheduling in an academic practice. Family Practice Management, 13 (3): 59–64.

    Google Scholar 

  36. Tang, J., Yan, C. & Cao, P. (2014). Appointment scheduling algorithm considering routine and urgent patients. Expert Systems with Applications, 41 (10): 4529–4541.

    Article  Google Scholar 

  37. Truong, V.A. (2015). Optimal advance scheduling. Management Science, 61 (7): 1584–1597.

    Article  Google Scholar 

  38. Turkcan, A., Zeng, B., Muthuraman, K. & Lawley, M. (2011). Sequential clinical scheduling with service criteria. European Journal of Operational Research, 214 (3): 780–795.

    Article  MATH  Google Scholar 

  39. Wright, C.P., Groenevelt, H. & Shumsky, R.A. (2010). Dynamic revenue management in airline alliances. Transportation Science. 44 (1): 15–37.

    Article  Google Scholar 

  40. Zeng, B., Turkcan, A., Lin, J. & Lawley, M. (2010). Clinic scheduling models with overbooking for patients with heterogeneous no-show probabilities. Annals of Operations Research. 178 (1): 121–144.

    Article  MathSciNet  MATH  Google Scholar 

  41. National Health and Family Planning Commission of the People’s Republic of China. (2014). Statistical bulletin on the development of health and family planning in China in 2013. http://www.moh.gov.cn/guihuaxxs/s10742/220140/886f82dafa344c3097f1d16581a1bea2.shtml. Cited May 30, 2014.

    Google Scholar 

Download references

Acknowledgments

This research is supported in part by the National Natural Science Foundation of China under Grant 71420107028, in part by Hong Kong Research Grant Council under Grant T32-102/14-N and in part by the National Natural Science Foundation of China under Grant 71501027.

Author information

Authors and Affiliations

  1. Institute of Systems Engineering, Northeastern University, Shenyang, 110819, China

    Bowen Jiang

  2. College of Management Science and Engineering, Dongbei University of Finance and Economics, Dalian, 116025, China

    Jiafu Tang & Chongjun Yan

Authors
  1. Bowen Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiafu Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chongjun Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiafu Tang.

Additional information

Bowen Jiang is a PhD student in the Institute of Systems Engineering at Northeastern University, Shenyang. His research interests are in the areas of outpatient appointment management.

Jiafu Tang is a ChangJiang Scholarship Chair Professor. He is the Head of College of Management Science and Engineering at Dongbei University of Finance and Economics, Dalian. His research interests are in the areas of production and operations optimization in manufacturing systems and service systems, and operation planning in health care service.

Chongjun Yan is a lecturer in the College of Management Science and Engineering at Dongbei University of Finance and Economics, Dalian. His research interests are in the areas of operation planning in health care service.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, B., Tang, J. & Yan, C. Outpatient capacity allocation considering adding capacity to match high patient demand. J. Syst. Sci. Syst. Eng. 26, 487–516 (2017). https://doi.org/10.1007/s11518-017-5350-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11518-017-5350-8

Keywords

Search

Navigation