Skip to main content
SpringerLink
Log in

Supply chain performance for deteriorating items with cooperative advertising

  • Published:
Journal of Systems Science and Systems Engineering Aims and scope Submit manuscript

Abstract

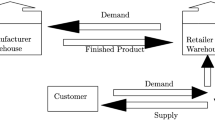
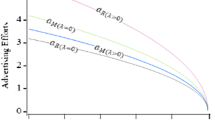
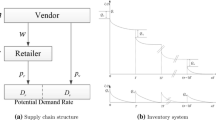
To study the effect of cooperative advertising on the supply chain of deteriorating items, this paper establishes a Stackelberg game model for a two-echelon deteriorating items supply chain composed of one manufacturer and one retailer under a given support program with an exogenous participation rate. The manufacturer as the leader determines the wholesale price and production rate, and the retailer as the follower determines the retail price and advertising strategies. The strategies of the players under the decentralized scenario and the centralized scenario are respectively characterized. Numerical simulations and sensitivity analysis are conducted to gain some managerial insights. It is shown that the pricing, advertising and production strategies are negatively correlated to deteriorating coefficient, and both the profit and the channel efficiency decrease with deteriorating coefficient; The interaction between price, advertising investment and production rate results in a higher retail price of the centralized channel compared to that of the decentralized channel; Implementing the cooperative advertising program does improve the performance of the supply chain in some cases and the participation rate roughly at 0.5 is most preferable, but it is also possible to distort incentive and damage the channel performance when the participation rate reaches a relatively high level.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aust, G. & Buscher, U. (2012). Vertical cooperative advertising and pricing decisions in a manufacturer-retailer supply chain: a game-theoretic approach. European Journal of Operational Research, 223 (2): 473–482.

    Article  MathSciNet  MATH  Google Scholar 

  2. Aust, G. & Buscher, U. (2014). Cooperative advertising models in supply chain management: a review. European Journal of Operational Research, 234 (1): 1–14.

    Article  MathSciNet  MATH  Google Scholar 

  3. Bakker, M., Riezebos, J. & Teunter, R. H. (2012). Review of inventory systems with deterioration since 2001. European Journal of Operational Research, 221 (2): 275–284.

    Article  MathSciNet  MATH  Google Scholar 

  4. Chern, M. S., Pan, Q. H., Teng J. T., Chan Y. L. & Chen, S. C. (2013). Stackelberg solution in a vendor-buyer supply chain model with permissible delay in payments. International Journal of Production Economics, 114 (1): 397–404.

    Article  Google Scholar 

  5. Deane, J. & Agarwal, A. (2012). Scheduling online advertisements tomaximize revenue under variable display frequency. Omega-International Journal of Management Science, 40 (5): 562–570.

    Article  Google Scholar 

  6. De Giovanni, P. (2011). Quality improvement vs. advertising support: which strategy works better for a manufacturer? European Journal of Operational Research, 208 (1): 119–130.

    MATH  Google Scholar 

  7. Dockner, E. J., Jørgensen, S., Long, N. V. & Sorger, G. (2000). Differential Games in Economics and Management Science. Cambridge, UK: Cambridge University Press.

    Book  MATH  Google Scholar 

  8. Erickson, G. M. (2009). Advertising competition in a dynamic oligopoly with multiple brands. Operations Research, 57 (5): 1106–1113.

    Article  MATH  Google Scholar 

  9. Erickson, G. M. (2011). A differential game model of the marketing operations interface. European Journal of Operational Research, 211 (2): 394–402.

    Article  MathSciNet  MATH  Google Scholar 

  10. Erickson, G. M. (2012). Transfer pricing in a dynamic marketing-operations interface. European Journal of Operational Research, 216 (2): 326–333.

    Article  MathSciNet  MATH  Google Scholar 

  11. Feichtinger, G. & Hartl, R. (1985). Optimal pricing and production in an inventory model. European Journal of Operational Research, 19 (1): 45–56.

    Article  MathSciNet  MATH  Google Scholar 

  12. Feichtinger, G., Hartl, R. & Sethi, S. (1985). Dynamic optimal control models in advertising: recent developments. Management Science, 40 (2): 195–226.

    Article  MATH  Google Scholar 

  13. Ferguson, M. & Ketzenberg, M. E. (2006). Information sharing to improve retail product freshness of perishables. Production and Operations Management, 15 (1): 57–73.

    Google Scholar 

  14. Ghare, P. M. & Schrader, G. F. (1963). A model for an exponentially decaying inventory. Journal of Industrial Engineering, 14(5):238–243.

    Google Scholar 

  15. Goyal, S. K. & Giri, B. C. (2001). Recent trends in modeling of deteriorating inventory. European Journal of Operational Research, 134 (1): 1–16.

    Article  MathSciNet  MATH  Google Scholar 

  16. He, X., Prasad, A. & Sethi, S. (2007). A survey of Stackelberg differential game models in supply marketing channels. Journal of Systems Science and Systems Engineering, 16 (4): 385–413.

    Article  Google Scholar 

  17. He, X., Pasad, A. & Sethi, S. (2009). Cooperative advertising and pricing in a dynamic stochastic supply chain: feedback Stackelberg strategies. Production and Operations Management, 18 (1): 78–94.

    Google Scholar 

  18. Hill, R. M. (1995). Inventory model for increasing demand followed by level demand. Journal of the Operational Research Society, 46 (10): 1250–1259.

    Article  MATH  Google Scholar 

  19. Jørgensen, S., Kort, P. M. & Zaccour, G. (1999). Production, inventory, and pricing under cost and demand learning effects. European Journal of Operational Research, 117 (2): 382–395.

    Article  MATH  Google Scholar 

  20. Jørgensen, S. & Zaccour, G. (1999). Equilibrium pricing and advertising strategies in a marketing channel. Journal of Optimization Theory and Applications, 102 (1): 111–125.

    Article  MathSciNet  MATH  Google Scholar 

  21. Jørgensen, S., Sigué, S. P. & Zaccour, G. (2000). Dynamiccooperative advertising in a channel. Journal of Retailing, 76 (1): 71–92.

    Article  Google Scholar 

  22. Jørgensen, S., Taboubi, S. & Zaccour, G. (2003). Retail promotions with negative brand image effects: is cooperation possible? European Journal of Operational Research, 150 (2): 395–405.

    Article  MathSciNet  MATH  Google Scholar 

  23. Karray, S. & Martín-Herrán, G. (2009). A dynamic model for advertising and pricing competition between national and store brands. European Journal of Operational Research, 193 (2): 451–467.

    Article  MathSciNet  MATH  Google Scholar 

  24. Karray, S. & Zaccour, G. (2006). Could co-op advertising be a manufacturer's counter strategy to store brands? Journal of Business Research, 59 (9): 1008–1015.

    Article  Google Scholar 

  25. Li, R., Lan, H. & Mawhinney, J. R. (2010). A review on deteriorating inventory study. Journal of Service Science and Management, 3 (1): 117–129.

    Article  Google Scholar 

  26. Liu, W. W., Tang, W. S., Feng, L. & Zhang, J. X. (2014). Dynamic pricing under temperature control for perishable foods. Journal of Systems Science and Systems Engineering, 23 (3): 252–265.

    Article  Google Scholar 

  27. Mosca, S. & Viscolani, B. (2004). Optimal goodwill path to introduce a new product. Journal of Optimization Theory and Applications, 123: 149–162.

    Article  MathSciNet  MATH  Google Scholar 

  28. Nagler, M. G. (2006). An exploratory analysis of the determinants of cooperative advertising participation rates. Marketing Letters, 17 (2): 91–102.

    Article  Google Scholar 

  29. Nerlove, M. & Arrow, L. (1962). Optimal advertising policy under dynamic considerations. Economica, 29 (114): 129–142.

    Article  Google Scholar 

  30. Panda, S., Senapati, S. & Basu, M. (2008). Optimal replenishment policy for perishable seasonal products in a season with ramp-type time dependent demand. Computers & Industrial Engineering, 54 (2): 301–314.

    Article  Google Scholar 

  31. Sayadi, M. K. & Makui, A. (2014). Feedback Nash equilibrium for dynamic brand and channel advertising in dual channel supply chain. Journal of Optimal Theory and Applications, 161 (3): 1012–1021.

    Article  MathSciNet  MATH  Google Scholar 

  32. Skouri, K. & Papachristos, S. (2003). Optimal stopping and restarting production times for an EOQ model with deteriorating items and time-dependent partial backlogging. International Journal of Production Economics, 81-82: 525–531.

    Article  Google Scholar 

  33. Skouri, K., Konstantaras, I., Papachristos, S. & Ganas, I. (2009). Inventory models with ramp type demand rate, partial backlogging and Weibull deterioration rate. European Journal of Operational Research, 192 (1): 79–92.

    Article  MathSciNet  MATH  Google Scholar 

  34. Teng, J. T. & Chang, C. T. (2005). Economic production quantity models for deteriorating items with price-and stock-dependent demand. Computers & Operations Research, 32 (2): 279–308.

    Article  MathSciNet  MATH  Google Scholar 

  35. Wang, X. & Li, D. (2012). A dynamic product quality evaluation based pricing model for perishable food supply chains. Omega-International Journal of Management Science, 40 (6): 906–917.

    Article  MathSciNet  Google Scholar 

  36. Wee, H. M. (1993). Economic production lot size model for deteriorating items with partial back ordering. Computers & Industrial Engineering, 24 (3): 449–458.

    Article  Google Scholar 

  37. Whitin, T. M. (1957). Theory of Inventory Management. Princeton University Press, Princeton, NJ.

    Google Scholar 

  38. Xiao, T. J. & Xu, T. T. (2013). Coordinating price and service level decisions for a supply chain with deteriorating item under vendor managed inventory. International Journal of Production Economics, 145 (2): 734–752.

    Article  Google Scholar 

  39. Yang, P. C. & Wee H. M. (2003). An integrated multi-lot-size production inventory model for deteriorating item. Computers & Operations Research, 30 (5): 671–682.

    Article  MATH  Google Scholar 

  40. Zhang, J., Gou, Q. L., Liang, L. & Huang, Z. M. (2013). Supply chain coordination through cooperative advertising with reference price effect. Omega-International Journal of Management Science, 41 (2): 345–353.

    Article  Google Scholar 

  41. Zhou, M. Y. & Lin, J. (2014). Cooperative advertising and pricing models in a dynamic marketing channel. Journal of Systems Science and Systems Engineering, 23 (1): 94–110.

    Article  Google Scholar 

Download references

Acknowledgments

The authors thank the editors and two anonymous referees for their helpful comments and suggestions that substantially improved this paper. This work was supported by the National Nature Science Foundation of China No. 61473204, Humanity and Social Science Youth Foundation of Ministry of Education of China No. 14YJCZH204, and the Program for New Century Excellent Talents in Universities of China No. NCET-11-0377.

Author information

Authors and Affiliations

  1. College of Management and Economics, Tianjin University, Tianjin, 300072, China

    Jianxiong Zhang, Jianqi Li, Lihao Lu & Rui Dai

Authors
  1. Jianxiong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianqi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lihao Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Rui Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lihao Lu.

Additional information

Jianxiong Zhang was born in Hunan province, China, in 1979. He received the BS degree in mechanical engineering and MS, PHD degrees in systems engineering from the Tianjin University, Tianjin, China, in 2002, 2004 and 2006, respectively. He is currently a professor at the College of Management and Economics, Tianjin University, Tianjin, China. His current research interests include dynamical supply chain management, modeling and control for complex systems. He has published more than 50 journal papers such as in Annals of Operations Research, International Journal of Production Research, Omega, Journal of the Operational Research Society, Journal of Optimization Theory and Applications, IEEE Transactions on Neural Networks, Neural Computation, Pattern Recognition, International Journal of Robust and Nonlinear Control, Nonlinear Dynamics, etc.

Jianqi Li was born in Anhui province, China, in 1992. He is a graduate student in the College of Management and Economics, Tianjin University. He earned his BS in School of Science from Dalian Ocean University. His current research interests include control theory, dynamic pricing and differential games.

Lihao Lu was born in Hebei province, China, in 1986. He is a PHD candidate in the College of Management and Economics, Tianjin University. He earned his BS in School of Science from Dalian Ocean University, and MS in systems engineering from Tianjin University. He has published paper in International Journal of Systems Science. His current research interests include control theory, dynamic pricing and differential games.

Rui Dai was born in Jiangxi province, China, in 1988. She is a PHD candidate in the College of Management and Economics, Tianjin University. She earned her BS in electrical and electronic engineering from East China Jiaotong University, and MS in electrical and computer engineering from University of Massachusetts at Amherst. Her current research interests include control theory, green supply chain management, dynamic pricing and differential games.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Li, J., Lu, L. et al. Supply chain performance for deteriorating items with cooperative advertising. J. Syst. Sci. Syst. Eng. 26, 23–49 (2017). https://doi.org/10.1007/s11518-015-5279-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11518-015-5279-8

Keywords

Search

Navigation