Abstract
Electric contact currents (CC) can cause muscle contractions, burns, or ventricular fibrillation which may result in life-threatening situations. In vivo studies with CC are rare due to potentially hazardous effects for participants. Cadaver studies are limited to the range of tissue’s electrical properties and the utilized probes’ size, relative position, and sensitivity. Thus, the general safety standards for protection against CC depend on a limited scientific basis. The aim of this study was therefore to develop an extendable and adaptable validated numerical body model for computational CC dosimetry for frequencies between DC and 1 MHz. Applying the developed model for calculations of the IEC heart current factors (HCF) revealed that in the case of transversal CCs, HCFs are frequency dependent, while for longitudinal CCs, the HCFs seem to be unaffected by frequency. HCFs for current paths from chest or back to hand appear to be underestimated by the International Electrotechnical Commission (IEC 60479-1). Unlike the HCFs provided in IEC 60479-1 for longitudinal current paths, our work predicts the HCFs equal 1.0, possibly due to a previously unappreciated current flow through the blood vessels. However, our results must be investigated by further research in order to make a definitive statement. Contact currents of frequencies from DC up to 100 kHz were conducted through the numerical body model Duke by seven contact electrodes on longitudinal and transversal paths. The resulting induced electric field and current enable the evaluation of the body impedance and the heart current factors for each frequency and current path.
Similar content being viewed by others
1 Introduction
Electric contact currents (CCs) occur when one or more body parts (e.g., the hand) touch a conducting object with an electric potential that is different from that of the body. Protection against CCs at frequencies below 1 MHz is needed to prevent painful muscle contractions, burns, or ventricular fibrillation (VF), which is the main cause of deaths by CCs [1]. Additionally, secondary injuries and psychological problems can be triggered [2,3,4,5,6,7]. Since the myocardial cells become more and more insensitive with increasing frequencies, the tissue is more likely to be burned before it is excited at higher frequencies [8].
The risk assessment of CC dates from the mid-1900s. Osypka [9] and Dalziel and Lee [10,11,12] contributed by determining the total body current thresholds marking the perception, let-go, and VF thresholds. The threshold of perception marks the minimal value of the current through the body that can be perceived by a person. The threshold of let-go describes the maximal value of the current through the body at which an individual is able to release the energized contact area. There is no let-go threshold for direct currents, only at the start and the end of the current flow leads to painful and seizure-like muscle contractions. In the early 1970s, the International Electrical Commission (IEC) combined these physiological thresholds with body impedance measurements from Freiberger [13] to derive a set of international standards [1, 14,15,16]. Since then, these standards have been updated several times based on results from studies such as those of Biegelmeier et al. [17, 18]. Since introducing the so-called heart current factor (HCF) [19], these standards consider the dependence of the VF risk on current paths, taking into account that, e.g., a current path from hand to feet drives a larger portion of the total body current through the heart (higher HCF) than a current path from foot to foot (lower HCF). In other words, VF is more likely to occur in a person when the current enters the body through the hand and exits through the feet than when the current enters the body through one foot and exits through the other foot. IEC 60479-1 gives HCFs to scale risks of VF for 16 different current paths [1]. Furthermore, the International Commission on Non-Ionizing Radiation Protection [20] and the Institute of Electrical and Electronics Engineers (IEEE) address the effect of CCs in their recommendations [20,21,22].
The scientific basis for standards on CCs is very limited, especially regarding frequencies other than DC and 50/60 Hz as well as in the number of study participants [1]. In vivo experiments with CC are rare due to potentially hazardous or painful effects for participants. Important internal field distribution measurements of vulnerable body areas were only carried out using body phantoms [9] and in cadaver studies [13, 23], where probes were inserted into the body around the heart in order to estimate HCFs. The outcome is therefore limited to cadaver tissue’s electrical properties as well as to the size, position, and sensitivity of the utilized probes.
Due to these limitations in experimental studies, numerical approaches were proposed and carried out. Early studies of Brucher et al. [24,25,26] and Biegelmeier et al. [27] lacked investigations of frequencies other than 50/60 Hz, high-resolution body models, and tissue segmentations. Studies using high-resolution anatomical body models, scrutinize intermediate and radio frequency currents on current paths from fingertip to feet [28, 29], validate their numerical methods with analytical models [29, 30], and assess skeletal muscle anisotropies and skin properties at 50 Hz [30]. These studies, however, show neither body model validation attempts with in vivo data nor evaluations of different current paths as suggested by the IEC [1]. Only two studies [31, 32] considered different current paths (HCFs), but both were limited to 50 Hz. Additionally, they lack validation of the used body models and numerical method. In general, there exists no peer-reviewed literature on HCFs besides 50 Hz studies, even though VF can occur in a wide frequency range (DC to 100 kHz) [8].
To address this limitation, our study presents computational methods for dosimetric studies on CCs using a resistive-capacitive high-resolution anatomical body model in the frequency range from DC to 1 MHz focusing on internal field distributions and the potential risk of VF. Based on a recent research agenda published by Reilly, Hirata [33], in this study, special attention was directed to model validation, tissue anisotropy, and skin properties. The aim was to develop an extendable and adaptable validated toolbox for computational dosimetry studies on CCs enabling assessments based on the generated data sets using electrical cell-stimulation modeling and future investigation with new body models.
2 Methods
2.1 Simulation setup
The computational simulation platform Sim4Life version 2.2.3 and the high-resolution anatomic body model “Duke” [34] version 3.1 were used for all simulations applying Sim4Life’s “Electro Quasi-Static” solver based on the finite element method. The Electro Quasi-Static solver is applicable for the calculation of electric fields in the (extremely) low-frequency range (f < 1 MHz) and considers both the conductivity and the relative permittivity of the body tissues.
Sim4Life was running on a workstation with 2 Intel Xenon CPUs E5-2650v3 (2.3 GHz) and 128 GB RAM. The voxel edge length of Duke was set to 1 mm in the heart, and 2–3 mm for the remaining tissue. The maximum edge length relation relaxation gives the percentage of local relaxation of the grading ratio to increase the dynamics of the gridder without risking over-refinement in areas with closely spaced grid lines. It was set to 20% to ensure a highly homogenous resolution in the thorax region.
Overall, seven contact electrodes (100 × 100 mm) were positioned according to the IEC [1, 23] positions at the right/left hand (RH/LH), right/left foot (RF/LF), posterior thorax (PT), anterior thorax (AT), and (posterior) seat [35]. All 16 IEC current paths can be simulated with the seven contact electrodes. The current paths are abbreviated in the following manner:
-
A current path from the RH to the LH is abbreviated as RH-LH.
-
A current path from both hands (BH) to both feet (BF) is abbreviated as BH-BF.
-
A current path from LH to any combination of foot or feet is abbreviated as LH-xF.
The CC scenario was implemented as a voltage-driven problem, meaning the voltage level (touch voltage) of the touched conductive object (here the contact electrodes) was set to a fixed value/amplitude and the resulting total body current (IBody) was measured with four surface integrals over the numerically derived internal electric field. Through Ohm’s law, the total body impedance (ZTotal) is quantifiable for every current path, touch voltage, and current frequency.
The validity of body model’s electrical properties is described in the following subsections. If not stated otherwise, the body models’ segmented tissues were linked to the tissue electrical properties database version 2.7 of the Foundation for Research on Information Technologies in Society (IT’IS) [36], which mainly refers to Gabriel et al. [37,38,39,40]. This database provides conductivity and relative permittivity values for all used tissues as a function of frequency.
2.2 Skeletal muscle anisotropy
The electrical properties of human skeletal muscles are anisotropic at low frequencies (f < 1 MHz), meaning they differ considerably with the direction of the current [35, 38]. The conductivity of skeletal muscle is therefore often measured along (longitudinal) and across (transversal) the muscle fibers. This definition of longitudinal and transversal must not be confused with the longitudinal or transversal current paths through the body. Since the skeletal muscles and therefore also the muscle fibers are oriented proximally or distally (e.g., wrist root to elbow for the forearm or ankle to knee for the lower leg), the main part of the CCs is expected to traverse the skeletal muscles longitudinally. Prior numeric assessments [30, 41, 42] of skeletal muscle assumed anisotropy ratios (longitudinal/transversal) of between 1.7 and 2 for 50 Hz currents, which lies within the range of literature values reviewed by Gabriel et al. [38]. Thus, they show no major differences between an anisotropic setup and an isotropic setup using the longitudinal conductivity value [30]. Thus, the skeletal muscle fiber tissue was set to the longitudinal conductivity values according to Gabriel et al. [37].
2.3 Body models’ internal and total impedance
The total body impedance ZTotal of humans can be split into the skin impedance (ZSkin) of the surface area which is in contact with the voltage source (i.e., contact area) in series with the internal body impedance ZIntern. The internal body impedance is mostly dependent on the current path, and is mainly resistive and its change with frequency is negligible [1]. ZSkin is often described as a resistive-capacitive network and its impedance decreases with rising frequencies (f). This model has been used and proven correctly in numerous studies and was therefore also implemented in the safety standards IEC 60479-1[1] and IEC 60990 [43] with defined values for the different elements of the RC circuit. ZSkin drops significantly above 10 kHz. In cases of CCs with extremely low frequencies (ELF; f < 1 kHz) the skin impedance is strongly dependent on the touch voltage Ut. At higher voltages (Ut > 220 V) the skin impedance decreases drastically and becomes negligible when the current forces skin breakdown [1, 17]. Thus, at frequencies higher than 10 kHz and touch voltages higher than 220 V, ZTotal approximates ZIntern. At frequencies between 1 and 10 kHz, the question of whether or not the skin impedance is negligible needs to be assessed on a case by case basis.
In view of ZTotal as the limiting factor for the total body current (IBody), the dependency of ZSkin on the touch voltage and the frequency becomes a key factor in the modeling of CCs [44]. In order to cover exposure scenarios where ZSkin needs to be considered and where it can be neglected, two body models were developed. The Internal Body Model (Intern-BM) considers only ZIntern and the Total Body Model (Total-BM) considerers both ZIntern and ZSkin. An overview of the body model classification for different accident scenarios is given in Table 1.
2.4 Total-BM and intern-BM implementation
For the Total-BM, the electrical properties of the skin were adapted to match the impedance values derived from IEC 60479-1 [1]. In order to achieve that, the skin at the contact areas was removed and the touch voltage and frequency-dependent electric properties of the skin were implemented as a 2-mm thick slice of the contact electrode resembling ZSkin (cf. Table 2). In that way, it is possible to control the electrical properties of ZSkin at every position of the electrode and to ensure an exact contact of 10 × 10 cm2. Following IEC 60479-1, this is defined as a “large surface area.” The remaining material of the contact electrode was assigned to a value of 1.0 Sm−1 in order to be magnitudes higher than the skin conductivity value at ELF of 0.2 mSm−1 [36]. At 1.0 Sm−1, the influence of the remaining material can be considered insignificant for the assessed parameters (ZIntern, ZTotal, and the HCF). A higher conductivity value causes solver instability because it spreads the range of material parameters beyond the greatest possible dynamic range of the solver. The results for voltage and frequency-dependent skin conductivity are listed in Table 2.
For the Intern-BM, the 2-mm layer resembling ZSkin was removed so that the touch voltage is in direct contact with tissue underlying the skin, enabling simulations of exposure scenarios where the skin impedance influence is considered negligible (cf. Table 1). The contact area varies with the contact electrode positions between 70 and 100 cm2 due to the three-dimensional body surface. However, ZIntern is not dependent on the contact area and therefore the contact area can vary for the Intern-BM [1].
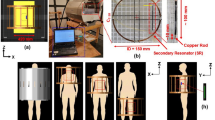
Figure 1 gives an overview of all model features. Of note, for studies focusing on tissues directly underlying the skin, this method is most likely unsuitable.
a Duke anatomic body model with the seven contact electrodes and the four surface integrals for the total body current (IBody) measurement. b Voxels view of the LH with its contact electrode and the simulation setup. 1. Boundary condition (Ut on green grid), 2. Red slice resembles ZSkin, which is removed when using Intern-BM 3. Contact electrode material with 1 Sm−1. c Voxels of the LH and the contact area where the skin is removed and the underlying tissue (e.g., subcutaneous adipose tissue; yellow) is visible
2.5 Model validation
In order to validate the presented approach, the net electrical properties of the body models (the total body impedance ZTotal) were calculated and compared to in vivo body impedance measurement values from literature either considering different touch voltages [1, 13, 17] or higher frequencies [47, 48]. All these studies used similar exposure conditions (e.g., current path: RH-LH and RH-BF, contact area) enabling the comparison with the Intern- and the Total-BM.
2.6 HCF simulations
For every current path, a different portion of the total current is being driven through the heart. To consider this effect HCFs were introduced [1]. HCFs are therefore important for determining the risk of VF due to CCs in different paths. The measurements of Sam [19] are of special importance in this context since they are the literature basis for the IEC [1] HCF values. Sam [19] applied CCs due to 220 V touch voltages to human cadavers. He compared the influence of DC and 50 Hz AC for different voltages on the body resistance and concluded that for voltages above 100 V, the difference is negligible. Therefore, he inserted six electrodes at the base, apex, front, back, top, and bottom of the cadavers’ hearts and measured three orthogonal voltages across the heart (base to apex, front to back, and top to bottom) at 50 Hz. By dividing the measured voltages by the distance of the electrodes (85–160 mm), Sam approximated the electric field (EF) vector (ESam) for the heart region by assuming a unidirectional homogenous EF distribution and a negligible error due to differing electrode distances. A heterogeneous EF distribution is not assessable with Sam’s method because of the averaging effect due to the probe size and locally changing EF vector orientations.
Sam calculated his HCF (FSam) for a given current path p by dividing ESam by the total body current (IBod) to eliminate the effects of changing body impedances due to the different current paths. For simplicity, this term is here normalized on the current path LH-BF (pLH–BF) at a given frequency, because Sam did not consider a frequency dependency in his equation, as explained in the previous paragraph.
Sam’s [19] HCF measurements were modeled numerically in order to compare the results of our numerical model (cf. Fig. 2) with the cadaver measurements. Three orthogonal line integrals modeling the voltage measurements were implemented into the computational model with a local resolution of 1 mm (cf. black lines in Fig. 2(a)). For clarification, Fig. 2(b) shows the electric field vectors along two of the three line integrals. The HCF of the numerically modeled Sam method will be referred to with FSamNum.
a Computational imitation of Sam [19]. Thorax bones, heart muscle, and three orthogonal line integrals as imitation of Sam’s voltage measurements. b The electric field vectors along the line integral from base to apex and top to bottom. c Cross-section slice parallel to the frontal plane
The voxels of the ventricular myocardium (VM) and the left ventricle lumen (LV) are shown. The EF of the ventricle for every voxel in the slice is displayed. It is shown how only the ventricle myocardium voxels of this slice are selected (highlighted) as an example of how the data for E99Heart is selected for all the slices of the heart.
For our study, a novel HCF assessment method was developed taking advantage of numerical simulations being able to provide the local EF distribution in the heart muscle. Therefore, the 99th percentile (cf. guidelines from the International Commission on Non-Ionizing Radiation Protection (ICNIRP [20])) of the EF distribution in the ventricle myocardium (E99Heart) was calculated for all 16 current paths (cf. Section 2.1) and five different frequencies (DC, 50 Hz, 1 kHz, 10 kHz, 100 kHz). Accordingly, E99Heart (p, f) is noted as a function of current path and frequency. To enable a comparison to Sam’s [19], the numerical HCF (F99Num) is also normalized on the current path LH-BF (pLH–BF) (cf. (1) and (2)).
In order to clarify which part of the heart muscle was considered, the corresponding electric field of a slice of the ventricle myocardium is shown in Fig. 2(c). The slice is orientated parallel to the frontal plane. For E99Heart, the whole ventricle myocardium was considered, since this is the part of the heart muscle where fibrillation is induced.
All HCF methods were applied on all 16 current paths defined in Section 2.1. The Intern-BM was used for all HCF calculations, because the skin impedance has no influence on the HCF.
3 Results and discussion
3.1 Model validation
Figure 3 demonstrates the validation of the net impedance of the body models developed in this study. The Intern-BM (red triangles) is consistent with the literature values where the skin’s impedance contribution to ZTotal is negligible, either due to high touch voltages (cf. IEC 1000 V curve) or frequencies above 1 kHz (cf. De Santis or Chatterjee curves). The exceeding of De Santis values by the Intern-BM originates from the natural variations of biological tissues due to physiological processes or other functional requirements. De Santis [48] himself mentions a large variability of his results in his conclusion, however, lacks providing the standard deviation. The spread of the dielectric values from Gabriel et al. [45] used for the BM presented in this paper ranges from about ± 5–10% above 100 MHz to ± 15–25% at the lower end of the frequency scale [39]. Thus, our calculated values are within the statistically explainable deviation. The Intern-BM’s net impedance is therefore validated by the impedance measurements provided in the current literature.
The IT’IS tissue database does not consider the voltage dependency of the skin impedance at the contact area. Therefore, based upon the validated Intern-BM, the electrical properties of ZSkin needed to be found for the Total-BM. The deeply founded model of an RC circuit as ZSkin, as described in Section 2.3, was used to vary the electrical properties of its different elements for the best fitting model considering frequencies up to 1 kHz. The electrical properties of ZSkin shown in Table 2 led to compliance (cf. Total-BM in Fig. 3) with the impedance values derived from the IEC [1] for every chosen frequency between DC and 1 kHz. The results also comply with the general understanding on the capacitive properties of the skin for low voltages [46, 49]. The influence of the touch voltage is very large. The conductivity increases by a factor of 6 between 25 and 220 V touch voltage.
In general, the comparison of the total body impedance with literature values (cf. Fig. 3) confirms the validity of the net electrical tissue properties Intern-BM. The IEC [1] values additionally enable the validation of the voltage and frequency-dependent Total-BM, providing in return insights into the conductivity and relative permittivity of the skin under different exposure situations (cf. Table 2). Beside the skin, the electrical properties of other specific tissues are not directly assessable, but the agreement of the body models’ total body impedance with the literature is a clear indication that the individual tissue properties are also valid.
3.2 Numerical HCF of longitudinal current paths
Table 3 shows the numerical HCFs (FSamNum and F99Num as defined in method Section 2.6) determined in this study for xH-xF and PS-xH current paths. In this table, only the current paths which create longitudinal currents (current flowing lengthwise) in the trunk of the human body are shown. For comparison, FSam [19] HCF values that are the currently valid values provided in IEC 60479-1 [1] are shown in the second column. The HCFs are given from DC to 100 kHz as this is the spectrum for inducing VF. As defined in Section 2.6, the first row equals 1.0 because F99Num is normalized to the current path LH-BF for each frequency.
For the current paths shown in Table 3, the deviations of FSamNum and F99Num from 1.0 are negligible. They are also in accordance with the FSam values for the current paths LH-xF and BH-BF. For RH-xF and PS-xH current paths, however, F99Num and FSamNum deviate from the literature values [1].
The compliance of FSamNum with F99Num shows that the error due to the probe size in Sam’s method (described in Section 2.6) is not important for longitudinal current paths. Thus, for these current paths, the differences between Sam’s measurements and our numerical findings must be due to the differences of our numerical body model and the cadaver Sam used. A discussion about the quality of both approaches is necessary, because the IEC [1] results, which origin from Sam [19], have been accepted and applied in practice for decades. They should therefore not be dismissed easily.
Sam [19] explained the lower HCFs for RH-xF in comparison with the LH-xF with basic human anatomy. He suggests that the asymmetric position of the ventricles lead to this effect. Figure 4 indicates a reasonable explanation as to why the numerical body model reveals similar F99Num and FSamNum for all longitudinal current paths. In case of longitudinal currents, the current enters the heart lumen through the blood vessels (subclavian artery/vein, aorta, and vena cava; cf. Fig. 4 LH-BF black arrows) which are in the thorax center or symmetric to the median plane. The current is then driven into the heart lumen and through the heart muscle downwards to the feet/foot/seat. It enhances the EF in the heart muscle of, e.g., the right ventricle (cf. Fig. 4 *1) and is a major determinant of E99Heart and therefore F99Num. The described current-channeling effect is present at all longitudinal current paths (xH-xF and PS-xH) and only loses influence on F99Num at 100 kHz. At these higher frequencies, the heart’s offset to the left reduces F99Num of the RH and BH current paths (6% at maximum) in comparison to LH current paths and lower frequencies. This is due to the increased homogeneity of EF in the trunk at these frequencies (cf. Fig. 4, 100 kHz panels), which reduces the channeling effect.
Field distributions for the current paths LH-BF and LH-RH. The amplitude of the electric field E for 50 Hz (a) and 100 kHz (b) is shown from 0 (bright) to 30 dB (dark). The current density J for 50 Hz (c) and 100 kHz (d) is shown from 0 (bright) to 40 dB (dark). The black arrows show the current density direction and amplitude. Additional markers and highlights are explained in this section’s running text
Assuming the current-channeling effect was attenuated or not present during Sam’s [19] cadaver measurements, the anatomic asymmetry of the human heart would increase its influence on the HCF and explain the different results. There are some possible reasons why Sam did not recognize a current-channeling effect: The numerical body model used has no heart valves, which change the electrical conditions within the heart. Since the conductivity of the heart valves are lower than that of blood, closed heart valves could increase the impedance between the atria and the ventricles and thereby limit the current-channeling effect in a real human heart. Closed or incompletely open heart valves of the cadaver in Sam’s study would therefore lead to an underestimated HCF value. Likewise, the absence of the heart valve in the numerical body model could overestimate the HCF. The detection of impedance changes due to opening or closure of the heart valves is also being used in heart valve prosthesis [50].
A second explanation for the differences is connected to the conductivity of the blood. It is not, a priori, surprising that cadaver tissue properties should deviate, possibly significantly, from values of living tissue. The conductivity of the blood changes post mortem due to the coagulation process. Sam [23] performed his experiments on cadavers up to 17 h post mortem. According to Freiberger [13], the total body impedance increases rapidly in the first hours after death which might be a result of a decrease of the body temperature and tissue conductivites. Haemmerich et al. [51] considered the blood occlusion post mortem as the main reason for changes in conductivity and therefore also body impedance. A lower blood conductivity would also attenuate the current-channeling effect and could subsequently lead to an underestimation of the HCF. In the future, research simulations should be done with the body model by using post-mortem blood conductivity to prove this effect.
Additional research using body models with heart valves and comprehensive examinations of different blood conductivities could clarify to what extent the explanations hold for the differences of LH-xF vs. RH-xF longitudinal current paths. Nevertheless, the numerical model represents at least the worst-case approach for these current paths, if not the real case. It is therefore a significant addition to the current knowledge on HCFs.
3.3 Numerical HCF of transversal current paths
Table 4 is the continuation of Table 3 and shows the F99Num determined in this study for current paths (LH-RH, LF-RF, and xT-xH) which create a current flow across the trunk of the human body (transversal current).
In the path for Fig. 4, no obvious current channel is present for the LH-RH current path. The EF histograms in Fig. 5 confirm this impression. The distribution is much narrower for the LH-RH current path in comparison to LH-BF. This means a more homogenous EF distribution is created by the LH-RH current path. Consistently, the numerical imitation of Sam [19] (FSamNum) is in stronger accordance with Sam’s cadaver measurements (at 50 Hz) in transversal current paths than in longitudinal current paths. Meaning that, FSamNum and Sam’s [19] values both show the tendency of a higher HCF for xT-LH current paths and also comply in absolute values.
F99Num varies considerably among the various transversal current paths. For xT-xH current paths, F99Num depends extremely on the xT contact electrode position, due to the proximity of the electrode to the heart. The dependency was found because Sam [19] did not give specific anatomical description of his electrode placement and we therefore changed the electrodes’ positions in the range of 2 cm (any direction). The electrode position shown in Fig. 1 leads to the highest F99Num, which are presented in Table 4. Position adjustments in the range of 1–2 cm (any direction) can influence F99Num in the order of 0.5. Therefore, a safety margin should be added when using those F99Num, although the results are already exceeding the IEC [1] values up to 0.65 at 50 Hz. Scrutinizing the electrode position dependency of F99Num could contribute to VF assessment and research needs are hereby addressed.
The strong deviation between F99Num and FSamNum for AT-xH occurs because of the proximity of the electrode to the heart. This creates inhomogeneity of the EF within the myocardium. As described in the methods, a possible explanation for our results differences with respect to Sam’s original measurements may stem from the averaging effect due to the probe size (160 mm). Our results, therefore, should be further investigated and given special consideration in future risk assessments of AT-xH current paths.
3.4 HCF frequency dependency
The results for longitudinal current paths reveal nearly no influence of the frequency on the HCF (cf. Table 3). F99Num deviates 7% from 1.0 at maximum, between 50 Hz and 10 kHz the deviation is even smaller (3% at maximum). This indicates that the HCF for longitudinal current path is not frequency dependent.
For transversal current paths F99Num changes with the frequency, i.e., LH-RH F99Num increases by 0.16 and AT-LH F99Num increases by 0.21 from DC to 100 kHz. The main changes are noticeable between DC and 50 Hz and 10 kHz and 100 kHz. In contrast to the longitudinal current paths, no obvious current channels are visible in the trunk of the body model for the transversal current paths (e.g., cf. Fig. 4 LH-RH black arrows). The frequency dependency of F99Num is therefore most likely due to the increasing homogeneity of the EF in the trunk. As an example of that, the EF distribution in the ventricle myocardium is shown in Fig. 5 for the current paths LH-BF and LH-RH at 50 Hz and 100 kHz. At 100 kHz, the histograms are narrower than at 50 Hz, meaning that there is less variance in the distribution of the EF strength. Further it is noticeable that E99Heart decreases with the frequency for both current paths. E99Heart of LH-RH decreases less with the frequency in comparison with LH-BF and therefore, according to (2), F99Num increases with the frequency.
This new knowledge can be put into the context of the frequency dependency of the VF threshold, for example, given in IEC [14] and IEC [52]. The VF threshold rises roughly linearly with the frequency [53, 54]. This means that with increasing CC frequency, the myocardial cells are less sensitive. At CC frequencies above 100 kHz, myocardial tissue is therefore more likely to be burned before it is excited [8]. Note that cardiac ablation is routinely performed in humans using 500 kHz and rarely induces VF [8, 55]. Taking that into account IEC [15] introduced the so-called frequency factor, which allows higher CC amplitudes for higher frequencies. However, to date frequency-dependent HCF values have not been considered. The results of this study suggest frequency dependent HCFs for transverse current paths. For longitudinal current path, frequency correction seems not necessary.
4 Conclusion
This study presents computational methods for dosimetric studies on CCs by providing an extendable and adaptable body model. The developed model features validated total body impedances, considers skeletal muscle impedance anisotropy, and includes validated skin impedance models, which take the frequency and the touch voltage into account. Both validations were conducted using in vivo data presented in IEC 60479-1 [1] which was obtained by measurements on 100 living persons at 25 V AC 50 Hz in dry conditions with large surface areas of contact. Due to strong muscular effects, higher touch voltages (up to 200 V) were determined from only one human as the mean value of 6 measurements at each touch voltage [18]. Due to the extensive validation, the numeric body model described in this study is applicable to a wide range of accident scenarios. These accident scenarios could contain any frequency between DC and 1 MHz, smaller or bigger contact areas and different contact positions.
The developed skin model has the advantage of controlling the contact area size exactly and it controls the electrical skin properties at the contact area locally, which is necessary because these properties change locally in case of CCs. When using the skin model in further studies, it should be considered that here, the skin of the hands was used for the validation. Certain body areas might have thicker or thinner skin and therefore other electrical properties. The skin model was validated for contact dimensions of 10 cm. The derived conductivity and relative permittivity values, however, allow impedance estimations for smaller or bigger contact areas. In case of uncertainty concerning the skin properties, impedance measurements would be necessary to calculate an adapted skin model using the methods presented above.
The presented HCF assessment is one of the major applications for the body model. It helps to understand the risk dependence of VF on the CC path and frequency. The results reveal HCFs from DC to 100 kHz and show frequency-dependent HCFs for transversal current paths, which are not considered in current standards like IEC [15] so far. Additionally, the model enables HCF calculations for special applications where individual current paths are in question. The comparison of Sam’s cadaver study and the numerical approach revealed that the blood conductivity, the heart valves, and the myocardial anisotropy need to be further researched in order to evaluate their exact influence on the HCFs for longitudinal current paths. Until such, research is performed and published, the results presented by Sam and published by IEC 60479-1 shall continue being the guiding information for cardiac risk and for estimating heart factor values.
A second major application field for the developed model is the assessment of certain tissues or particular organs. In Fig. 4, the marker *2 shows the current density in the carotid arteries and jugular veins as being highly significant. Thus, brain current factors should be of interest in upcoming studies to explain injuries affecting the brain following electrical injuries [6]. The body models’ output datasets (electric field and current density) enable ICNIRP [20] and IEEE [21, 22] assessments for every current path and frequency from DC to 1 MHz.
References
IEC (2018) Effects of current on human beings and livestock - Part 1: General aspects (IEC 60479-1:2018). International electrotechnical commission. International Standard (2018-12)
Andrews CJ (2006) Further documentation of remote effects of electrical injuries, with comments on the place of neuropsychological testing and functional scanning. IEEE Trans Biomed Eng 53:2102–2113. https://doi.org/10.1109/TBME.2006.877117
Andrews CJ (2014) A Review of the Psychological Consequences of Lightning and Electrical Injury. Proc: 2014 International Conference on Lightning Protection, Shanghai, China
Breugem CC, Van Hertum W, Groenevelt F (1999) High voltage electrical injury leading to a delayed onset tetraplegia, with recovery. Ann N Y Acad Sci 888:131–136. https://doi.org/10.1111/j.1749-6632.1999.tb07950.x
Duff K, McCaffrey RJ (2001) Electrical injury and lightning injury: a review of their mechanisms and neuropsychological, psychiatric, and neurological sequelae. Neuropsychol Rev 11:101–116. https://doi.org/10.1023/A:1016623318049
Kurtulus A, Acar K, Adiguzel E, Boz B (2009) Hippocampal neuron loss due to electric injury in rats: a stereological study. Leg Med (Tokyo) 11:59–63. https://doi.org/10.1016/j.legalmed.2008.08.001
Park KH, Park WJ, Kim MK, Kim HS, Kim SH, Cho GY, Choi YJ (2012) Alterations in arterial function after high-voltage electrical injury. Crit Care 16:R25. https://doi.org/10.1186/cc11190
Ikeda T, Sugi K, Ninomiya K, Enjoji Y, Abe R, Yabuki S, Yamaguchi T (1993) Optimal frequency of radiofrequency catheter ablation in vitro and in vivo for treating ventricular tachycardias--a study using various frequencies. Jpn Circ J 57:921–927. https://doi.org/10.1253/jcj.57.921
Osypka P (1963) Messtechnische Untersuchungen über Stromstärke, Einwirkungsdauer und Stromweg bei elektrischen Wechselstromunfällen an Mensch und Tier. Bedeutung und Auswertung für Starkstromanlagen. (Metrological investigation in humans and animals on amplitude, exposure time and pathway in AC electric current accidents part 1). Elektromedizin und ihre Grenzgebiete 8:153–179
Dalziel CF (1972) Electric shock hazard. IEEE Spectr 9:41–50. https://doi.org/10.1109/MSPEC.1972.5218692
Dalziel CF, Lee WR (1968) Reevaluation of lethal electric currents. IEEE Trans Ind Appl 4:467–476. https://doi.org/10.1109/TIGA.1968.4180929
Dalziel CF, Lee WR (1969) Lethal electric currents. IEEE Spectr 6:44–50. https://doi.org/10.1109/MSPEC.1969.5213962
Freiberger H (1934) Der elektrische Widerstand des menschlichen Körpers gegen technischen Gleich- und Wechselstrom. (the electrical resistance of the human body against technical direct and alternating current). Dr. Ing. Doctoral thesis Technische Hochschule Berlin (in German),
IEC (2019) Effects of current on human beings and livestock - Part 2: Special aspects (IEC 60479-2:2019). International electrotechnical commission. International Standard (2019-05)
IEC (2007) Effects of current on human beings and livestock - part 5: touch voltage threshold values for physiological effects. IEC/TR 60479-5:2007–2011
IEC (2020) Effects of current on human beings and livestock - Part 4: effects of lightning strokes. IEC TR 60479-4:2020
Biegelmeier G, Bachl H, Moerx A, Rabitsch G (1991) Neue Messungen des Koerperwiderstandes lebender Menschen mit Wechselstrom 50 Hz, sowie mit hoeheren Frequenzen und mit Gleichstrom. (in German: New measurements of body resistance of living people with alternating current 50 Hz, as well as with higher frequencies and with direct current). e&i 108(3):96–113
Biegelmeier G, Hönninger E, Küttner J, Miksch J, Schuy S (1979) Über Messungen des elektrischen Widerstandes der Körper lebender menschen in Zusammenhang mit Normungsfragen bei den Schutzmassnahmen gegen elektrische Unfälle in Niederspannungsanlagen. (on measurements of the electrical resistance of the bodies of living people in connection with standardization issues concerning protective measures against electrical accidents in low voltage installations). E und M 96:53–61
Sam U (1967) Untersuchungen über die elektrische Gefährdung des Menschen bei Teildurchströmungen, insbesondere bei Arbeiten in Kesseln, Behältern und Rohrleitungen (2. Teil). (Investigations into the electrical hazard to humans in the event of partial flow, in particular during work in boilers, containers and pipelines (2nd part)). Elektromed Biomed Tech 12:29–37. https://doi.org/10.1515/bmte.1967.12.1-6.29
ICNIRP (2010) Guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz to 100 kHz). Health Phys 99:818–836. https://doi.org/10.1097/HP.0b013e3181f06c86
IEEE (2018) IEEE Standard for Radio-Frequency Energy and Current-Flow Symbols (C95.2-2018). IEEE International Committee on Electromagnetic Safety (2018-10)
IEEE (2019) IEEE Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic, and Electromagnetic Fields, 0 Hz to 300 GHz (C95.1-2019). IEEE International Committee on Electromagnetic Safety (2019-02). https://doi.org/10.1109/IEEESTD.2019.8859679
Sam U (1966) Untersuchungen über die elektrische Gefährdung des menschen bei Teildurchströmungen, insbesondere bei Arbeiten in Kesseln, Behältern und Rohrleitungen (1. Teil). (investigations into the electrical hazard to humans in the event of partial flow, in particular during work in boilers, containers and pipelines (1st part)). Elektromed Biomed Tech 11:193–212
Brucher R, Friedmann B, Mayer-Waarden K (1983) Berechnung eines dreidimensionalen, elektrischen Feldes bei einer realen Gewebeverteilung des biologischen mediums (calculation of a three dimensional electric field using real tissue positioning of the biological medium). Biomed Tech (Berl) 28:203–204 (in German)
Brucher R, Mayer-Waarden K (1984) Ermittlung der mittleren gefährlichen Gesamtstromstärken bei elektrischer Durchströmung des Menschen mittels dreidimensionaler, numerischer Berechnungen in einem aus computertomographischen Daten erstellten Modell (Risk assessment of body currents due to electric shocks using three dimensional numerical calculations on CAT scan data). Biomed Tech (Berl) 29:203–204 (in German)
Brucher R, Mayer-Waarden K (1985) Rechnergestützte Ermittlung gefährlicher Gesamtströme im menschlichen Körper (computer-aided determination of hazardous total flows in the human body). Inst zur Erforschung Elektr, Unfälle
Biegelmeier G, Kieback D, Kiefer G, Krefter K-H (2003) Schutz in elektrischen Anlagen - Band 1: Gefahren durch den elektrischen Strom (Protection in electrical installations - Volume 1: Electrical current hazards). In: VDE-Schriftenreihe Normen verständlich, 2nd edn. VDE Verlag GmbH, Berlin
Chan KH, Hattori J, Laakso I, Hirata A, Taki M (2013) Computational dosimetry for grounded and ungrounded human models due to contact current. Phys Med Biol 58:5153–5172. https://doi.org/10.1088/0031-9155/58/15/5153
Chan KH, Ohta S, Laakso I, Hirata A, Suzuki Y, Kavet R (2015) Computational dosimetry for child and adult human models due to contact current from 10 Hz to 110 MHz. Radiat Prot Dosim 167:642–652. https://doi.org/10.1093/rpd/ncu322
Tarao H, Kuisti H, Korpinen L, Hayashi N, Isaka K (2012) Effects of tissue conductivity and electrode area on internal electric fields in a numerical human model for ELF contact current exposures. Phys Med Biol 57:2981–2996. https://doi.org/10.1088/0031-9155/57/10/2981
Dawson TW, Caputa K, Stuchly MA, Kavet R (2001) Electric fields in the human body resulting from 60-Hz contact currents. IEEE Trans Biomed Eng 48:1020–1026. https://doi.org/10.1109/10.942592
Freschi F, Guerrisi A, Tartaglia M, Mitolo M (2012) Numerical simulation of heart-current factors and electrical models of the human body. 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA. https://doi.org/10.1109/IAS.2012.6374099
Reilly JP, Hirata A (2016) Low-frequency electrical dosimetry: research agenda of the IEEE International Committee on Electromagnetic Safety. Phys Med Biol 61:R138–R149. https://doi.org/10.1088/0031-9155/61/12/R138
Christ A, Kainz W, Hahn EG, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B, Schmitt P, Hollenbach HP, Shen J, Oberle M, Szczerba D, Kam A, Guag JW, Kuster N (2010) The virtual family-development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol 55:N38. https://doi.org/10.1088/0031-9155/55/2/N01
Epstein BR, Foster KR (1983) Anisotropy in the dielectric properties of skeletal muscle. Med Biol Eng Comput 21:51–55. https://doi.org/10.1007/BF02446406
Hasgall PA, Di Gennaro F, Baumgartner C, Neufeld E, Lloyd B, Gosselin MC, Payne D, Klingenböck A, Kuster N (2018) IT'IS Database for thermal and electromagnetic parameters of biological tissues. itis.swiss/database. Accessed December 16, 2019
Gabriel C, Gabriel S, Corthout E (1996) The dielectric properties of biological tissues: I. Literature survey. Phys Med Biol 41:2231–2249. https://doi.org/10.1088/0031-9155/41/11/001
Gabriel C, Peyman A, Grant EH (2009) Electrical conductivity of tissue at frequencies below 1 MHz. Phys Med Biol 54:4863–4878. https://doi.org/10.1088/0031-9155/54/16/002
Gabriel S, Lau RW, Gabriel C (1996) The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol 41:2251–2269. https://doi.org/10.1088/0031-9155/41/11/002
Gabriel S, Lau RW, Gabriel C (1996) The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol 41:2271–2293. https://doi.org/10.1088/0031-9155/41/11/003
Dawson TW, Stuchly MA (1998) Effects of skeletal muscle anisotropy on human organ dosimetry under 60 Hz uniform magnetic field exposure. Phys Med Biol 43:1059–1074. https://doi.org/10.1088/0031-9155/43/5/002
Tachas NJ, Samaras T, Baskourelos K, Sahalos JN (2009) Effects of skeletal muscle anisotropy on induced currents from low-frequency magnetic fields. Phys Med Biol 54:N541–N547. https://doi.org/10.1088/0031-9155/54/23/N02
IEC (2016) Methods of measurement of touch current and protective conductor current (IEC 60990:2016-05). International electrotechnical commission. International Standard (2016-05)
Panescu D, Cohen KP, Webster JG, Stratbucker RA (1993) The mosaic electrical characteristics of the skin. IEEE Trans Biomed Eng 40:434–439. https://doi.org/10.1109/10.243418
Gabriel C (1996) Compilation of the dielectric properties of body tissues at RF and microwave frequencies
Lawler JC, Davis MJ, Griffith EC (1960) Electrical characteristics of the skin. The impedance of the surface sheath and deep tissues. J Invest Dermatol 34:301–308. https://doi.org/10.1038/jid.1960.52
Chatterjee I, Wu D, Gandhi OP (1986) Human body impedance and threshold currents for perception and pain for contact hazard analysis in the VLFMF band. IEEE Trans Biomed Eng 33:486–494. https://doi.org/10.1109/TBME.1986.325735
De Santis V, Beeckman PA, Lampasi DA, Feliziani M (2011) Assessment of human body impedance for safety requirements against contact currents for frequencies up to 110 MHz. IEEE Trans Biomed Eng 58:390–396. https://doi.org/10.1109/TBME.2010.2066273
Panescu D, Webster JG, Stratbucker RA (1994) A nonlinear electrical-thermal model of the skin. IEEE Trans Biomed Eng 41:672–680. https://doi.org/10.1109/10.301734
Marcelli E, Bortolani B, Corazza I, Cercenelli L (2018) A novel sensorized heart valve prosthesis: preliminary in vitro evaluation. Sensors 18:3905. https://doi.org/10.3390/s18113905
Haemmerich D, Ozkan OR, Tsai J-Z, Staelin ST, Tungjitkusolmun S, Mahvi DM, Webster JG (2002) Changes in electrical resistivity of swine liver after occlusion and postmortem. Med Biol Eng Comput 40:29–33. https://doi.org/10.1007/BF02347692
IEC (2020) Medical electrical equipment - Part 1: General requirements for basic safety and essential performance - Collateral Standard: Requirements for environmentally conscious design (IEC 60601-1-9:2007+A1:2013+A2:2020). International electrotechnical commission. International Standard (2020-07)
Geddes LA, Baker LE, Moore AG, Coulter TW (1969) Hazards in the use of low frequencies for the measurement of physiological events by impedance. Med & biol Engng 7:289–296. https://doi.org/10.1007/BF02474769
Malkin RA, de Jongh CA (2003) Frequency dependence of the cardiac threshold to alternating current between 10 Hz and 160 Hz. Med Biol Eng Comput 41:640–645. https://doi.org/10.1007/bf02349971
Potse M, Essebag V (2009) Guidance for catheter ablation of ventricular arrhythmia. Med Biol Eng Comput 47:241–243. https://doi.org/10.1007/s11517-008-0428-6
Funding
Open Access funding enabled and organized by Projekt DEAL. This study was funded by the German Social Accident Insurance Institution for the Energy, Textile, Electrical, and Media Products Sectors (BG ETEM).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Data availability statement
The datasets generated and analyzed during the study are available from the corresponding author on reasonable request.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schneeweiss, P., Panescu, D., Stunder, D. et al. Computational models for contact current dosimetry at frequencies below 1 MHz. Med Biol Eng Comput 59, 107–119 (2021). https://doi.org/10.1007/s11517-020-02284-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-020-02284-9