Skip to main content
SpringerLink
Log in

Effective models for nearly ideal Dirac semimetals

  • Research Article
  • Published:
Frontiers of Physics Aims and scope Submit manuscript

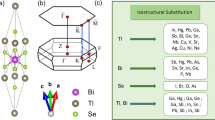
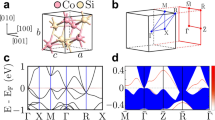
Abstract

Topological materials (TMs) have gained intensive attention due to their novel behaviors compared with topologically trivial materials. Among various TMs, Dirac semimetal (DSM) has been studied extensively. Although several DSMs have been proposed and verified experimentally, the suitable DSM for realistic applications is still lacking. Thus finding ideal DSMs and providing detailed analyses to them are of both fundamental and technological importance. Here, we sort out 8 (nearly) ideal DSMs from thousands of topological semimetals in Nature 566(7745), 486 (2019). We show the concrete positions of the Dirac points in the Brillouin zone for these materials and clarify the symmetry-protection mechanism for these Dirac points as well as their low-energy effective models. Our results provide a useful starting point for future study such as topological phase transition under strain and transport study based on these effective models. These DSMs with high mobilities are expected to be applied in fabrication of functional electronic devices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Klitzing, G. Dorda, and M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45(6), 494 (1980)

    Article  ADS  Google Scholar 

  2. D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Quantized Hall conductance in a two-dimensional periodic potential, Phys. Rev. Lett. 49(6), 405 (1982)

    Article  ADS  Google Scholar 

  3. M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators, Rev. Mod. Phys. 82(4), 3045 (2010)

    Article  ADS  Google Scholar 

  4. X. L. Qi and S. C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83(4), 1057 (2011)

    Article  ADS  Google Scholar 

  5. Y. Ando and L. Fu, Topological crystalline insulators and topological superconductors: From concepts to materials, Annu. Rev. Condens. Matter Phys. 6(1), 361 (2015)

    Article  ADS  Google Scholar 

  6. N. P. Armitage, E. J. Mele, and A. Vishwanath, Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys. 90(1), 015001 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  7. T. O. Wehling, A. M. Black-Schaffer, and A. V. Balatsky, Dirac materials, Adv. Phys. 63(1), 1 (2014)

    Article  ADS  Google Scholar 

  8. S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele, and A. M. Rappe, Dirac semimetal in three dimensions, Phys. Rev. Lett. 108(14), 140405 (2012)

    Article  ADS  Google Scholar 

  9. Z. Wang, Y. Sun, X. Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai, and Z. Fang, Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb), Phys. Rev. B 85(19), 195320 (2012)

    Article  ADS  Google Scholar 

  10. Z. Wang, H. Weng, Q. Wu, X. Dai, and Z. Fang, Three-dimensional Dirac semimetal and quantum transport in Cd3As2, Phys. Rev. B 88(12), 125427 (2013)

    Article  ADS  Google Scholar 

  11. Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S. K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain, and Y. L. Chen, Discovery of a three-dimensional topological Dirac semimetal, Na3Bi, Science 343(6173), 864 (2014)

    Article  ADS  Google Scholar 

  12. Z. K. Liu, J. Jiang, B. Zhou, Z. J. Wang, Y. Zhang, H. M. Weng, D. Prabhakaran, S.-K. Mo, H. Peng, P. Dudin6, T. Kim, M. Hoesch, Z. Fang, X. Dai, Z. X. Shen, D. L. Feng, Z. Hussain, and Y. L. Chen, A stable three-dimensional topological Dirac semimetal Cd3As2, Nat. Mater. 13, 677C681 (2014)

    Google Scholar 

  13. B. J. Yang and N. Nagaosa, Classification of stable three-dimensional Dirac semimetals with nontrivial topology, Nat. Commun. 5(1), 4898 (2014)

    Article  ADS  Google Scholar 

  14. M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, Chiral tunnelling and the Klein paradox in graphene, Nat. Phys. 2(9), 620 (2006)

    Article  Google Scholar 

  15. M. Yan, H. Huang, K. Zhang, E. Wang, W. Yao, K. Deng, G. Wan, H. Zhang, M. Arita, H. Yang, Z. Sun, H. Yao, Y. Wu, S. Fan, W. Duan, and S. Zhou, Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2, Nat. Commun. 8(1), 257 (2017)

    Article  ADS  Google Scholar 

  16. H. J. Noh, J. Jeong, E. J. Cho, K. Kim, B. I. Min, and B. G. Park, Experimental realization of type-II Dirac fermions in a PdTe2 superconductor, Phys. Rev. Lett. 119(1), 016401 (2017)

    Article  ADS  Google Scholar 

  17. F. Fei, X. Bo, R. Wang, B. Wu, J. Jiang, D. Fu, M. Gao, H. Zheng, Y. Chen, X. Wang, H. Bu, F. Song, X. Wan, B. Wang, and G. Wang, Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2, Phys. Rev. B 96(4), 041201 (2017)

    Article  ADS  Google Scholar 

  18. Q. D. Gibson, L. M. Schoop, L. Muechler, L. S. Xie, M. Hirschberger, N. P. Ong, R. Car, and R. J. Cava, Three-dimensional Dirac semimetals: Design principles and predictions of new materials, Phys. Rev. B 91(20), 205128 (2015)

    Article  ADS  Google Scholar 

  19. Q. S. Wu, C. Piveteau, Z. Song, and O. V. Yazyev, MgTa2N3: A reference Dirac semimetal, Phys. Rev. 98, 081115(R) (2018)

    Article  Google Scholar 

  20. W. D. Cao, P. Z. Tang, S.-C. Zhang, W. H. Duan, and A. Rubio, Stable Dirac semimetal in the allotropes of group-IV elements, Phys. Rev. B 93, 241117(R) (2016)

    Article  ADS  Google Scholar 

  21. X. Zhang, Q. Liu, Q. Xu, X. Dai, and A. Zunger, Topological insulators versus topological Dirac semimetals in honeycomb compounds, J. Am. Chem. Soc. 140(42), 13687 (2018)

    Article  Google Scholar 

  22. X. L. Sheng, Z. Wang, R. Yu, H. Weng, Z. Fang, and X. Dai, Topological insulator to Dirac semimetal transition driven by sign change of spin-orbit coupling in thallium nitride, Phys. Rev. B 90(24), 245308 (2014)

    Article  ADS  Google Scholar 

  23. Y. Du, B. Wan, D. Wang, L. Sheng, C. G. Duan, and X. Wan, Dirac and Weyl semimetal in XYBi (X = Ba, Eu; Y = Cu, Ag and Au), Sci. Rep. 5(1), 14423 (2015)

    Article  ADS  Google Scholar 

  24. Y. P. Du, F. Tang, D. Wang, L. Sheng, E. J. Kan, C.-G. Duan, S. Y. Savrasov, and X. G. Wan, CaTe: A new topological node-line and Dirac semimetal, npj Quant. Mater. 2, 3 (2017)

    Article  ADS  Google Scholar 

  25. R. Chen, H. C. Po, J. B. Neaton, and A. Vishwanath, Topological materials discovery using electron filling constraints, Nat. Phys. 14(1), 55 (2018)

    Article  Google Scholar 

  26. T. Zhang, Y. Jiang, Z. Song, H. Huang, Y. He, Z. Fang, H. Weng, and C. Fang, Catalogue of topological electronic materials, Nature 566(7745), 475 (2019)

    Article  ADS  Google Scholar 

  27. M. G. Vergniory, L. Elcoro, C. Felser, N. Regnault, B. A. Bernevig, and Z. Wang, A complete catalogue of high-quality topological materials, Nature 566(7745), 480 (2019)

    Article  ADS  Google Scholar 

  28. F. Tang, H. C. Po, A. Vishwanath, and X. Wan, Comprehensive search for topological materials using symmetry indicators, Nature 566(7745), 486 (2019)

    Article  ADS  Google Scholar 

  29. J. Xiong, S. K. Kushwaha, T. Liang, J. W. Krizan, M. Hirschberger, W. Wang, R. J. Cava, and N. P. Ong, Evidence for the chiral anomaly in the Dirac semimetal Na3Bi, Science 350(6259), 413 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. M. Neupane, S. Y. Xu, R. Sankar, N. Alidoust, G. Bian, C. Liu, I. Belopolski, T. R. Chang, H. T. Jeng, H. Lin, A. Bansil, F. Chou, and M. Z. Hasan, Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2, Nat. Commun. 5(1), 3786 (2014)

    Article  ADS  Google Scholar 

  31. H. C. Po, A. Vishwanath, and H. Watanabe, Symmetry-based indicators of band topology in the 230 space groups, Nat. Commun. 8(1), 50 (2017)

    Article  ADS  Google Scholar 

  32. F. Tang, H. C. Po, A. Vishwanath, and X. Wan, Efficient topological materials discovery using symmetry indicators, Nat. Phys. 15, 470 (2019)

    Article  Google Scholar 

  33. O. Muller and R. Roy, Synthesis and crystal chemistry of some new complex palladium oxides, Adv. Chem. Ser. 98, 28 (1971)

    Article  Google Scholar 

  34. P. Norby, R. E. Dinnebier, and A. N. Fitch, Decomposition of silver carbonate: the crystal structure of two high-temperature modifications of Ag2CO3, Inorg. Chem. 41(14), 3628 (2002)

    Article  Google Scholar 

  35. C. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids, Oxford: Claredon Press, 1972

    MATH  Google Scholar 

  36. O. Graudejus and B. G. Mueller, Ag2+ in trigonalbipyramidaler Umgebung: Neue Fluoride mit zweiwertigem Silber: Ag M(II)3 M(IV)3 F20 (M(II) = Cd, Ca, Hg; M(IV) = Zr, Hf), Zeitschrift fuer Anorganische und Allgemeine Chemie (1950) (DE) 622, 1549–1556 (1996)

    Article  Google Scholar 

  37. T. Yamada, V. L. Deringer, R. Dronskowski, and H. Yamane, Synthesis, crystal structure, chemical bonding, and physical properties of the ternary Na/Mg stannide, Na2MgSn, Inorg. Chem. 51(8), 4810 (2012)

    Article  Google Scholar 

  38. B. Peng, C. M. Yue, H. Zhang, Z. Fang, and H. M. Weng, Predicting Dirac semimetals based on sodium ternary compounds, npj Comput. Mater. 4, 68 (2018)

    Article  ADS  Google Scholar 

  39. H. Zentgraf, K. Claes, and R. Hoppe, Oxide eines neuen Formeltyps: Zur Kenntnis von K3Ni2O4 und K3Pt2O4, Zeitschrift fuer Anorganische und Allgemeine Chemie (1950) (DE) 462, 92–105 (1980)

    Article  Google Scholar 

  40. Z. Nong, J. Zhu, X. Yang, Y. Cao, Z. Lai, and Y. Liu, The mechanical, thermodynamic and electronic properties of Al3Nb with DO22 structure: A first-principles study, Physica B 407(17), 3555 (2012)

    Article  ADS  Google Scholar 

  41. H. He, C. Tyson, and S. Bobev, Eight-coordinated arsenic in the Zintl phases RbCd4As3 and RbZn4As3: Synthesis and structural characterization, Inorg. Chem. 50(17), 8375 (2011)

    Article  Google Scholar 

  42. R. W. Henning and J. D. Corbett, Cs8Ga11, a new isolated cluster in a binary gallium compound: A family of valence analogues A8Tr11X: A = Cs, Rb; Tr = Ga, In, Tl; X = Cl, Br, I, Inorg. Chem. 36(26), 6045 (1997)

    Article  Google Scholar 

  43. P. Blaha, K. Schwarz, G. Madsen, D. Kvasicka, and J. Luitz, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, 2001

  44. J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77(18), 3865(1996)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 11525417, 11834006, 51721001, and 11790311) and the National Key R&D Program of China (Nos. 2018YFA0305704 and 2017YFA0303203).

Author information

Authors and Affiliations

  1. National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing, 210093, China

    Feng Tang & Xiangang Wan

  2. Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, 210093, China

    Feng Tang & Xiangang Wan

Authors
  1. Feng Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiangang Wan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiangang Wan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, F., Wan, X. Effective models for nearly ideal Dirac semimetals. Front. Phys. 14, 43603 (2019). https://doi.org/10.1007/s11467-019-0902-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11467-019-0902-7

Keywords

Search

Navigation