Skip to main content
SpringerLink
Log in

Synchronization of coupled metronomes on two layers

  • Research article
  • Published:
Frontiers of Physics Aims and scope Submit manuscript

Abstract

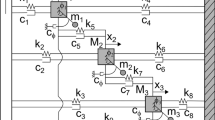
Coupled metronomes serve as a paradigmatic model for exploring the collective behaviors of complex dynamical systems, as well as a classical setup for classroom demonstrations of synchronization phenomena. Whereas previous studies of metronome synchronization have been concentrating on symmetric coupling schemes, here we consider the asymmetric case by adopting the scheme of layered metronomes. Specifically, we place two metronomes on each layer, and couple two layers by placing one on top of the other. By varying the initial conditions of the metronomes and adjusting the friction between the two layers, a variety of synchronous patterns are observed in experiment, including the splay synchronization (SS) state, the generalized splay synchronization (GSS) state, the anti-phase synchronization (APS) state, the in-phase delay synchronization (IPDS) state, and the in-phase synchronization (IPS) state. In particular, the IPDS state, in which the metronomes on each layer are synchronized in phase but are of a constant phase delay to metronomes on the other layer, is observed for the first time. In addition, a new technique based on audio signals is proposed for pattern detection, which is more convenient and easier to apply than the existing acquisition techniques. Furthermore, a theoretical model is developed to explain the experimental observations, and is employed to explore the dynamical properties of the patterns, including the basin distributions and the pattern transitions. Our study sheds new lights on the collective behaviors of coupled metronomes, and the developed setup can be used in the classroom for demonstration purposes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. Kuramoto, Chemical Oscillations, Waves and Turbulence, Berlin: Springer-Verlag, 1984

    Book  MATH  Google Scholar 

  2. A. S. Pikovsky, M. G. Rosenblum, and J. Kurths, Synchronization: A Universal Concept in Nonlinear Science, Cambridge: Cambridge University Press, 2001

    Book  MATH  Google Scholar 

  3. S. Strogatz, Sync: The Emerging Science of Spontaneous Order, New York: Hyperion, 2003

    Google Scholar 

  4. C. Huygens, [Letter to de Sluse]. Oeuveres Completes de Christian Huygens. (Letters; No. 133 of 24 February 1665, No. 1335 of 26 February 1665, No. 1345 of 6 March 1665), Societe Hollandaise DesSciences, Martinus Nijhor, La Haye, 1665

  5. M. Kapitaniak, K. Czolczynski, P. Perlikowski, A. Stefanski, and T. Kapitaniak, Synchronization of clocks, Phys. Rep. 517(1–2), 1 (2012)

    Article  ADS  MATH  Google Scholar 

  6. S. Boccaletti, J. Kurths, G. Osipov, D. L. Valladares, and C. S. Zhou, The synchronization of chaotic systems, Phys. Rep. 366(1–2), 1 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, and D. U. Hwang, Complex networks: Structure and dynamics, Phys. Rep. 424(4–5), 175 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  8. A. Arenas, A. Diaz-Guilera, J. Kurths, Y. Moreno, and C. S. Zhou, Synchronization in complex networks, Phys. Rep. 469(3), 93 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  9. C. Q. Wang, A. Pumir, N. B. Garnier, and Z. H. Liu, Explosive synchronization enhances selectivity: Example of the cochlea, Front. Phys. 12(5), 128901 (2017)

    Article  Google Scholar 

  10. S. F. Ma, H. J. Bi, Y. Zou, Z. H. Liu, and S. G. Guang, Shuttle-run synchronization in mobile ad hoc networks, Front. Phys. 10(3), 100505 (2015)

    Google Scholar 

  11. M. Bennett, M. F. Schatz, H. Rockwood, and K. Wiesenfeld, Huygens’s clocks, Proc. R. Soc. Lond. A 458(2019), 563 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. J. Pantaleone, Synchronization of metronomes, Am. J. Phys. 70(10), 992 (2002)

    Article  ADS  Google Scholar 

  13. Y. Wu, N. Wang, L. Li, and J. Xiao, Anti-phase synchronization of two coupled mechanical metronomes, Chaos 22(2), 023146 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Y. Wu, Z. Song, W. Liu, J. Jia, and J. Xiao, Experimental and numerical study on the basin stability of the coupled metronomes, Eur. Phys. J. Spec. Top. 223(4), 697 (2014)

    Article  Google Scholar 

  15. Z. Song, Y. Wu, W. Liu, and J. Xiao, Experimental study of the irrational phase synchronization of coupled nonidentical mechanical metronomes, PLoS One 10, 0118986 (2015)

    Google Scholar 

  16. Q. Hu, W. Liu, H. Yang, J. Xiao, and X. Qian, Experimental study on synchronization of three coupled mechanical metronomes, Eur. J. Phys. 34(2), 291 (2013)

    Article  Google Scholar 

  17. J. Jia, Z. Song, W. Liu, J. Kurths, and J. Xiao, Experimental study of the triplet synchronization of coupled nonidentical mechanical metronomes, Sci. Rep. 5, 17008 (2015)

    Article  ADS  Google Scholar 

  18. B. Kralemann, A. Pikovsky, and M. Rosenblum, Detecting triplet locking by triplet synchronization indices, Phys. Rev. E 87(5), 052904 (2013)

    Article  ADS  Google Scholar 

  19. K. Czolczynski, P. Perlikowski, A. Stefanski, and T. Kapitaniak, Clustering and synchronization of n Huygens’ clocks, Physica A 388(24), 5013 (2009)

    Article  ADS  MATH  Google Scholar 

  20. H. Ulrichs, A. Mann, and U. Parlitz, Synchronization and chaotic dynamics of coupled mechanical metronomes, Chaos 19(4), 043120 (2009)

    Article  ADS  Google Scholar 

  21. E. A. Martens, S. Thutupalli, A. Fourriere, and O. Hallatschek, Chimera states in mechanical oscillator networks, Proc. Natl. Acad. Sci. USA 110(26), 10563 (2013)

    Article  ADS  Google Scholar 

  22. S. Boda, S. Ujv’ari, A. Tunyagi, and Z. N’eda, Kuramoto-type phase transition with metronomes, Eur. J. Phys. 34(6), 1451 (2013)

    Article  Google Scholar 

  23. T. Kapitaniak, P. Kuzma, J. Wojewoda, K. Czolczynski, and Y. Maistrenko, Imperfect chimera states for coupled pendulums, Sci. Rep. 4, 6379 (2014)

    Article  ADS  Google Scholar 

  24. M. Hasler, Yu. Maistrenko, and O. Popovych, Simple example of partial synchronizaiton of chaotic systems, Phys. Rev. E 58(5), 6843 (1998)

    Article  ADS  Google Scholar 

  25. Y. Zhang, G. Hu, H. A. Cerdeira, S. Chen, T. Braun, and Y. Yao, Partial synchronization and spontaneous spatial ordering in coupled chaotic systems, Phys. Rev. E 63(2), 026211 (2001)

    Article  ADS  Google Scholar 

  26. D. M. Abrams and S. H. Strogatz, Chimera states for coupled oscillators, Phys. Rev. Lett. 93(17), 174102 (2004)

    Article  ADS  Google Scholar 

  27. C. Fu, Z. Deng, L. Huang, and X. G. Wang, Topological control of synchronous patterns in systems of networked chaotic oscillators, Phys. Rev. E 87(3), 032909 (2013)

    Article  ADS  Google Scholar 

  28. C. Fu, W. Lin, L. Huang, and X. G. Wang, Synchronization transition in networked chaotic oscillators: The viewpoint from partial synchronization, Phys. Rev. E 89(5), 052908 (2014)

    Article  ADS  Google Scholar 

  29. L. M. Pecora, F. Sorrentino, A. M. Hagerstrom, T. E. Murphy, and R. Roy, Cluster synchronization and isolated desynchronization in complex networks with symmetries, Nat. Commun. 5, 4079 (2014)

    Article  ADS  Google Scholar 

  30. T. Nishikawa and A. E. Motter, Symmetric states requiring system asymmetry, Phys. Rev. Lett. 117(11), 114101 (2016)

    Article  ADS  Google Scholar 

  31. M. Zhan, G. Hu, Y. Zhang, and D. He, Generalized splay state in coupled chaotic oscillators induced by weak mutual resonant interactions, Phys. Rev. Lett. 86(8), 1510 (2001)

    Article  ADS  Google Scholar 

  32. X. G. Wang, M. Zhan, C. H. Lai, and G. Hu, Measure synchronization in coupled j4 Hamiltonian systems, Phys. Rev. E 67(6), 066215 (2003)

    Article  ADS  Google Scholar 

  33. K. Czołczyński, P. Perlikowski, A. Stefańki, and T. Kapitaniak, Clustering of non-identical clocks, Prog. Theor. Phys. 125(3), 473 (2011)

    Article  ADS  MATH  Google Scholar 

  34. X. G. Wang, Y. C. Lai, and C. H. Lai, Enhancing synchronization based on complex gradient networks, Phys. Rev. E 75(5), 056205 (2007)

    Article  ADS  Google Scholar 

  35. X. G. Wang, L. Huang, Y. C. Lai, and C. H. Lai, Optimization of synchronization in gradient clustered networks, Phys. Rev. E 76(5), 056113 (2007)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 11375109, and also by the Fundamental Research Funds for the Central Universities under Grant No. GK201601001.

Author information

Authors and Affiliations

  1. School of Physics and Information Technology, Shaanxi Normal University, Xi’an, 710062, China

    Jing Zhang, Yi-Zhen Yu & Xin-Gang Wang

Authors
  1. Jing Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Zhen Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xin-Gang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yi-Zhen Yu or Xin-Gang Wang.

Additional information

arXiv: 1703.07936.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Yu, YZ. & Wang, XG. Synchronization of coupled metronomes on two layers. Front. Phys. 12, 120508 (2017). https://doi.org/10.1007/s11467-017-0675-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11467-017-0675-9

Keywords

PACS numbers

Search

Navigation