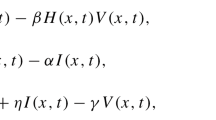Skip to main content
SpringerLink
Log in

A viral propagation model with a nonlinear infection rate and free boundaries

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

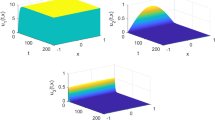
In this paper we put forward a viral propagation model with a nonlinear infection rate and free boundaries and investigate the dynamical properties. This model is composed of two ordinary differential equations and one partial differential equation, in which the spatial range of the first equation is the whole space ℝ, and the last two equations have free boundaries. As a new mathematical model, we prove the existence, uniqueness and uniform estimates of the global solution, and provide the criteria for spreading and vanishing, and the long time behavior of the solution components u, v and w. Comparing this model with the corresponding ordinary differential systems, the basic reproduction number \({{\cal R}_0}\) plays a different role. We find that when \({{\cal R}_0} \le 1\), the virus cannot spread successfully; when \({{\cal R}_0} > 1\), the successful spread of virus depends on the initial value and varying parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahn I, Baek S, Lin Z G. The spreading fronts of an infective environment in a man-environment-man epidemic model. Appl Math Model, 2016, 40: 7082–7101

    Article  MathSciNet  Google Scholar 

  2. Bunting G, Du Y H, Krakowski K. Spreading speed revisited: Analysis of a free boundary model. Netw Heterog Media, 2012, 42: 583–603

    Article  MathSciNet  Google Scholar 

  3. Capasso V, Maddalena L. Convergence to equilibrium states for a reaction-diffusion system modelling the spatial spread of a class of bacterial and viral diseases. J Math Biol, 1981, 13: 173–184

    Article  MathSciNet  Google Scholar 

  4. Du Y H, Lin Z G. Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary. SIAM J Math Anal, 2010, 42: 377–405

    Article  MathSciNet  Google Scholar 

  5. Du Y H, Lin Z G. The diffusive competition model with a free boundary: Invasion of a superior or inferior competitor. Discrete Contin Dyn Syst Ser B, 2014, 19: 3105–3132

    MathSciNet  MATH  Google Scholar 

  6. Du Y H, Ma L. Logistic type equations on ℝN by a squeezing method involving boundary blow-up solutions. J Lond Math Soc (2), 2001, 64: 107–124

    Article  MathSciNet  Google Scholar 

  7. Du Y H, Wang M X, Zhou M L. Semi-wave and spreading speed for the diffusive competition model with a free boundary. J Math Pures Appl (9), 2017, 107: 253–287

    Article  MathSciNet  Google Scholar 

  8. Guo J S, Wu C H. On a free boundary problem for a two-species weak competition system. J Dynam Differential Equations, 2012, 24: 873–895

    Article  MathSciNet  Google Scholar 

  9. Guo J S, Wu C H. Dynamics for a two-species competition-diffusion model with two free boundaries. Nonlinearity, 2015, 28: 1–27

    Article  MathSciNet  Google Scholar 

  10. Lewis M A, Schmitz G. Biological invasion of an organism with separate mobile and stationary states: Modelling and analysis. Forma, 1996, 11: 1–25

    MathSciNet  MATH  Google Scholar 

  11. Li L, Sheng W J, Wang M X. Systems with nonlocal vs. local diffusions and free boundaries. J Math Anal Appl, 2020, 483: 123646

    Article  MathSciNet  Google Scholar 

  12. Liu S Y, Huang H M, Wang M X. A free boundary problem for a prey-predator model with degenerate diffusion and predator-stage structure. Discrete Contin Dyn Syst Ser B, 2020, 25: 1649–1670

    MathSciNet  MATH  Google Scholar 

  13. Liu S Y, Wang M X. Existence and uniqueness of solution of free boundary problem with partially degenerate diffusion. Nonlinear Anal Real World Appl, 2020, 54: 103097

    Article  MathSciNet  Google Scholar 

  14. Nowak M A, Bangham C R M. Population dynamics of immune responses to persistent viruses. Science, 1996, 272: 74–79

    Article  Google Scholar 

  15. Nowak M A, May R M. Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford: Oxford University Press, 2000

    MATH  Google Scholar 

  16. Perelson A S, Neumann A U, Markowitz M, et al. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science, 1996, 271: 1582–1586

    Article  Google Scholar 

  17. Stancevic O, Angstmann C N, Murray J M, et al. Turing patterns from dynamics of early HIV infection. Bull Math Biol, 2013, 75: 774–795

    Article  MathSciNet  Google Scholar 

  18. Wang J, Cao J F. The spreading frontiers in partially degenerate reaction-diffusion systems. Nonlinear Anal, 2015, 122: 215–238

    Article  MathSciNet  Google Scholar 

  19. Wang J P, Wang M X. The diffusive Beddington-DeAngelis predator-prey model with nonlinear prey-taxis and free boundary. Math Methods Appl Sci, 2018, 41: 6741–6762

    Article  MathSciNet  Google Scholar 

  20. Wang M X. On some free boundary problems of the prey-predator model. J Differential Equations, 2014, 256: 3365–3394

    Article  MathSciNet  Google Scholar 

  21. Wang M X. A diffusive logistic equation with a free boundary and sign-changing coefficent in time-periodic environment. J Funct Anal, 2016, 270: 483–508

    Article  MathSciNet  Google Scholar 

  22. Wang M X. Existence and uniqueness of solutions of free boundary problems in heterogeneous environments. Discrete Contin Dyn Syst Ser B, 2019, 24: 415–421

    MathSciNet  MATH  Google Scholar 

  23. Wang M X, Zhang Q Y. Dynamics for the diffusive Leslie-Gower model with double free boundaries. Discrete Contin Dyn Syst, 2018, 38: 2591–2607

    Article  MathSciNet  Google Scholar 

  24. Wang M X, Zhang Y. Two kinds of free boundary problems for the diffusive prey-predator model. Nonlinear Anal Real World Appl, 2015, 24: 73–82

    Article  MathSciNet  Google Scholar 

  25. Wang M X, Zhang Y. The time-periodic diffusive competition models with a free boundary and sign-changing growth rates. Z Angew Math Phys, 2016, 67: 132

    Article  MathSciNet  Google Scholar 

  26. Wang M X, Zhang Y. Note on a two-species competition-diffusion model with two free boundaries. Nonlinear Anal, 2017, 159: 458–467

    Article  MathSciNet  Google Scholar 

  27. Wang M X, Zhang Y. Dynamics for a diffusive prey-predator model with different free boundaries. J Differential Equations, 2018, 264: 3527–3558

    Article  MathSciNet  Google Scholar 

  28. Wang M X, Zhao J F. Free boundary problems for a Lotka-Volterra competition system. J Dynam Differential Equations, 2014, 26: 655–672

    Article  MathSciNet  Google Scholar 

  29. Wang M X, Zhao J F. A free boundary problem for the predator-prey model with double free boundaries. J Dynam Differential Equations, 2017, 29: 957–979

    Article  MathSciNet  Google Scholar 

  30. Wang M X, Zhao Y G. Free boundary problems for the diffusive competition system in higher dimension with sign-changing coefficients. IMA J Appl Math, 2016, 81: 255–280

    Article  MathSciNet  Google Scholar 

  31. Wang W D, Zhao X Q. Basic reproduction numbers for reaction-diffusion epidemic models. SIAM J Appl Dyn Syst, 2012, 11: 1652–1673

    Article  MathSciNet  Google Scholar 

  32. Wei X P, Ghosh S K, Taylor M E, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature, 1995, 373: 117–122

    Article  Google Scholar 

  33. Zhang Q Y, Wang M X. Dynamics for the diffusive mutualist model with advection and different free boundaries. J Math Anal Appl, 2019, 474: 1512–1535

    Article  MathSciNet  Google Scholar 

  34. Zhao J F, Wang M X. A free boundary problem of a predator-prey model with higher dimension and heterogeneous environment. Nonlinear Anal Real World Appl, 2014, 16: 250–263

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant Nos. 11771110 and 11971128). The authors thank the reviewers for their helpful comments and suggestions that significantly improve the initial version of this paper.

Author information

Authors and Affiliations

  1. School of Mathematics, Harbin Institute of Technology, Harbin, 150001, China

    Lei Li & Mingxin Wang

  2. School of Science and Engineering, The Chinese University of Hong Kong, Shenzhen, Shenzhen, 518172, China

    Siyu Liu

  3. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China

    Siyu Liu

Authors
  1. Lei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Siyu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mingxin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mingxin Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Liu, S. & Wang, M. A viral propagation model with a nonlinear infection rate and free boundaries. Sci. China Math. 64, 1971–1992 (2021). https://doi.org/10.1007/s11425-020-1680-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-020-1680-0

Keywords

MSC(2010)

Search

Navigation