Abstract
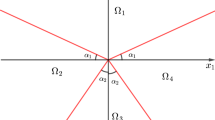
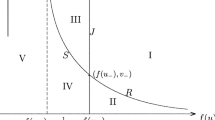
This article is a survey on the progress in the study of the generalized Riemann problems for MD Euler system. A new result on generalized Riemann problems for Euler systems containing all three main nonlinear waves (shock, rarefaction wave and contact discontinuity) is also introduced.
Similar content being viewed by others
References
Alinhac S. Existence d’ondes de rarefaction pour des systèmes quasi-linéaires hyperboliques multidimensionnels. Comm Partial Differential Equations, 1989, 14: 173–230
Artola M, Majda A. Nonlinear development of instabilities in supersonic vortex sheets I: The basic kink modes. Phys D, 1987, 28: 253–281
Artola M, Majda A. Nonlinear development of instabilities in supersonic vortex sheets II: Resonant interaction among kink modes. SIAM J Appl Math, 1989, 49: 1310–1349
Bui A T, Li D. The double shock front solutions for hyperbolic conservation laws in multi-dimensional space. Trans Amer Math Soc, 1989, 316: 233–250
Chang T, Chen G, Yang S. On the 2-D Riemann problem for the compressible Euler equations, I: Interaction of shocks and rarefaction waves. Discrete Contin Dyn Syst, 1995, 1: 555–584
Chang T, Chen G, Yang S. On the 2-D Riemann problem for the compressible Euler equations, II: Interaction of contact discontinuities. Discrete Contin Dyn Syst, 2000, 6: 419–430
Chen S X. Initial boundary value problems for quasilinear symmetric hyperbolic systems with characteristic boundary. Front Math China, 2007, 2: 87–102
Chen S X. Study of multidimensional systems of conservation laws: Problems, difficulties and progress. In: Proceedings of the International Congress of Mathematicians, vol. 3. New Delhi: Hindustan Book Agency, 2010, 1884–1900
Chen S X. Mult-dimensional nonlinear systems of conservation laws (in Chinese). Sci Sin Math, 2013, 43: 317–332
Chen S X, Li D. Cauchy problem with general discontinuous initial data along a smooth curve for 2-D Euler system. J Differential Equations, 2015, 257: 1939–1988
Chen S X, Qu A F. Two-dimensional Riemann problems for Chaplygin gas. SIAM J Math Anal, 2012, 44: 2146–2178
Coulombel J-F, Secchi P. The stability of compressible vortex sheets in two-space dimension. Indiana Univ Math J, 2004, 53: 941–1012
Coulombel J-F, Secchi P. Nonlinear compressible vortex sheets in two space dimensions. Ann Sciéc Norm Supér, 2008, 41: 85–139
Coulombel J-F, Secchi P. Uniqueness of 2-D compressible vortex sheets. Comm Pure Appl Anal, 2009, 8: 1439–1450
Courant R, Friedrichs K O. Supersonic Flow and Shock Waves. New York: Springer-Verlag, 1949
Dafermos C. Hyperbolic Conservation Laws in Coninuum Physics. New York: Springer, 2010
Douglis A. Some existence theorems for hyperbolic systems of partial differential equations intwo independent variables. Comm Pure Appl Math, 1952, 5: 119–154
Francheteau J, Metivier G. Existence de chocs faibles pour des systèmes quasi-linéaires hyperboliques multidimensionnels. C R Math Acad Sci Ser I, October 1998, 327: 725–728
Friedrichs K O. Nonlinear hyperbolic differential equations for functions of two independent variables. Amer J Math, 1948, 70: 555–589
Friedrichs K O. Symmetric positive linear differential equations. Comm Pure Appl Math, 1958, 11: 333–418
Gu C H. Differentiable solutions of symmetric positive partial differential equations. Chin Math Acta, 1964, 5: 541–555
Gu C H, Lee D, Hou Z. The Cauchy problem of quasi-linear hyperbolic system with discontinuous initial values I. Acta Math Sinica, 1961, 11: 314–323
Gu C H, Lee D, Hou Z. The Cauchy problem of quasi-linear hyperbolic system with discontinuous initial values II. Acta Math Sinica, 1961, 11: 324–327
Gu C H, Lee D, Hou Z. The Cauchy problem of quasi-linear hyperbolic system with discontinuous initial values III. Acta Math Sinica, 1962, 12: 132–143
Hamilton R S. The inverse function theorem of Nash and Moser. Bull Amer Math Soc, 1982, 7: 65–222
Hormander L. On the Nash-Moser implicit function theorem. Ann Acad Sci Fenn Math, 1985, 10: 255–259
Klainerman S. Long-time behavior of solutions to nonlinear evolution equations. Arch Ration Mech Anal, 1982, 78: 73–98
Kreiss H-O. Initial boundary value problems for hyperbolic systems. Comm Pure Appl Math, 1970, 23: 277–298
Lax P D. Hyperbolic systems of conservation laws. Comm Pure Appl Math, 1957, 10: 537–566
Lax P D, Phillips R S. Local boundary conditions for dissipative symmetric linear differential operators. Comm Pure Appl Math, 1960, 13: 427–455
Lee D T, Yu W T. Some existence theorems for quasi-linear hyperbolic systems of partial differential equations in two independent variables, I: Typical boundary value problems. Sci Sinica, 1964, 13: 529–549
Lee D T, Yu W T. Some existence theorems for quasi-linear hyperbolic systems of partial differential equations in two independent variables, II: Typical boundary value problems of functional formal and typical free boundary problems. Sci Sinica, 1964, 13: 551–562
Lee D T, Yu W T. Some existence theorems for quasi-linear hyperbolic systems of partial differential equations in two independent variables, III: General boundary vaue problems and general free boundary problems. Sci Sinica, 1965, 14: 1065–1067
Lee D T, Yu W T. Boundary value problem for the first-order quasi-linear hyperbolic systems and their applications. J Differential Equations, 1981, 41: 1–26
Li D. Rarefaction and shock waves for multi-dimensional hyperbolic conservation laws. Comm Partial Differential Equations, 1991, 16: 425–450
Li D. Compatibility of jump Cauchy data for non-isentropic Euler equations. J Math Anal Appl, 2015, 425: 565–587
Li D. Initial-boundary value problem for non-isentropic Euler equations with incompatible data. Http://www.math. wvu.edu/~li/research/pub/33 ibvp-shock.pdf
Li J. On the two-dimensional gas expansion for compressible Euler equations. SIAM J Appl Math, 2001, 62: 831–852
Li J, Zheng Y. Interaction of rarefaction waves of the two-dimensional self-similar Euler equations. Arch Rat Mech Anal, 2009, 193: 523–657
Li T T, Yu W C. Boundary Value Problem for Quasi-Linear Hyperbolic Systems. Durham: Duke University Press, 1985
Majda A. The existence and stability of multi-dimensional shock front. Bull Amer Math Soc (NS), 1981, 4: 342–344
Majda A. The stability of multi-dimensional shock front. Mem Amer Math Soc, 1983, 275: 1–96
Majda A, Osher S. Initial-Boundary value problems for hyperbolic equations with uniformly characteristic boundary. Comm Pure Appl Math, 1975, 28: 607–675
Majda A, Thomann E. Multidimensional shock fronts for second order wave equations. Comm Partial Differential Equations, 1990, 15: 983–1028
Metivier G. Interaction de deux chocs pour un systeme de deux lois de conservation en dimension deux d’espace. Trans Amer Math Soc, 1986, 296: 431–479
Metivier G. Ondes soniques. J Math Pure Appl, 1991, 70: 197–268
Nirenberg L. Variational and topological methods in nonlinear problems. Bull Amer Math Soc (NS), 1981, 4: 267–302
Rauch J, Massey F. Differentiability of solutions to hyperbolic initial-boundary value problems. Trans Amer Math Soc, 1974, 189: 303–318
Smoller J. Shock Waves and Reaction-Diffusion Equations. NewYork: Springer-Verlag, 1983
Zhang T, Zheng Y. Conjecture on the structure of solutions of the Riemann problem for two-dimensional gas dynamics systems. SIAM J Math Anal, 1990, 21: 593–630
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant Nos. 11031001, 11101101 and 11421061).
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor LI TaTsien on the Occasion of His 80th Birthday
Rights and permissions
About this article
Cite this article
Chen, S., Li, D. Generalised Riemann problem for Euler system. Sci. China Math. 60, 581–592 (2017). https://doi.org/10.1007/s11425-016-0437-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11425-016-0437-x