Skip to main content
SpringerLink
Log in

An Extended Weibull Model with Variable Periodicity

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

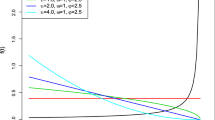
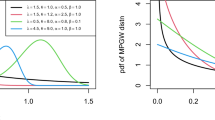
Abstract

A new distribution for the fluctuation of materials’ lifetime cumulative hazard rate is firstly proposed. The new distribution is extended from the Weibull distribution by adding a sine function. After that, the properties of its hazard rate function, cumulative hazard rate function, probability density function and cumulative distribution function are studied. The analysis result shows this distribution can well model the lifetime with variable and periodic hazard rate. Finally, the new distribution is verified with two real data sets as examples to demonstrate its capability.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zhao Y Y, Ma E, and Xu J, Reliability of compressive fracture strength of Mg-Zn-Ca bulk metallic glasses: Flaw sensitivity and Weibull statistics, Scripta Materialia, 2008, 58(6): 496–499.

    Article  Google Scholar 

  2. Zhao Y X and Liu H B, Weibull modeling of the probabilistic S-N curves for rolling contact fatigue, International Journal of Fatigue, 2014, 66: 47–54.

    Article  Google Scholar 

  3. Safari B, Modeling wind speed and wind power distributions in Rwanda, Renewable and Sustainable Energy Reviews, 2011, 15(2): 925–935.

    Article  MathSciNet  Google Scholar 

  4. Murthy D N P, Xie M, and Jiang R, Weibull Models, John Wiley & Sons, Inc., Hoboken, 2004.

    MATH  Google Scholar 

  5. Nadarajah S and Kotz S, On some recent modifications of Weibull distribution, IEEE Transactions on Reliability, 2005, 54(4): 561–562.

    Article  Google Scholar 

  6. Pham H and Lai C D, On recent generalizations of the Weibull distribution, IEEE Transactions on Reliability, 2007, 56(3): 454–458.

    Article  Google Scholar 

  7. Bebbington M, Lai C D, and Zitikis R, A flexible Weibull extension, Reliability Engineering and System Safety, 2007, 92: 719–726.

    Article  Google Scholar 

  8. Cordeiro G C, Ortega E M M, and Lemonte A J, The exponential-Weibull lifetime distribution, Journal of Statistical Computation and Simulation, 2014, 84(12): 2592–2606.

    Article  MathSciNet  Google Scholar 

  9. Almalki S J and Nadarajah S, A new discrete modified Weibull distribution, IEEE Transactions on Reliability, 2014, 63(1): 68–80.

    Article  Google Scholar 

  10. Rubio F J and Hong Y L, Survival and lifetime data analysis with a flexible class of distributions, Journal of Applied Statistics, 2016, 43(10): 1794–1813.

    Article  MathSciNet  Google Scholar 

  11. Singla N, Jain K, and Sharma S K, The Beta Generalized Weibull distribution: Properties and applications, Reliability Engineering and System Safety, 2012, 102: 5–15.

    Article  Google Scholar 

  12. Bagheri S F, Bahrami E B, and Ganjali M, The generalized modified Weibull power series distribution: theory and applications, Computational Statistics and Data Analysis, 2016, 94: 136–160.

    Article  MathSciNet  Google Scholar 

  13. Cordeiro G M, Ortega E M M, and Silva G O, The Kumaraswamy modified Weibull distribution: Theory and applications, Journal of Statistical Computation and Simulation, 2014, 84(7): 1387–1411.

    Article  MathSciNet  Google Scholar 

  14. He B, Cui W M, and Du X F, An additive modified Weibull distribution, Reliability Engineering and System Safety, 2016, 145: 28–37.

    Article  Google Scholar 

  15. Wong K L, The bathtub does not hold water any more, Quality and Reliability Engineering International, 1988, 4: 279–282.

    Article  Google Scholar 

  16. Wong K L, Roller-coaster curve in, Quality and Reliability Engineering International, 1989, 5(1): 29–36.

    Article  Google Scholar 

  17. Wong K L, Thysical basis for the roller-coaster hazard rate curve for electronics, Quality and Reliability Engineering International, 1991, 7(6): 489–495.

    Article  Google Scholar 

  18. Lai C D and Xie M, Stochastic Ageing and Dependence for Reliability, Springer Science+Business Media, Inc., New York, 2006.

    MATH  Google Scholar 

  19. Gurvich M R, Dibenedetto A T, and Rande S V, A new statistical distribution for characterizing the random length of brittle materials, Journal of Materials Science, 1997, 32: 2559–2564.

    Article  Google Scholar 

  20. Almalki S J and Yuan J S, A new modified Weibull distribution, Reliability Engineering and System Safety, 2013, 111: 164–170.

    Article  Google Scholar 

  21. Bourguignon M, Silva R P, and Cordeiro G M, The Weibull-G family of probability distributions, Journal of Data Science, 2014, 12: 53–68.

    MathSciNet  Google Scholar 

  22. Marshall A W and Olkin I, A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families, Biometrika, 1997, 84: 641–652.

    Article  MathSciNet  MATH  Google Scholar 

  23. Xie M, Tang Y, and Goh T N, A modified Weibull extension with bathtub-shaped failure rate function, Reliability Engineering and Systems Safety, 2000, 76: 279–285.

    Article  Google Scholar 

  24. Shafiei S, Darijani S, and Saboori H, Inverse Weibull power series distributions: Properties and applications, Journal of Statistical Computation and Simulation, 2016, 86(6): 1069–1094.

    Article  MathSciNet  Google Scholar 

  25. Nelson W, Applied Life Data Analysis, John Wiley & Sons, Inc, Hoboken, 1982.

    Book  MATH  Google Scholar 

  26. Hong Y, Meeker W Q, and Escobar L A, Avoiding problems with normal approximation confidence intervals for probabilities, Technometrics, 2008, 50(1): 64–68.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Science College, Inner Mongolia University of Technology, Hohhot, 010051, China

    Xiuyun Peng

Authors
  1. Xiuyun Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiuyun Peng.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant Nos. 11461051 and 11361036, and the Natural Science Foundation of Inner Mongolia under Grant No. 2014MS0112.

This paper was recommended for publication by Editor LI Qizhai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, X. An Extended Weibull Model with Variable Periodicity. J Syst Sci Complex 31, 841–858 (2018). https://doi.org/10.1007/s11424-018-7046-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-018-7046-7

Keywords

Search

Navigation