Skip to main content
SpringerLink
Log in

Reliability analysis of a cold standby repairable system with repairman extra work

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

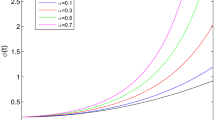
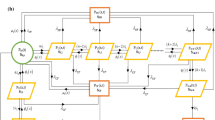
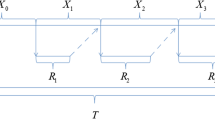
This paper deals with a cold standby repairable system with two identical units and one repairman who can do extra work in idle time. The authors are devoted to studying the unique existence and exponential stability of the system solution. C 0-semigroup theory is used to prove the existence of a unique nonnegative time-dependent solution of the system. Then by using the theory of resolvent positive operator, the authors derive that dynamic solution of the system exponentially converges to its steady-state one which is the eigenfunction corresponding to eigenvalue 0 of the system operator. Some reliability indices of the system are discussed with a different method from traditional one. The authors also make a profit analysis to determine the optimal service time outside the system to maximize the system profit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Papageorgiou E and Kokolakis G, Reliability analysis of a two-unit general parallel system with (n - 2) warm standbys, European Journal of Operational Research, 2002, 138: 127–141.

    Article  MathSciNet  Google Scholar 

  2. Zhang Y L and Wang G J, A geometric process repair model for a repairable cold standby system with priority in use and repair, Reliability Engineering and System Safety, 2009, 94: 1782–1787.

    Article  Google Scholar 

  3. Bieth B, Hong L, and Sarkar J, A standby system with two repair persons under arbitrary life-and repair times, Mathematical and Computer Modelling, 2010, 51: 756–767.

    Article  MathSciNet  MATH  Google Scholar 

  4. Gurov S V and Utkin L V, The time-dependent availability of repairable m-out-of-n and cold standby systems by arbitrary distributions and repair, Microelectronics and Reliability, 1995, 35(11): 1377–1393.

    Article  Google Scholar 

  5. Gurov S V and Utkin L V, Cold standby systems with inperfect and noninstantaneous switch-over mechanism, Microelectronics and Reliability, 1996, 36(10): 1425–1438.

    Article  Google Scholar 

  6. Gopalan M N and Kumar U D, On the transient behaviour of a repairable system with a warm standby, Microelectronics and Reliability, 1996, 36(4): 525–532.

    Article  Google Scholar 

  7. Kea J B, Lee W C, and Wang K H Reliability and sensitivity analysis of a system with multiple unreliable service stations and standby switching failures, Physica A, 2007, 380(4): 455–469.

    Article  Google Scholar 

  8. Zhang Y L, Yamb R C M, and Zuo M J, A bivariate optimal replacement policy for a multistate repairable system, Reliability Engineering and System Safety, 2007, 92: 535–542.

    Article  Google Scholar 

  9. Zhang Y L and Wang G J, A deteriorating cold standby repairable system with priority in use, European Journal of Operational Research, 2007, 183: 278–295.

    Article  MATH  Google Scholar 

  10. Jia J S and Wu S M, Optimizing replacement policy for a cold-standby system with waiting repair times, Applied Mathematics and Computation, 2009, 214: 133–141.

    Article  MathSciNet  MATH  Google Scholar 

  11. Wang W L and Xu G Q, The well-posedness and stability of a repairable standby human-machine system, Mathematical and Computer Modelling, 2006, 44: 1044–1052.

    Article  MathSciNet  MATH  Google Scholar 

  12. Wang W L and Xu G Q, Stability analysis of a complex standby system with constant waiting and different repairman criteria incorporating environmental failure, Applied Mathematical Modelling, 2009, 33: 724–743.

    Article  MathSciNet  MATH  Google Scholar 

  13. Shen Z F, Hu X X, and Fan W F, Exponential asymptotic property of a parallel repairable system with warm standby under common-cause failure, J. Math. Anal. Appl., 2008, 341: 457–466.

    Article  MathSciNet  MATH  Google Scholar 

  14. Tang Y H, On the transient departure process of M*/G/1 queueing system with single server vacation, Journal of Systems Science and Complexity, 2007, 20: 562–571.

    Article  MathSciNet  MATH  Google Scholar 

  15. Tang Y H, Yu M M, Yun X, and Huang S J, Reliability indices of discrete-time GeoX/G/1 queueing system with unreliable service station and multiple adaptive delayed vacations, Journal of Systems Science and Complexity, 2012, 25: 1122–1135.

    Article  MathSciNet  MATH  Google Scholar 

  16. Yue D Q and Zhang F, A discrete-time Geo/G/1 ketrial queue with J-vacation policy and general retrial times, Journal of Systems Science and Complexity, 2013, 26: 556–571.

    Article  MathSciNet  Google Scholar 

  17. Liu R B and Tang Y H, One-unit repairable system with multiple delay vacations, Chinese Journal of Engineering Mathematics, 2006, 23(4): 721–724.

    MathSciNet  MATH  Google Scholar 

  18. Rakhee J M and Singh M, Bilevel control of degraded machining system with warm standbys, setup and vacation, Applied Mathematical Modelling, 2004, 28: 1015–1026.

    Article  MATH  Google Scholar 

  19. Ke J C and Wang K H, Vacation policies for machine repair problem with two type spares, Applied Mathematical Modelling, 2007, 31: 880–894.

    Article  MATH  Google Scholar 

  20. Guo L L, Xu H B, Gao C, and Zhu G T, Stability analysis of a new kind n-unit series repairable system, Applied Mathematical Modelling, 2011, 35: 202–217.

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhang X, Reliability analysis of two supplemental equipments cold standby system of power station, Systems Engineering — Theory & Practice, 2013, 33(10): 2615–2622 (in Chinese).

    Google Scholar 

  22. Adams R, Sololev Spaces, Academic Press, New York, 1975.

    Google Scholar 

  23. Wolfgang A, Resolvent positive operators, Proc. Landon Math. Soc., 1987, 54: 321–349.

    MATH  Google Scholar 

  24. Cao J H and Cheng K, Introduction to Reliability Mathematics, Higher Education Press, Beijing, 1986.

    Google Scholar 

  25. Dunford N and Schwartz J T, Linear Operators, Part I, Wiley, New York, 1958.

    Google Scholar 

  26. Nagel R, One-parameter semigroup of positive operator, Lecture Notes in Mathematics, Springer-Verlag, New York, 1986.

    Book  Google Scholar 

  27. Taylor A E and Lay D C, Introduction to Functional Analysis, John Wiley & Sons, New York Chichester Bresbane Toronto, 1980.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Basic Courses, Beijing Union University, Beijing, 100101, China

    Xin Zhang

  2. Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Xin Zhang

Authors
  1. Xin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xin Zhang.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant No. 11201007.

This paper was recommended for publication by Editor WANG Shouyang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, X. Reliability analysis of a cold standby repairable system with repairman extra work. J Syst Sci Complex 28, 1015–1032 (2015). https://doi.org/10.1007/s11424-015-4081-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-015-4081-5

Keywords

Search

Navigation