Abstract
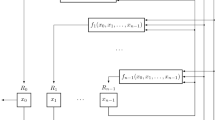
For nonlinear feedback shift registers (NFSRs), their greatest common subfamily may be not unique. Given two NFSRs, the authors only consider the case that their greatest common subfamily exists and is unique. If the greatest common subfamily is exactly the set of all sequences which can be generated by both of them, the authors can determine it by Gröbner basis theory. Otherwise, the authors can determine it under some conditions and partly solve the problem.
Similar content being viewed by others
References
Meier W and Staffelbach O, Fast correlation attacks on certain stream ciphers, Journal of Cryptology, 1989, 1(3): 159–176.
Canteaut A and Trabbia M, Improved fast correlation attacks using parity-check equations of weight 4 and 5, Advances in Cryptology-EUROCRYPT 2000 (ed. by Preneel B), Bruges, 2000.
Courtois N and Meier W, Algebraic attacks on stream ciphers with linear feedback, Advances in Cryptology-EUROCRYPT 2003 (ed. by Biham E), Warsaw, 2003.
Courtois N, Fast algebraic attacks on stream ciphers with linear feedback, Advances in Cryptology-CRYPTO 2003 (ed. by Boneh D), California, 2003.
Hell M, Johansson T, and Meier W, New Stream Cipher Designs: The Grain Family of Stream Ciphers, Springer-Verlag, Berlin, 2008.
Babbage S and Dodd M, New Stream Cipher Designs: The MICKEY Stream Ciphers, Springer-Verlag, Berlin, 2008.
Cannière C D and Preneel B, New Stream Cipher Designs: Trivium, Springer-Verlag Berlin, 2008.
Kjeldsen K, On the cycle of structure of a set of nonlinear shift registers with symmetric feedback functions, Journal of Combinatorial Theory Series A, 1976, 1(3): 154–169.
Hu H and Gong G, Periods on two kinds of nonlinear feedback shift registers with time varying feedback functions, International Journal of Foundations of Computer Science, 2011, 22(6): 1317–1329.
Annexstein F S, Generating De Bruijn sequences: An efficient implementation, IEEE Transactions on Computers, 1997, 46(2): 198–200.
Jansen C J, Investigations on nonlinear streamcipher systems: Construction and evaluation methods, Doctor’s degree thesis, Technical University of Delft, Netherlands, 1989.
Erdmann D and Murphy S, An approximate distribution for the maximum order complexity, Designs, Codes and Cryptography, 2005, 10(4): 1555–1563.
Dubrova E, A transformation from the Fibonacci to the Galois NLFSRs, IEEE Transactions on Information Theory, 2009, 55(11): 5263–5271.
Lidl R and Niederreiter H, Finite Fields, Cambridge University Press Oxford, 1997.
Cox D, Little J, and O’Shea D, Ideals, Varieties and Algorithms, Springer-Verlag, Berlin, 1996.
Gao X S and Huang Z, Characteristic set algorithms for equation solving in finite fields, Journal of Symbolic Computation, 2012, 47(6): 655–679.
Lang S, Algebra, Springer-Verlag Berlin, 2002.
Becker T and Weispfenning V, Gröbner Bases, a Computationnal Approach to Commutative Algebra, Springer-Verlag, Berlin, 1993.
Golomb S W, Shift Register Sequences, Aegean Park Press California, 1982.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the Natural Science Foundation of China under Grant Nos. 61272042, 61100202 and 61170235.
This paper was recommended for publication by Editor LI Ziming.
Rights and permissions
About this article
Cite this article
Wang, Z., Qi, W. & Tian, T. A note on determine the greatest common subfamily of two NFSRs by Gröbner basis. J Syst Sci Complex 28, 1231–1242 (2015). https://doi.org/10.1007/s11424-015-3072-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-015-3072-x