Abstract
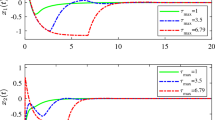
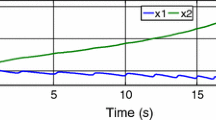
The dynamic linear state feedback control problem is addressed for a class of nonlinear systems subject to time-delay. First, using the dynamic change of coordinates, the problem of global state feedback stabilization is solved for a class of time-delay systems under a type of nonhomogeneous growth conditions. With the aid of an appropriate Lyapunov-Krasovskii functional and the adaptive strategy used in coordinates, the closed-loop system can be globally asymptotically stabilized by the dynamic linear state feedback controller. The growth condition in perturbations are more general than that in the existing results. The correctness of the theoretical results are illustrated with an academic simulation example.
Similar content being viewed by others
References
Qian C and Lin W, A continuous feedback approach to global strong stabilization of nonlinear systems, IEEE Transactions on Automatic Control, 2001, 46(7): 1061–1079.
Lin W and Qian C, Adaptive control of nonlinearly parameterized systems: A nonsmooth feedback framework, IEEE Transactions on Automatic Control, 2002, 47(5): 757–774.
Hua C, Liu P X, and Guan X, Backstepping control for nonlinear systems with time delays and applications to chemical reactor systems, IEEE Transactions on Industrial Electronics, 2009, 56(9): 3723–3732.
Polendo J and Qian C, A generalized homogeneous domination approach for global stabilization of inherently nonlinear systems via output feedback, International Journal of Robust and Nonlinear Control, 2007, 17(7): 605–629.
Qian C, A homogeneous domination approach for global output feedback stabilization of a class of nonlinear systems, Proceeding 2005 American Control Conference, Portland, U.S.A, 2005.
Qian C, Semi-global stabilization of a class of uncertain nonlinear systems by linear output feedback, IEEE Transactions on Circuit and Systems II, 2005, 52(4): 218–222.
Ding S and Li S, Global uniform asymptotical stability of a class of nonlinear cascaded system, International Journal of System Science, 2010, 41(11): 1310–1312.
Andrieu V, Praly L, and Astofi A, Homogeneous approximation and recursive observer design and output feedback, SIAM Journal on Control and Optimization, 2008, 47(4): 1814–1850.
Lei H and Lin W, Robust control of uncertain systems with polynomial nonlinearity by output feedback, International Journal of Robust and Nonlinear Control, 2009, 19(6): 692–723.
Li J, Qian C, and Frye M, A dual observer design for global output feedback stabilization of nonlinear systems with low-order and high-order nonlinearities, International Journal of Robust and Nonlinear Control, 2009, 19(15): 1697–1720.
Lei H and Lin W, Universal output feedback control of nonlinear systems with unknown growth rate, Proceedings of the 16th IFAC World Congress, Czech Republic, 2005.
Lei H and Lin W, A universal control approach for a family of uncertain nonlinear systems, Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference, Seville, Spain, 2005.
Sun Z and Liu Y, State-feedback stabilization control design for a class of time-delay high-order nonlinear systems, Proceedings of the 30th Chinese Control Conference, Yantai, China, 2011.
Chai L and Qian C, Global output feedback stabilization for a class of nonlinear time-delay systems, Under Minor Revisions of Transactions of the Institute of Measurement and Control, 2013: TIMC-12-0121.
Zhang X, Boukas E, and Baron L, Stabilizing controllers design for feedfoward nonlinear timedelay systems, Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 2009.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research is supported by US National Science Foundation under Grant No. HRD-0932339, the National Natural Science Foundation of China under Grant Nos. 61374038, 61374050, 61273119, 61174076, the Natural Science Foundation of Jiangsu Province of China under Grant No. BK2011253, and Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20110092110021.
This paper was recommended for publication by Editor HONG Yiguang.
Rights and permissions
About this article
Cite this article
Chai, L., Qian, C. State feedback stabilization for a class of nonlinear time-delay systems via dynamic linear controllers. J Syst Sci Complex 27, 453–462 (2014). https://doi.org/10.1007/s11424-014-3007-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-014-3007-y