Skip to main content
SpringerLink
Log in

Finite-time tracking control for motor servo systems with unknown dead-zones

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

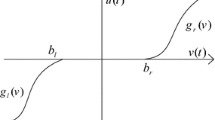
A finite-time tracking control scheme is proposed in this paper based on the terminal sliding mode principle for motor servo systems with unknown nonlinear dead-zone inputs. By using the differential mean value theorem, the dead-zone is represented as a time-varying system and thus the inverse compensation approach is avoided. Then, an indirect terminal sliding mode control (ITSMC) is developed to guarantee the finite-time convergence of the tracking error and to overcome the singularity problem in the traditional terminal sliding mode control. In the proposed controller design, the unknown nonlinearity of the system is approximated by a simple sigmoid neural network, and the approximation error is diminished by employing a robust term. Comparative experiments on a turntable servo system are conducted to show the superior performance of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Naso D, Cupertino F, and Turchiano B, Precise position control of tubular linear motors with neural networks and composite learning, Control Engineering Practice, 2010, 18(5): 515–522.

    Article  Google Scholar 

  2. Tao G and Kokotovic P V, Adaptive control of plants with unknown deadzones, IEEE Transactions on Automatic Control, 1994, 39(1): 59–68.

    Article  MathSciNet  MATH  Google Scholar 

  3. Wang X S, Su C Y, and Hong H, Robust adaptive control of a class of linear systems with unknown dead-zone, Automatica, 2004, 40(3): 407–413.

    Article  MathSciNet  MATH  Google Scholar 

  4. Hua C C, Wang Q G, and Guan X P, Adaptive tracking controller design of nonlinear systems with time delays and unknown dead-zone input, IEEE Transactions on Automatic Control, 2008, 53(7): 1753–1759.

    Article  MathSciNet  Google Scholar 

  5. Ibrir S, Xie W F, and Su C Y, Adaptive tracking of nonlinear systems with non-symmetric deadzone input, Automatica, 2007, 43(3): 522–530.

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang T P and Ge S S, Adaptive neural network tracking control of MIMO nonlinear systems with unknown dead zones and control directions, IEEE Transactions on Neural Network, 2009, 20(3): 483–497.

    Article  MathSciNet  Google Scholar 

  7. Na J, Ren X M, Herrmann G, and Qiao Z, Adaptive neural dynamic surface control for servo systems with unknown dead-zone, Control Engineering Practice, 2011, 19(11): 1328–1343.

    Article  Google Scholar 

  8. Imura J, Sugie T, and Yoshikawa T, Adaptive robust control of robot manipulators — Theory and experiment, IEEE Transactions on Robotics and Automation, 1994, 10(5): 705–710.

    Article  MathSciNet  Google Scholar 

  9. Xu L and Yao B, Adaptive robust precision motion control of linear motors with negligible electrical dynamics: Theory and experiments, IEEE Transactions on Mechatronics, 2001, 6(4): 444–452.

    Article  Google Scholar 

  10. Man Z H and Yu X H, Adaptive terminal sliding mode tracking control for rigid robotic manipulators with uncertain dynamics, JSME International Journal of Mechanical Systems, Machine Elements, and Manufacturing, 1997, 40(3): 493–502.

    Article  Google Scholar 

  11. Feng Y, Yu X H, and Man Z H, Non-singular terminal slidng mode control of rigid manipulators, Automatica, 2002, 38(12): 2159–2167.

    Article  MathSciNet  MATH  Google Scholar 

  12. Yu S, Yu X H, and Shirinzadehc B, Continuous finite-time control for robotic manipulators with terminal sliding mode, Automatica, 2005, 41(11): 1957–1964.

    Article  MathSciNet  MATH  Google Scholar 

  13. Liu Y L, Ji Y F, Cheng Z, and Jia T, Speed and rotor position identification for PMSM based on improved nonsingular terminal sliding-mode, Advanced Materials Research, 2012, 424–425: 796–800.

    Google Scholar 

  14. Zheng X M, Li Q M, Wang W, and Feng Y, Higher-order nonsingular terminal sliding mode deadtime compensation method in PMSM, 37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, November 2011, 592–597.

    Google Scholar 

  15. Li S H, Zhou M M, and Yu X H, Design and implementation of terminal sliding mode control method for PMSM speed regulation system, IEEE Transactions on Industrial Informatics, 10.1109/TII.2012.2226896, published online, November 2012.

    Google Scholar 

  16. Li S H, Liu H X, and Ding S H, A speed control for A PMSM using finite-time feedback control and disturbance compensation, Transactions of the Institute of Measurement and Control, 2010, 32(2): 170–187.

    Article  Google Scholar 

  17. Wang L Y, Chai T Y, and Zhai L F, Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics, IEEE Transactions on Industrial Electronics, 2009, 56(9): 3296–3304.

    Article  Google Scholar 

  18. Zhao D Y, Li S Y, and Gao F, A new terminal sliding mode control for robotic manipulators, International Journal of Control, 2009, 82(10): 1804–1813.

    Article  MathSciNet  MATH  Google Scholar 

  19. Na J, Ren X M, and Gao Y, et al. Adaptive neural network state predictor and tracking control for nonlinear time-delay systems, International Journal of Innovative Computing, Information, and Control, 2010, 6(2): 627–639.

    Google Scholar 

  20. Ren X M and Rad A B, Identification of nonlinear systems with unknown time delay based on time-delay neural networks, IEEE Transactions on Neural Networks, 2007, 18(5): 1536–1541.

    Article  Google Scholar 

  21. Ren X M, Lewis F L, and Zhang J L, Neural network compensation control for mechanical systems with disturbances, Automatica, 2009, 45(5): 1221–1226.

    Article  MathSciNet  MATH  Google Scholar 

  22. Na J, Ren X M, Shang C, and Guo Y, Adaptive neural network predictive control for nonlinear pure feedback systems with input delay, Journal of Press Control, 2012, 22(1): 194–206.

    Article  Google Scholar 

  23. Zou A M, Kumar K D, Hou Z G, and Liu X, Finite-time attitude tracking control for spacecraft using terminal sliding mode and chebyshev neural network, IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2011, 41(4): 950–963.

    Article  Google Scholar 

  24. Chen Q, Ren X M, and Oliver J A, Identifier-based adaptive neural dynamic surface control for uncertain DC-DC buck converter system with input constraint, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(4): 1871–1883.

    Article  MathSciNet  MATH  Google Scholar 

  25. Hong Y, Huang J, and Xu Y, On an output finite-time stabilization problem, IEEE Transactions on Automatic Control, 2001, 46(2): 305–309.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310023, China

    Qiang Chen, Li Yu & Yurong Nan

Authors
  1. Qiang Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yurong Nan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiang Chen.

Additional information

This research is supported by the Scientific Research Foundation of the Education Department of Zhejiang Province, China under Grant No. Y201329260, the Natural Science Foundation of Zhejiang Province, China under Grant No. LZ12E07003, and the National Natural Science Foundation of China under Grant No. 51207139.

This paper was recommended for publication by Editor HONG Yiguang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, Q., Yu, L. & Nan, Y. Finite-time tracking control for motor servo systems with unknown dead-zones. J Syst Sci Complex 26, 940–956 (2013). https://doi.org/10.1007/s11424-013-2153-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-013-2153-y

Key words

Search

Navigation