Denoising and Harmonic Detection Using Nonorthogonal Wavelet Packets in Industrial Applications

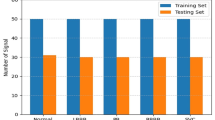
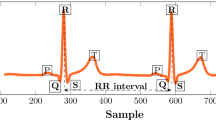
Abstract

New industrial applications call for new methods and new ideas in signal analysis. Wavelet packets are new tools in industrial applications and they have just recently appeared in projects and patents. In training neural networks, for the sake of dimensionality and of ratio of time, compact information is needed. This paper deals with simultaneous noise suppression and signal compression of quasi-harmonic signals. A quasi-harmonic signal is a signal with one dominant harmonic and some more sub harmonics in superposition. Such signals often occur in rail vehicle systems, in which noisy signals are present. Typically, they are signals which come from rail overhead power lines and are generated by intermodulation phenomena and radio interferences. An important task is to monitor and recognize them. This paper proposes an algorithm to differentiate discrete signals from their noisy observations using a library of nonorthonormal bases. The algorithm combines the shrinkage technique and techniques in regression analysis using Shannon Entropy function and Cross Entropy function to select the best discernable bases. Cosine and sine wavelet bases in wavelet packets are used. The algorithm is totally general and can be used in many industrial applications. The effectiveness of the proposed method consists of using as few as possible samples of the measured signal and in the meantime highlighting the difference between the noise and the desired signal. The problem is a difficult one, but well posed. In fact, compression reduces the level of the measured noise and undesired signals but introduces the well known compression noise. The goal is to extract a coherent signal from the measured signal which will be “well represented” by suitable waveforms and a noisy signal or incoherent signal which cannot be “compressed well” by the waveforms. Recursive residual iterations with cosine and sine bases allow the extraction of elements of the required signal and the noise. The algorithm that has been developed is utilized as a filter to extract features for training neural networks. It is currently integrated in the inferential modelling platform of the unit for Advanced Control and Simulation Solutions within ABB’s industry division. An application using real measured data from an electrical railway line is presented to illustrate and analyze the effectiveness of the proposed method. Another industrial application in fault detection, in which coherent and incoherent signals are univocally visible, is also shown.