Abstract
Conceptual constructive models are a type of scientific model that can be used to construct or reshape the target phenomenon conceptually. Though it has received scant attention from the philosophers, it raises an intriguing issue of how a conceptual constructive model can construct the target phenomenon in a conceptual way. Proponents of the conception of conceptual constructive models are not being explicit about the application of the constructive force of a model in the target construction. It is far from clear that how a conceptual constructive model exerts its constructive force on the constructed phenomenon of interest. Consequently, the function and the epistemic status of a conceptual constructive model are dubious at best. Making use of the conception of abstraction-as-aggregation, I argue that a conceptual constructive model can be used to construct the phenomenon of interest conceptually via a two-step process of abstraction: (1) abstracting away the lower-level details; and (2) aggregating the relevant information into a higher-level composite element. I contend that this process of abstraction, which is not playing the representational role as in a typical representational model, confers the constructive force on a model.
Similar content being viewed by others
Notes
The constructive force is the capability of a conceptual constructive model to alter or construct the target phenomenon in a conceptual way, subject to the way the model is used by the modeler. It is right to say that a model is agent-dependent to a certain extent, as it has been shown in my case study in Section 4 that the molecular docking algorithms and de novo protein design algorithms in a computational model are designed and implemented by scientists. As argued by Giere (2012) and Leonelli (2008), the relationship between a model and its target is the result of the intentional selection of the modeler.
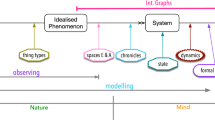
Knuuttila and Boon argue against the traditional representationalist view of models, according to which models are taken to be a ready-made tool, standing in an invariant representational relationship with the target. They maintain that it is problematic to “ground knowledge claims on some privileged representational relationship between a model and some real target system that prevails independently of our cognitive activities and abilities.” (2011, p. 317; My emphasis). They hold that the representationalist view has its limitation in accounting for the “epistemic value of model construction” (p. 310; Original emphasis) in the actual scientific practice.
According to Knuuttila and Boon, what is problematic with the prevailing representationalist view of models is that “the representational approach to models does not succeed in delivering what it is commonly taken to establish, i.e. to explain in virtue of what models give us knowledge.” (p. 331; Original emphasis)
Knuuttila and Boon conclude that the constructed scientifically accessible target phenomenon “already affords and limits the further modelling of the functioning of the heat engine and studying its theoretical limits.” (p. 321)
In their case study, Knuuttila and Boon discuss eight steps in the process of constructing the Carnot model. I shall not discuss all the steps here because they involve the co-construction of other epistemic resources such as concepts, principles, and theories. I shall only focus on their discussion on the construction of the target phenomenon.
I am friendly to Knuuttila and Boon’s claim that various epistemic resources such as concepts and epistemic aims jointly contribute to the construction of the scientifically accessible target phenomenon. What seems problematic to me is that they did not explain how these epistemic resources function to bring forth the constructive force. What they have demonstrated in their account is that the target phenomenon can be created by mere descriptions using concepts. It is far from clear that what type of description would lead to the eventual construction of target phenomenon.
In Knuuttila and Boon’s account, the constructive force of a model is derived from a description of the target phenomenon, as they write: “In fact, as we will show in the case of the Carnot model, modelling typically involves a theoretical (re)description of the target phenomenon […]” (p. 316; Original emphasis)
I do not deny the role played by abstractions in the construction of models.
Schelling’s famous checkerboard city model (Schelling 1978), according to which the dimes and pennies used to represent the economic agents possess only the preference for their neighbors while do not have any preference for life styles, serves as one of the examples. One may say that the dimes and pennies, which are the model elements, select autonomously their neighbors according to the rule stipulated in the model. The autonomy of dimes and pennies can be seen clearer when one is to consider the ‘coin-mover’ as a computer simulation software (which is also considered by Schelling) rather than a human—the coins are moved by rules stipulated in the model (in the form of algorithm), in an autonomous way even without the intervention of modelers. On a side note, it is worthwhile to point out that James Sakoda, who was a computational sociologist, has first devised the checkerboard models of discrimination (Sakoda 1971). Thanks to an anonymous referee who has brought my attention to Sakoda’s work.
The idea that abstraction is an autonomous process does not sound strange, I suppose, at least to those who accept the model-as-mediator view of scientific modeling (see Morgan and Morrison 1999). According to this view, models are characterized, in a general sense, as being autonomous from theories and experimental data. This autonomy of models is derived from the ways they are constructed—they are not derived entirely from theories or from data, but constituted by a motley of elements (Morrison and Morgan 1999, pp. 10–11). I argue in this paper that the autonomy of the process of abstraction-as-aggregation is the driving force that mobilizes the construction of the target phenomenon by a conceptual constructive model.
I thank an anonymous reviewer for bringing my attention to exploratory models.
Gelfert claims that “an analysis of [a model’s] exploratory uses is needed to account for situations where an underlying theory is unavailable” (Gelfert 2016, 75), and that “as in the case of experimentation, exploratory modeling is a distinct research activity only inasmuch as it takes place in the absence of a fully-formed theoretical framework.” (2016, 84).
For an overview of protein-protein interactions, see Karanicolas and Kuhlman (2009) for an excellent review.
The difference between composite model elements and auxiliary model elements is that the former is the essential ingredient which is indispensable in the construction of the target phenomenon (e.g. protein-protein interface in this case), whereas the latter does not have constructive force but merely play the supporting role in the construction of the target phenomenon. Examples of the supporting role include maintaining the homeostasis, hydrophobic effects, and so on. This supporting role of auxiliary model elements, viewed from the perspective of the epistemic studies of scientific modeling, constitutes the epistemic scaffolding in supporting the conceptual constructive force of the composite model elements.
I thank an anonymous referee for raising the point.
References
Boas, F. E., & Harbury, P. B. (2007). Potential energy functions for protein design. Current Opinion in Structural Biology., 17, 199–204.
Bokulich, A. (2011). How scientific models can explain. Synthese., 180, 33–45.
Bokulich, A. (2016). Fiction as a vehicle for truth: Moving beyond the ontic conception. The Monist., 99, 260–279.
Chakraborty, A., Mandloi, S., Lanczycki, C. J., Panchenko, A. R., & Chakrabarti, S. (2012). SPEER-SERVER: A web server for prediction of protein specificity determining sites. Nucleic Acids Research., 40, W242–W248.
Cheon, D.-J., & Orsulic, S. (2011). Mouse models of cancer. Annual Review of Pathology: Mechanisms of Disease., 6, 95–119.
Cunningham, A. D., Qvit, N., & Mochly-Rosen, D. (2017). Peptides and peptidomimetics as regulators of protein-protein interactions. Current Opinion in Structural Biology., 44, 59–66.
de Donato Rodríguez, X., & Zamora Bonilla, J. (2009). Credibility, idealisation, and model building: An inferential approach. Erkenntnis., 70, 101–118.
Dahiyat, B. I., Gordon, D. B., & Mayo, S. L. (1997). Automated design of the surface positions of protein helices. Protein Science., 6, 1333–1337.
Dahiyat, B. I., & Mayo, S. L. (1996). Protein design automation. Protein Science., 5, 895–903.
Der, B. S., Machius, M., Miley, M. J., Mills, J. L., Szyperski, T., & Kuhlman, B. (2012). Metal-mediated affinity and orientation specificity in a computationally designed protein homodimer. Journal of the American Chemical Society., 134(1), 375–385.
Fiorucci, S., & Zacharias, M. (2010). Prediction of protein-protein interaction sites using electrostatic desolvation profiles. Biophysical Journal, 98, 1921–1930.
Fromer, M., & Linial, M. (2010). Exposing the co-adaptive potential of protein-protein interfaces through computational sequence design. Bioinformatics., 26(18), 2266–2272.
Gelfert, A. (2016). How to do science with models: A philosophical primer. Springer.
Giere, R. (2012). Representing with physical models. In P. Humphreys & C. Imbert (Eds.), Models, simulations, and representations (pp. 209–215). New York: Routledge.
Goldstein, R. F. (1994). Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophysical Journal, 66(5), 1335–1340.
Gray, J. J. (2006). High-resolution protein-protein docking. Current Opinion in Structural Biology., 16, 183–193.
Green, S. (2013). When one model is not enough: Combining epistemic tools in systems biology. Studies in History and Philosophy of Biological and Biomedical Sciences., 44, 170–180.
Grosdidier, A., Zoete, V., & Michielin, O. (2011). SwissDock, a protein-small molecule docking web service based on EADock DSS. Nucleic Acids Research., 39, W270–W277.
Grüne-Yanoff, T. (2013). Appraising models nonrepresentationally. Philosophy of Science, 80, 850–861.
Havranek, J. J., & Harbury, P. B. (2003). Automated design of specificity in molecular recognition. Nature Structural Biology, 10(1), 45–52.
Hindriks, F. (2013). Explanation, understanding, and unrealistic models. Studies in History and Philosophy of Science., 44, 523–531.
Hochstein, E. (2016). One mechanism, many models: A distributed theory of mechanistic explanation. Synthese., 193, 1387–1407.
Huang, P.-S., Love, J. J., & Mayo, S. L. (2007). A de novo designed protein-protein interface. Protein Science., 16(12), 2770–2774.
Huang, P.-S., Boyken, S. E., & Baker, D. (2016). The coming of age of de novo protein design. Nature., 537, 320–327.
Humphreys, P. (2004). Extending ourselves: Computational science, empiricism, and scientific method. Oxford: Oxford University Press.
Ibarra, A., & Mormann, T. (2006). Scientific theories as intervening representations. Theoria., 55, 21–38.
Jones, S., & Thornton, J. M. (1996). Principles of protein-protein interactions. Proceedings of the National Academy of Sciences of the United States of America., 93(1), 13–20.
Kaplan, D. M., & Craver, C. F. (2011). The explanatory force of dynamical and mathematical models in neuroscience: A mechanistic perspective. Philosophy of Science, 78, 601–627.
Karanicolas, J., & Kuhlman, B. (2009). Computational design of affinity and specificity at protein-protein interfaces. Current Opinion in Structural Biology., 19, 458–463.
King, N. P., Sheffler, W., Sawaya, M. R., Vollmar, B. S., Sumida, J. P., André, I., Gonen, T., Yeates, T. O., & Baker, D. (2012). Computational design of self-assembling protein nanomaterials with atomic level accuracy. Science., 336(6085), 1171–1174.
Knuuttila, T., & Boon, M. (2011). How do models give us knowledge? The case of Carnot’s ideal heat engine. European Journal for Philosophy of Science., 1, 309–334.
Kortemme, T., Joachimiak, L. A., Bullock, A. N., Schuler, A. D., Stoddard, B. L., & Baker, D. (2004). Computational redesign of protein-protein interaction specificity. Nature Structural & Molecular Biology., 11(4), 371–379.
Kuorikoski, J., Lehtinen, A., & Marchionni, C. (2010). Economic modelling as robustness analysis. British Journal for the Philosophy of Science., 61(3), 541–567.
Leonelli, S. (2008). Performing abstraction: Two ways of modelling Arabidopsis thaliana. Biology and Philosophy, 23, 509–528.
Levy, A. (2011). Game theory, indirect modeling and the origin of morality. The Journal of Philosophy, 108(4), 171–187.
Levy, A. (2018). Idealization and abstraction: Refining the distinction. Synthese. https://doi.org/10.1007/s11229-018-1721-z.
Levy, A., & Bechtel, W. (2013). Abstraction and the organization of mechanisms. Philosophy of Science, 80, 241–261.
London, N., & Ambroggio, X. (2014). An accurate binding interaction model in de novo computational protein design of interactions: If you build it, they will bind. Journal of Structural Biology., 185(2), 136–146.
Love, A. C., & Travisano, M. (2013). Microbes modeling ontogeny. Biology and Philosophy, 28, 161–188.
Massimi, M. (2014). Natural kinds and naturalised Kantianism. Noȗs., 48(3), 416–449.
Massimi, M. (2015). ‘Working in a new world’: Kuhn, constructivism, and mind-dependence. Studies in History and Philosophy of Science., 50, 83–89.
Massimi, M. (2018). Perspectival modeling. Philosophy of Science, 85, 335–359.
Miłkowski, M. (2016). Explanatory completeness and idealization in large brain simulations: A mechanistic perspective. Synthese, 193, 1457–1478.
Morgan, M., & Morrison, M. (Eds.). (1999). Models as mediators: Perspectives on natural and social science. Cambridge: Cambridge University Press.
Morris, G.M. and Lim-Wilby, M. (2008). Molecular docking. In: A. Kukol (Ed.). Molecular Modeling of Proteins (pp. 365–382). Humana Press.
Morrison, M. (2015). Reconstructing reality: Models, mathematics, and simulations. Oxford: Oxford University Press.
Morrison, M., & Morgan, M. (1999). Models as mediating instruments. In M. Morgan & M. Morrison (Eds.), Models as mediators: Perspectives on natural and social science (pp. 10–37). Cambridge: Cambridge University Press.
Mou, Y., Huang, P. S., Hsu, F. C., Huang, S. J., & Mayo, S. L. (2015). Computational design and experimental verification of a symmetric protein homodimer. Proceedings of the National Academy of Sciences of the United States of America., 112(34), 10714–10719.
Noivirt-Brik, O., Horovitz, A., & Unger, R. (2009). Trade-off between positive and negative design of protein stability: From lattice models to real proteins. PLoS Computational Biology., 5(12), e1000592.
Ordorica, S. A. G. (2016). The explanatory role of abstraction processes in models: The case of aggregations. Studies in History and Philosophy of Science., 56, 161–167.
Peschard, I. (2011). Making sense of modeling: Beyond representation. European Journal for Philosophy of Science., 1, 335–352.
Portides, D. (2011). Seeking representations of phenomena: Phenomenological models. Studies in History and Philosophy of Science., 42, 334–341.
Rohwer, Y., & Rice, C. (2016). How are models and explanations related? Erkenntnis., 81, 1127–1148.
Rouse, J. (2009). Laboratory fictions. In M. Suárez (Ed.), Fictions in science: Philosophical essays on modeling and idealization (pp. 37–55). New York: Routledge.
Sakoda, J. A. (1971). The checkerboard model of social interaction. The Journal of Mathematical Sociology., 1(1), 119–132.
Schelling, T. C. (1978). Micromotives and macrobehavior. New York: Norton.
Sheinerman, F. B., Norel, R., & Honig, B. (2000). Electrostatic aspects of protein-protein interactions. Current Opinion in Structural Biology., 10(2), 153–159.
Stroganov, O. V., Novikov, F. N., Stroylov, V. S., Kulkov, V., & Chilov, G. G. (2008). Lead finder: An approach to improve accuracy of protein-ligand docking, binding energy estimation, and virtual screening. Journal of Chemical Information and Modeling., 48, 2371–2385.
Tee, S.-H. (2019). Abstraction as an autonomous process in scientific modeling. Philosophia., 48, 789–801. https://doi.org/10.1007/s11406-019-00092-6.
Thomson-Jones, M. (2010). Missing systems and the face value practice. Synthese., 172, 283-299.
Veit, W. (2020). Model pluralism. Philosophy of the Social Sciences, 50(2), 91–114.
Veit, W. (2019). Modeling morality. In Model-Based Reasoning in Science and, Modeling Morality. Technology, edited by Á. Nepomuceno-Fernández, L. Magnani, F. J. Salguero-Lamillar, C. Barés-Gómez, and M. Matthieu Fontaine, 83–102. Springer.
Weisberg, M. (2013). Simulation and similarity: Using models to understand the world. Oxford: Oxford University Press.
Wells, J. A., & McClendon, C. L. (2007). Reaching for high-hanging fruit in drug discovery at protein-protein interfaces. Nature., 450(7172), 1001–1009.
Wimsatt, W. C. (2002). Using false models to elaborate constraints on processes: Blending inheritance in organic and cultural evolution. Philosophy of Science, 69, S12–S24.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tee, SH. Conceptual Constructive Models and Abstraction-as-Aggregation. Philosophia 49, 819–837 (2021). https://doi.org/10.1007/s11406-020-00232-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11406-020-00232-3