Skip to main content
SpringerLink
Log in

A Dual Polarized Triple Band Stacked Elliptical Microstrip Patch Antenna for WLAN Applications

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

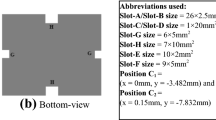
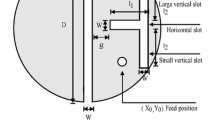
In this paper, a single coaxial feed dual polarized triple band stacked microstrip patch antenna for wireless applications is presented. The proposed stacked antenna has two resonating elements with lower layer consisting of a truncated corner square patch and upper layer with an elliptical patch. Both the layers of proposed antenna are printed on RT Duroid® 5880 substrate (having ϵr = 2.2). The antenna shows triple band resonance at 4.2, 4.8 and 5.8 GHz with circular polarization behaviour at the first two resonances and linear polarization characteristic in the third resonance respectively. The typical realized gain of proposed antenna is around 7 dB in all three resonating bands.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Shen, L. C. (1981). The elliptical microstrip antenna with circular polarization. IEEE Transactions on Antennas and Propagation, 29, 90–94.

    Article  Google Scholar 

  2. Kumprasert, N., & Kiranon, W. (1995). Simple and accurate formula for the resonant frequency of the circular microstrip disk antenna. IEEE Transactions on Antennas and Propagation, 43, 1331–1333.

    Article  Google Scholar 

  3. Long, S., & McAllister, M. (1982). The impedance of an elliptical printed-circuit antenna. IEEE Transactions on Antennas and Propagation, 30, 1197–1200.

    Article  Google Scholar 

  4. Abboud, F., Damiano, J. P., & Papiernik, A. (1990). A new model for calculating the input impedance of coax-fed circular microstrip antennas with and without air gaps. IEEE Transactions on Antennas and Propagation, 38, 1882–1885.

    Article  Google Scholar 

  5. Zhou, Y., Chen, C., Volakis, J.L. (2006). Proximity-coupled stacked patch antenna for tri-band GPS applications. In IEEE antennas and propagation society international symposium, pp. 2683–2686.

  6. Falade, O. P., Rehman, M. U., Gao, Y., Chen, X., & Parini, C. G. (2012). Single feed stacked patch circular polarized antenna for triple band GPS receivers. IEEE Transactions on Antennas and Propagation, 60, 4479–4484.

    Article  Google Scholar 

  7. Kumar, S., Kanaujia, B. K., Khandelwal, M. K., & Gautam, A. K. (2014). Stacked dual-band circularly polarized microstrip antenna with small frequency ratio. Microwave and Optical Technology Letters, 56, 1933–1937.

    Article  Google Scholar 

  8. Guha, D., & Siddiqui, J. Y. (2003). Resonant frequency of circular microstrip antenna covered with dielectric substrate. IEEE Transactions on Antennas and Propagation, 51, 1649–1652.

    Article  Google Scholar 

  9. James, J. R., & Hall, P. S. (1989). Handbook of microstrip antennas. London: Peter Peregrinus.

    Book  Google Scholar 

  10. Suzuki, Y., & Chiba, T. (1984). Computer analysis method for arbitrarily shaped microstrip antenna with multiterminals. IEEE Transactions on Antennas and Propagation, 32, 585–590.

    Article  Google Scholar 

  11. Bernhard, J. T., & Tousignant, C. J. (1999). Resonant frequencies of rectangular microstrip antennas with flush and spaced dielectric substrates. IEEE Transactions on Antennas and Propagation, 47, 302–308.

    Article  Google Scholar 

  12. Ansari, J. A., Singh, P., Dubey, S. K., Khan, R. U., & Vishvakarma, B. R. (2008). H-shaped stacked patch antenna for dual band operation. Progress in Electromagnetics Research, 5, 291–302.

    Article  Google Scholar 

  13. Gautam, A. K., Benjwal, P., & Kanaujia, B. K. (2012). A compact square microstrip antenna for circular polarization. Microwave and Optical Technology Letters, 54, 897–900.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronics and Communication Engineering, Ambedkar Institute of Advanced Communication Technologies and Research, Delhi, 110031, India

    Dinesh Kumar Raheja

  2. School of Computational and Integrative Sciences, Jawharlal Nehru University, New Delhi, 110067, India

    Binod Kumar Kanaujia

  3. Department of Electronics and Communication Engineering, SRM Institute of Science and Technology, Chennai, Tamil Nadu, 603203, India

    Sachin Kumar

Authors
  1. Dinesh Kumar Raheja
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Binod Kumar Kanaujia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sachin Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Binod Kumar Kanaujia.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raheja, D.K., Kanaujia, B.K. & Kumar, S. A Dual Polarized Triple Band Stacked Elliptical Microstrip Patch Antenna for WLAN Applications. Wireless Pers Commun 100, 1585–1599 (2018). https://doi.org/10.1007/s11277-018-5655-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-018-5655-z

Keywords

Search

Navigation