Secure communication in untrusted relay selection networks with wireless energy harvesting

Abstract

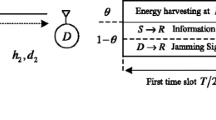
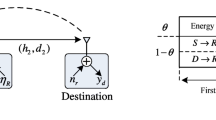
In this paper, we consider the secrecy performance of an energy-harvesting relaying system with Kth best partial relay selection where the communication of a multi-antenna source-destination pair is assisted via single-antenna untrusted relays. To protect confidential source messages from untrusted relays, transmit beamforming and destination jamming signals are used. The relays are energy-constrained nodes that use the power-splitting policy to harvest energy through the wireless signals from both the source and destination. For performance evaluation, closed-form expressions of the secrecy outage probability and average secrecy capacity (ASC) are derived for Nakagami-m fading channels. The analytical results are confirmed via Monte Carlo simulations. Numerical results provide valuable insights into the effect of various system parameters, such as relay location, number of relays, and power splitting ratio, on the secrecy performance. Specifically, the maximum ASC is achieved when the relay is located between the source and destination.

Appendices

Appendix 1

The secrecy outage probability in (15) can be rewritten as

$$\begin{aligned} P_{\text{out,low}} = 1 - \Pr \left({{\mathfrak{a}}X \varXi (Y;\gamma_{\text{th}}) {\gamma_{{\text{th}}}} - 1} \right) . \end{aligned}$$

(36)

Because $\varXi (Y;\gamma_{\text{th}}) \geqslant 0$ if and only if $y_1 \leqslant Y <\infty$, we can rewrite (36) as

$$\begin{aligned} P_{\text{out,low}} = 1 - \int \limits _{{y_1}}^\infty \left( {1 - {F_X}\left( \frac{\gamma_{\text {th}} - 1}{{\mathfrak{a}}\varXi (y;\gamma_{\text{th}})} \right) } \right) {f_Y}\left( y \right) dy. \end{aligned}$$

(37)

1.1 Calculation for $P_{\text{out,low}}^{\text{KBFC}}$

Substituting $F_X(x)$ and $f_Y(y)$ for the KBFC scheme in to (37), and using [14, Eq. (8.356.3)], $P_{\text{out,low}}^{\text{KBFC}}$ can be expressed as

$$\begin{aligned} P_{{\text {out,low}}}^{{\text {KBFC}}} =&1 + \sum \limits _{k = 0}^{K - 1} \sum \limits _{\begin{array}{c} n = 0 \\ k + n \ne 0 \end{array}} ^{L - k} \left( {\begin{array}{c}L\\ k\end{array}}\right) \left( {\begin{array}{c}L - k\\ n\end{array}}\right) \frac{{{{\left( { - 1} \right) }^n}m_2^{{N_2}{m_2}}}}{{\varGamma \left( {{N_2}{m_2}} \right) {\lambda _2 ^{{N_2}{m_2}}}}} \nonumber \\&\times \int \limits _{{y_1}}^\infty {{y^{{N_2}{m_2} - 1}}} {\left( {\frac{1}{{\varGamma \left( {{N_1}{m_1}} \right) }}\varGamma \left( {{N_1}{m_1},\frac{{{m_1}\left( {{\gamma _{{\text {th}}}} - 1} \right) }}{{{\lambda _1} {\mathfrak {a}} \varXi \left( {y;{\gamma _{{\text {th}}}}} \right) }}} \right) } \right) ^{k + n}}{e^{ - \frac{{{m_2}y}}{{{\lambda _2}}}}}dy. \end{aligned}$$

(38)

Expressing $\varGamma (\alpha ,x)$ as [14, Eq. (8.352.7)] and using the multinomial theorem [16, Eq. (26.4.9)] given by

$$\begin{aligned} {\left( {{x_1} + \ldots + {x_n}} \right) ^u} = \sum \limits _{{{\| {\mathbf{p}} \| }_1} = u} \left( {\begin{array}{c}u\\ {\mathbf{p}} \end{array}}\right) x_1^{{p_1}} \ldots x_n^{{p_n}}, \end{aligned}$$

(39)

$P_{\text{out,low}}^{\text{KBFC}}$ can be expressed as in (16).

1.2 Calculation for $P_{\text{out,low}}^{\text{KBSC}}$

Using $F_X(x)$ and $f_Y(y)$ for the KBSC scheme, the expression for $P_{\text{out,low}}^{\text{KBSC}}$ can be achieved using similar calculation steps for $P_{\text{out,low}}^{\text{KBFC}}$.

Appendix 2

Because the exact analysis for (19) appears to be difficult, the high-power SOP is approached using the asymptotic formulas of ${F_\mathcal {X}}\left( {x;m,\lambda } \right)$ and ${F_{{\mathcal {X}^{\left( K \right) }}}}\left( {x;m,\lambda } \right)$ as $x\rightarrow 0^+$. Using the series representation of the incomplete gamma function [14, Eq. (8.354.1)] and the fact that $\mathop {\lim }\limits _{x \rightarrow {0^ + }} \varGamma \left( {\alpha ,x} \right) = \varGamma \left( \alpha \right)$, we yield the following asymptotic formulas:

$$\begin{aligned} \mathop {\lim }\limits _{x \rightarrow {0^ + }} {F_\mathcal {X}}\left( {x;m,\lambda } \right)&= \frac{1}{{m!}}{\left( {\frac{x}{\lambda }} \right) ^m} \end{aligned}$$

(40)

$$\begin{aligned} \mathop {\lim }\limits _{x \rightarrow {0^ + }} {F_{{\mathcal {X}^{\left( K \right) }}}}\left( {x;m,\lambda } \right)&= \left( {\begin{array}{c}L\\ K - 1\end{array}}\right) {\left( {\frac{1}{{m!}}{{\left( {\frac{x}{\lambda }} \right) }^m}} \right) ^{L - K - 1}} \end{aligned}$$

(41)

2.1 Calculation for $P_{\text{out,HPL}}^{\text{KBFC}}$

Because $\underset{{\mathfrak {b}}\rightarrow \infty }{\lim } y_0 = \underset{({\mathfrak {a,b}})\rightarrow (\infty ,\infty )}{\lim } x_0=0$, $\mathcal {J}_1$ in (19) can be approximated using the asymptotic formula of $F_Y(y)$ for the KBFC scheme as follows.

$$\begin{aligned} \mathcal {J}_1&\approx \frac{1}{{\left( {{N_2}{m_2}} \right) !}}{\left( {\frac{{{m_2}{y_0}}}{{{\lambda _2}}}} \right) ^{{N_2}{m_2}}}. \end{aligned}$$

(42)

Using $f_Y(y)$ and the asymptotic formula of $F_X(x)$ for the KBFC scheme, $\mathcal {J}_2$ in (19) can be approximated by

$$\begin{aligned} \mathcal {J}_2&\approx \left( {\begin{array}{c}L\\ K - 1\end{array}}\right) \frac{(\mu _1y_0^2)^{{N_1}{m_1}\left( {L - K + 1} \right) }}{{\varGamma \left( {{N_2}{m_2}} \right) \varGamma {{\left( {{N_1}{m_1} + 1} \right) }^{L - K + 1}}}} \sum \limits _{n = 0}^{{N_1}{m_1}\left( {L - K + 1} \right) } \left( {\begin{array}{c}{N_1}{m_1}({L - K + 1} )\\ n\end{array}}\right) \nonumber \\&\quad \times {\left( {\frac{{{m_2}{\mathfrak {c}}}}{{{\lambda _2}}}} \right) ^n}\left( {{\mathbf {1}}\left( {n < {N_2}{m_2}} \right) {\mathcal {J}_{{\text {2,a}}}} + {\mathbf {1}}\left( {n \geqslant {N_2}{m_2}} \right) {\mathcal {J}_{{\text {2,a}}}}} \right) , \end{aligned}$$

(43)

where ${\mathcal {J}_{{\text {2,a}}}} = \int \limits _{{m_2}{y_0}/{\lambda _2}}^\infty {z_1^{{N_2}{m_2} - n - 1}} {e^{ - {z_1}}}d{z_1}$ and ${z_1} = \frac{{{m_2}y}}{{{\lambda _2}}}$. It can be seen that in the case of $n < {N_2}{m_2}$, we have

$$\begin{aligned} \mathop {\lim }\limits _{{y_0} \rightarrow {0^ + }} {\mathcal {J}_{{\text {2,a}}}} = \varGamma \left( {{N_2}{m_2} - n} \right) , \end{aligned}$$

(44)

and in the case of $n\geqslant N_2m_2$, $\mathcal {J}_{2,a}$ can be solved with help from [14, Eq. (3.351.4)] as follows.

$$\begin{aligned} {\mathcal {J}_{{\text {2,a}}}} =&\frac{{{{\left( { - 1} \right) }^{n - {N_2}{m_2} + 1}}}}{{\left( {n - {N_2}{m_2}} \right) !}}Ei\left( { - \frac{{{m_2}{y_0}}}{{{\lambda _2}}}} \right) + {e^{ - \frac{{{m_2}{y_0}}}{{{\lambda _2}}}}} \nonumber \\&\times \sum \limits _{u = 0}^{n - {N_2}{m_2} - 1} {\frac{{{{\left( { - 1} \right) }^u}\left( {n - {N_2}{m_2} - u - 1} \right) !}}{{\left( {n - {N_2}{m_2}} \right) !}}{{\left( {\frac{{{\lambda _2}}}{{{m_2}{y_0}}}} \right) }^{n - {N_2}{m_2} - u}}} . \end{aligned}$$

(45)

Using (42), (44) and (45), $P_{\text{out,HPL}}^{\text{KBFC}}$ can be expressed as in (20).

2.2 Calculation for $P_{\text{out,HPL}}^{\text{KBSC}}$

Using the asymptotic formula of $F_Y(x)$ and $F_X(x)$ for the KBSC scheme, and follows the same steps of 6.3.1, $P_{\text{out,HPL}}^{\text{KBSC}}$ can be expressed as in (21).

Appendix 3

According to [17], we can calculate ${\mathcal{C}}_{\text{erg,r}}$ as

$$\begin{aligned} {\mathcal {C}_{{\text {erg,r}}}} = \frac{1}{{\ln \left( 2 \right) }}\int \limits _0^{ + \infty } {\frac{{1 - {F_{{\gamma _{\text {r}}}}}\left( \gamma \right) }}{{1 + \gamma }}} d\gamma , \end{aligned}$$

(46)

where $F_{\gamma _r}(\gamma )$ is the CDF of $\gamma _r$. From (6), $F_{\gamma _r}(\gamma )$ can be calculated as

$$\begin{aligned} {F_{{\gamma _{\text {r}}}}}\left( \gamma \right) = \Pr \left( {\frac{{{\mathfrak {a}}X}}{{{\mathfrak {b}}Y + 1}} < \gamma } \right) = \int \limits _0^{ + \infty } {{F_X}} \left( {\frac{{\gamma \left( {{\mathfrak {b}}y + 1} \right) }}{{\mathfrak {a}}}} \right) {f_Y}\left( y \right) dy \end{aligned}$$

(47)

Because ${\mathcal{C}}_{\text{erg,d}}$ does not admit closed form expressions, ${\mathcal{C}}_{\text{erg,d}}$ can be evaluated by its lower bound obtaining by using Jensen’s inequality for a convex function $f(x)=\ln (1+e^{\ln (x)})$ as follows.

$$\begin{aligned} {\mathcal {C}_{{\text {erg,d,low}}}}\mathop = {\log _2}\left( {1 + {e^{\mathbb {E}\left\{ {\ln \left( {{\gamma _d}} \right) } \right\} }}} \right) , \end{aligned}$$

(48)

From (9a), (48) can be rewritten as

$$\begin{aligned} {\mathcal {C}_{{\text {erg,d,low}}}} = {\log _2}\left( {1 + {e^{\ln \left( {\mathfrak {a}} \right) + {\mathcal {J}_3} + {\mathcal {J}_4} - {\mathcal {J}_5}}}} \right) , \end{aligned}$$

(49)

where ${\mathcal {J}_3} = \mathbb {E}\left\{ {\ln \left( X \right) } \right\} ,{\mathcal {J}_4} = \mathbb {E}\left\{ {\ln \left( Y \right) } \right\}$ and ${\mathcal {J}_5} = \ln ( {\mathfrak {c}} ) + \mathbb {E}\left\{ {\ln \left( { \tfrac{Y}{{\mathfrak {c}}} + 1} \right) } \right\}$.

3.1 Calculation for $F_{{\gamma _r}}^{\text{KBFC }}\left( \gamma \right)$

Substituting ${F_X}\left( x \right)$ and ${f_Y}\left( y \right)$ for the KBFC scheme into (47), we have

$$\begin{aligned} {F_{{\gamma _{\text {r}}}}}\left( \gamma \right) = \int \limits _0^{ + \infty } {{F_{{\mathcal {X}^{\left( K \right) }}}}\left( {\frac{{\gamma \left( {{\mathfrak {b}}y + 1} \right) }}{{\mathfrak {a}}};{N_1}{m_1},\frac{{{\lambda _1}}}{{{m_1}}}} \right) } {f_\mathcal {X}}\left( {y;{N_2}{m_2},\frac{{{\lambda _2}}}{{{m_2}}}} \right) dy. \end{aligned}$$

(50)

Using (1), ( 12), (39) and [14, Eq. (3.351.3)], (50) can be rewritten as

$$\begin{aligned} F_{\gamma_{\text{r}}} (\gamma ) = \sum \limits _{k = 0}^{K - 1} {\sum \limits _{n = 0}^{L - k} {\sum \limits _{\left\| \mathbf{p ^{(1)}} \right\| _1 = k + n} {\sum \limits _{u = 0}^{{\omega _1}} {{\mathcal {I}_1}\left( {k,n,\mathbf{p ^{(1)}},u} \right) } } } } \frac{{{\gamma ^{{\omega _1}}}}}{{{{\left( {\gamma + {\mu _3}} \right) }^{{N_2}{m_2} + u}}}}{e^{ - \frac{{{m_1}\left( {k + n} \right) \gamma }}{{{{\mathfrak {a}}\lambda _1}}}}}. \end{aligned}$$

(51)

3.2 Calculation for $\mathcal {C}^\text{KBFC}_{\text{erg,r}}$

Substituting (51) into (46), ${\mathcal{C}}^{\text{KBFC}}_{\text{erg,r}}$ can be calculated as

$$\begin{aligned} \mathcal {C}_{{\text {erg,r}}}^{{\text {KBFC}}} = - \sum \limits _{k = 0}^{K - 1} \sum \limits _{\begin{array}{c} n = 0 \\ k + n \ne 0 \end{array}} ^{L - k} \sum \limits _{{{\left\| {\mathbf{p ^{(1)}}} \right\| }_1} = k + n} \sum \limits _{u = 0}^{{\omega _1}} \tfrac{{\mathcal {I}_1}\left( {k,n,\mathbf{p ^{(1)}},u} \right) }{\ln (2)} \int \limits _0^{ + \infty } {{\gamma ^{{\omega _1}}}{\mathcal {J}_6}\left( \gamma \right) } {e^{ - \frac{{{m_1}\left( {k + n} \right) \gamma }}{{{{\mathfrak {a}}\lambda _1}}}}}d\gamma , \end{aligned}$$

(52)

where ${\mathcal {J}_6}\left( \gamma \right) = {\left( {1 + \gamma } \right) ^{ - 1}}{\left( {\gamma + {\mu _3}} \right) ^{ - {N_2}{m_2} - u}}$.

Using the partial fraction expansion for ${\mathcal {J}_6}(\gamma )$, we have ${\mathcal {J}_6}\left( \gamma \right) = \frac{{{\mathcal {A}_0}}}{{\left( {\gamma + 1} \right) }} + \sum \limits _{j = 1}^{{N_2}{m_2} + u} {\frac{{{\mathcal {A}_j}}}{{{{\left( {\gamma + {\mu _3}} \right) }^j}}}}$; then, applying [14, Eq. (3.383.10) and Eq. (9.211.4)] on (52), $\mathcal {C}_{{\text {erg,r}}}^{{\text {KBFC}}}$ can be expressed as in (26).

3.3 Calculation for $\mathcal {C}^{\text{KBFC}}_{\text{erg,d}}$

Using $f_X(x)$ for the KBFC scheme, (39) and [14, Eq. (4.352.1)], $\mathcal {J}_3$ can be calculated as in (27).

Similarly, $\mathcal {J}_4$ for the KBFC scheme can be calculated as ${\mathcal{J}}_{\text{4,a}}$ given as (28).

Using $f_Y(y)$ for the KBFC scheme, ${\mathcal{J}}_{\text{5}}$ can be calculated as

$$\begin{aligned} {\mathcal {J}_{5,{\text {a}}}} = \ln ( {\mathfrak {c}} ) + \frac{1}{{\varGamma \left( {{N_2}{m_2}} \right) }}\int \limits _0^{ + \infty } {\ln \left( {\frac{{{\lambda _2}}}{{{{\mathfrak {c}}m_2}}}{z_2} + 1} \right) z_2^{{N_2}{m_2} - 1}} {e^{ - {z_2}}}d{z_2}. \end{aligned}$$

(53)

where $z_2=m_2y/{\lambda _2}$. With the help of [14, Eq. (4.337.5)], (53) can be rewritten as in (29).

Finally, $\mathcal {C}^{\text{KBFC}}_{\text{erg,d}}$ can be bounded below as

$$ {\mathcal{C}}_{{\text{erg,d,low}}}^{\text{KBFC}} = \log_{2}\left(1 + e^{\ln({\mathfrak{a}}) + {\mathcal{J}}_{\text{3,a}} + {\mathcal{J}}_{\text{4,a}} - {\mathcal{J}}_{\text{5,a}}} \right) , $$

(54)

To this end, substituting (26) and (54) into (24), we can obtain the desired result.