Abstract
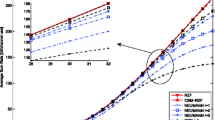
Several approximation approaches including the Gauss–Seidel (GS) method have been proposed to reduce the complexity of matrix inversion for zero-forcing pre-coding in massive multiple-input–multiple-output systems. However, extra computation is required to obtain the matrix inversion from the iteration result of the GS method. In this paper, we propose a new GS-based matrix inversion approximation (GSBMIA) approach. Unlike the traditional GS method, the GSBMIA approach approximates the matrix inversion, which will simplify further calculations. Furthermore, in order to speed up convergence, we propose a joint algorithm based on the GSBMIA and Newton iteration method where the GSBMIA approach is employed to provide an efficient searching direction for the following Newton iterations. Compared with other approximation methods, the joint algorithm can accommodate more single antenna users for the same base station antenna number. Simulation results demonstrate that the joint algorithm and the GSBMIA approach converge faster than the Neumann series and Newton iteration method.



Similar content being viewed by others
References
Andrews, J. G., Buzzi, S., Wan, C., Hanly, S. V., Lozano, A., Soong, A. C. K., et al. (2014). What will 5G be? IEEE Journal on Selected Areas in Communications, 32(6), 1065–1082.
Lu, L., Li, G. Y., Swindlehurst, A. L., Ashikhmin, A., & Zhang, R. (2014). An overview of massive MIMO: benefits and challenges. IEEE Journal of Selected Topics in Signal Processing, 8(5), 742–758.
Gao, X., Dai, L., Ma, Y., & Wang, Z. (2014). Low-complexity near-optimal signal detection for uplink large-scale MIMO systems. Electronics Letters, 50(18), 1326–1328.
Yin, B., Wu, M., Cavallaro, J. R., & Studer, C. (2014). Conjugate gradient-based soft-output detection and precoding in massive MIMO systems. In Global communications conference (GLOBECOM), 2014 IEEE, Austin, TX, 8–12 December 2014 (pp. 3696–3701).
Gao, X., Dai, L., Zhang, J., Han, S., & Chih-Lin, I. (2015). Capacity-approaching linear precoding with low-complexity for large-scale MIMO systems. In 2015 IEEE international conference on communications (ICC), London, 8–12 June 2015 (pp. 1577–1582).
Rosario, F., Monteiro, F. A., & Rodrigues, A. (2016). Fast matrix inversion updates for massive MIMO detection and precoding. IEEE Signal Processing Letters, 23(1), 75–79.
Wu, M., Yin, B., Wang, G., Dick, C., Cavallaro, J. R., & Studer, C. (2014). Large-scale MIMO detection for 3GPP LTE: algorithms and FPGA implementations. IEEE Journal of Selected Topics in Signal Processing, 8(5), 916–929.
Tang, C., Liu, C., Yuan, L., & Xing, Z. (2016). High precision low complexity matrix inversion based on Newton iteration for data detection in the massive MIMO. IEEE Communications Letters. doi:10.1109/LCOMM.2015.2514281.
Rusek, F., Persson, D., Lau, B. K., Larsson, E. G., Marzetta, T. L., Edfors, O., et al. (2013). Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Processing Magazine, 30(1), 40–60.
Zhu, D., Li, B., & Liang, P. (2015). On the matrix inversion approximation based on Neumann series in massive MIMO systems. In 2015 IEEE international conference on communications (ICC), 8–12 June 2015 (pp. 1763–1769).
Acknowledgments
This work is supported by “Beijing Key Laboratory of Work Safety Intelligent Monitoring (Beijing University of Posts and Telecommunications)”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Shao, L., Zu, Y. Approaches of approximating matrix inversion for zero-forcing pre-coding in downlink massive MIMO systems. Wireless Netw 24, 2699–2704 (2018). https://doi.org/10.1007/s11276-017-1496-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-017-1496-z