Abstract
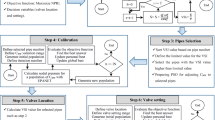
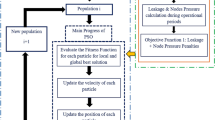
This paper investigates an effective and practical method to define optimal operational scheduling of available Partially Closed Valves (PCVs) for pressure management in Water Distribution Networks (WDNs). The aim is to determine which of the valves and how much does it is opened every hour of the day to maximize the Network Pressure Reliability Index (NPRI) of WDNs. The Particle Swarm Optimization (PSO) algorithm is applied to find which of valves needs adjustment by using the Pipe Closure Index (PCI) in a calibration process, and the Ant Colony Optimization (ACO) algorithm is used to find the setting of valves. The developed models are prepared by linking the optimization algorithm with the hydraulic simulator (EPANET) in the MATLAB. A sample network and real WDN are used to validate the proposed method. The comparison of the results for the real WDN indicates that by using the proposed method, the average reliability index increases up to 32.6%, and the average leakage rate decreases up to 31.7%. So the proposed method is effective in increasing the reliability and decreasing the leakage rate of the network.








Similar content being viewed by others
References
Ali M (2015) Knowledge-based optimization model for control valve locations in water distribution networks. Water Resour Plan Manag 141(1):1–7
Araujo LS, Ramos H, Coelho ST (2006) Pressure control for leakage minimisation in water distribution systems management. Water Resour Manag 20(1):133–149
Arulraj GP, Rao HS (1995) Concept of significance index for maintenance and design of pipe networks. Hydroinformatics 121(11):833–837
Avila FG, Anazco AA, Jara JO, Quezada CG, Delpino LF, Fernandez LR (2019) Pressure management for leakage reduction using pressure reducing valves. Case study in an Andean city. Alex Eng J 58(4):1313–1326
Bonvin G, Demassey S, Papeb C, Maïzia N, Mazauricb V, Samperio A (2017) A convex mathematical program for pump scheduling in a class of branched water networks. Appl Energy 185(2):1702–1711
Corcoran L, McNabola A, Coughlan P (2016) Optimization of water distribution networks for combined hydropower energy recovery and leakage reduction. Water Resour Plan Manag 142(2):1–8
Creaco E, Pezzinga G (2018) Comparison of algorithms for the optimal location of control valves for leakage reduction in WDNs. Water 10(4):1–13
Darvini G, Soldini L (2015) Pressure control for WDS management. A case study. Procedia Eng 119:984–993
De Marchis M, Freni G (2015) Pump as turbine implementation in a dynamic numerical model: cost analysis for energy recovery in water distribution network. Hydroinformatics 17(3):347–360
De Paola FD, Giugni M, Portlano D (2017) Pressure management through optimal location and setting of water distribution networks using a music-inspired approach. Water Resour Manag 31(5):1517–1533
Dini M, Asadi A (2019) Pressure management of large-scale water distribution network using optimal location and valve setting. Water Resour Manag 33(14):4701–4713
Dini M, Tabesh M (2014) A new method for simultaneous calibration of demand pattern and Hazen-Williams coefficients in water distribution systems. Water Resour Manag 28(7):2021–2034
Dini M, Tabesh M (2017a) Water distribution network quality model calibration; a case study: Ahar. Water Supply 16(5):1–13
Dini M, Tabesh M (2017b) A new reliability index for evaluating the performance of water distribution networks. J Water Wastew 29(3):1–16 (in Persian)
Dini M, Tanesh M (2019) Optimal renovation planning of water distribution networks considering hydraulic and quality reliability indices. Urban Water J 16(4):249–258
Do NC, Simpson AR, Deuerlein JW, Piller O (2018) locating inadvertently partially closed valves in water distribution systems. Water Resour Plan Manag 144(8):1–14
Dorigo M, Maniezzo V, Colorni A (1996) The ant system; Optimisation by a colony of cooperating agents. IEEE Transactions on Systems, Part B 26(1):29–41
Eberhart RC, Kennedy J (1995) A new optimizer using particle swarm theory. Proceedings of the sixth international symposium on micro machine and human science, IEEE, 4-6 Oct, Nagoya, Japan, pp 39-43
Gencoglu G, Merzib N (2017) Minimizing excess pressure by optimal valve location and opening determination in water distribution networks. Procedia Eng 186:319–326
Gungor M, Yarar U, Canturk U, Fırat M (2019) Increasing performance of water distribution network by using pressure management and database integration. Pipeline Syst Eng Pract 10(2):1–8
Gupta A, Kulat KD (2018) Leakage reduction in water distribution system using efficient pressure management techniques. Case study: Nagpur, India. Water Supply 18(6):2015–2027
Hashemi SS, Tabesh M, Ataeekia B (2013) Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J 11(5):1–13
Jowitt PW, Xu C (1990) Optimal valve control in water distribution networks. Water Resour Plan Manag 116(4):455–472
Khatavkar P, Mays LW (2019) Optimization-simulation model for real-time pump and valve operation of water distribution systems under critical conditions. Urban Water J 16(1):45–55
Lydon T, Coughlan P, McNabola A (2017) Pressure management and energy recovery in water distribution networks: development of design and selection methodologies using three pump-as-turbine case studies. Renew Energy 114:1038–1050
Nerantzis D, Pecci F, Stoianov I (2019) Optimal control of water distribution networks without storage. Eur J Oper Res 284(1):345–354
Page PR, Zulu S, Mothetha ML (2019) Remote real-time pressure control via a variable speed pump in a specific water distribution system. Water Supply 68(1):20–28
Patelisa M, Kanakoudis V, Gonelasa K (2016) Pressure management and energy recovery capabilities using PATs. Procedia Eng 162:503–510
Rossman LA (2000) EPANET 2 USERSMANUAL. U.S. Environmental Protection Agency, Washington, D.C., EPA/600/R-00/057
Samir N, Kanosh R, Elbarki W, Fleifle A (2017) Pressure control for minimizing leakage in water distribution systems. Alex Eng J 56:601–612
Venturini M, Alvisi S, Simani S, Manservigi L (2017) Energy production by means of pumps as turbines in water distribution networks. Energies 10(10):2–13
Wright R, Abraham E, Parpas P, Stoianov I (2015) Optimized control of pressure reducing valves in water distribution networks with dynamic topology. Procedia Eng 119:1003–1011
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this article.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Dini, M., Asadi, A. Optimal Operational Scheduling of Available Partially Closed Valves for Pressure Management in Water Distribution Networks. Water Resour Manage 34, 2571–2583 (2020). https://doi.org/10.1007/s11269-020-02579-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-020-02579-4