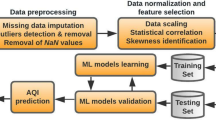
Abstract
Accurate rainfall prediction is a challenging task. It is especially challenging in Australia where the climate is highly variable. Australia’s climatic zones range from high rainfall tropical regions in the north to the driest desert region in the interior. The performance of prediction models may vary depending on climatic conditions. It is, therefore, important to assess and compare the performance of these models in different climatic zones. This paper examines the performance of data driven models such as the support vector machines for regression, the multiple linear regression, the k-nearest neighbors and the artificial neural networks for monthly rainfall prediction in Australia depending on climatic conditions. Rainfall data with five meteorological variables over the period of 1970–2014 from 24 geographically diverse weather stations are used for this purpose. The prediction performance of each model was evaluated by comparing observed and predicted rainfall using various measures for prediction accuracy.







Similar content being viewed by others
References
Australian weather and seasons (2013) http://www.australia.gov.au/about-australia/australian-story/austn-weather-and-the-seasons
Abbot J, Marohasy J (2012) Application of artificial neural networks to rainfall forecasting in Queensland, Australia. Adv Atmos Sci 29(4):717–730
Abbot J, Marohasy J (2014) Input selection and optimisation for monthly rainfall forecasting in Queensland, Australia, using artificial neural networks. Atmos Res 138:166–178
Aksoy H, Dahamsheh A (2009) Artificial neural network models for forecasting monthly precipitation in Jordan. Stochastic Environ Res Risk Assess 23:917–931
Al-Qahtani F, Crone S (2013) Multivariate k-nearest neighbour regression for time series data - A novel algorithm for forecasting UK electricity demand. In: The 2013 international joint conference on neural networks (IJCNN), pp 1–8
Awan J, Bae D (2014) Improving ANFIS based model for long-term dam inflow prediction by incorporating monthly rainfall forecasts. Water Resour Manag 28 (5):1185–1199
Chattopadhyay G, Chattopadhyay S, Jain R (2010) Multivariate forecast of winter monsoon rainfall in India using SST anomaly as a predictor: neurocomputing and statistical approaches. Compt Rendus Geosci 342(10):755–765
Chowdhury R, Beecham S (2013) Influence of SOI, DMI and Niño 3.4 on South Australian rainfall. Stoch Environ Res Risk Assess 27:1909–1920
Collobert R, Bengio S (2001) SVMTorch: Support vector machines for large-scale regression problems. J Mach Learn Res 1:143–160
Feng Q, Wen X, Li J (2015) Wavelet analysis-support vector machine coupled models for monthly rainfall forecasting in arid regions. Water Resour Manag 29(4):1049–1065
Garnaut R (2008) The Garnaut climate change review: final report. Cambridge University Press, Cambridge
Haykin S (2001) Neural networks: a comprehensive foundation. Upper Saddle River, N.J.: Prentice Hall
Karamouz M, Razavi S, Araghinejad S (2008) Long-lead seasonal rainfall forecasting using time-delay recurrent neural networks: a case study. Hydrol Process 22 (2):229–241
Kisi O, Cimen M (2012) Precipitation forecasting by using wavelet-support vector machine conjunction model. Eng Appl Artif Intell 25(4):783–792
Lin GF, Chen GR, Wu MC, Chou YC (2009) Effective forecasting of hourly typhoon rainfall using support vector machines. Water Resour Res 45(8):W08440. https://doi.org/10.1029/2009WR007911
Lorrai M, Sechi G (1995) Neural nets for modelling rainfall-runoff transformations. Water Resour Manag 9(4):299–313
Mekanik F, Imteaz M, Gato-Trinidad S, Elmahdi A (2013) Multiple regression and artificial neural network for long-term rainfall forecasting using large scale climate modes. J Hydrol 503:11–21
Mercer A, Dyer J, Zhang S (2013) Warm-season thermodynamically-driven rainfall prediction with support vector machines. Procedia Comput Sci 20:128–133
Meyer D, Dimitriadou E, Hornik K, Weingessel A, Leisch F (2015) e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. https://CRAN.R-project.org/package=e1071. R package version 1.6–7
Müller KR, Smola A, Rätsch G, Schölkopf B, Kohlmorgen J, Vapnik V (1997) Predicting time series with support vector machines. In: Gerstner W, Germond A, Hasler M, Nicoud JD (eds) Artificial neural networks – ICANN’97. ICANN 1997. Lecture notes in computer science, vol 1327. Springer, Berlin, Heidelberg, pp 999–1004
Nash J, Sutcliffe J (1970) River flow forecasting through conceptual models part I-A discussion of principles. J Hydrol 10(3):282–290
Nayak M, Ghosh S (2013) Prediction of extreme rainfall event using weather pattern recognition and support vector machine classifier. Theor Appl Climatol 114 (3-4):583–603
Omotosho J, Balogun A, Ogunjobi K (2000) Predicting monthly and seasonal rainfall, onset and cessation of the rainy season in West Africa using only surface data. Int J Climatol 20:865–880
R Core Team (2013) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/
Ramirez M, de Campos V, Haroldo F, Ferreira N (2005) Artificial neural network technique for rainfall forecasting applied to the Sao Paulo region. J Hydrol 301 (1):146–162
Schliep K, Hechenbichler K (2016) kknn: Weighted k-Nearest Neighbors. https://CRAN.R-project.org/package=kknn
Sharma V, van de Graaff S, Loechel B, Franks D (2013) Extractive resource development in a changing climate: learning the lessons from extreme weather events in Queensland. National Climate Change Adaptation Research Facility, Gold Coast, p 110
Shukla R, Tripathi K, Pandey A, Das I (2011) Prediction of Indian summer monsoon rainfall using Niño indices: a neural network approach. Atmos Res 102(1-2):99–109
Smola A, Schölkopf B (2004) A tutorial on support vector regression. Stat Comput 14:199–222
Venables W, Ripley B (2002) Modern applied statistics with S, 4th edn. Springer, New York. http://www.stats.ox.ac.uk/pub/MASS4
Wang E, Zhang Y, Luo J, Francis HS, Chiew F, Wang Q (2011) Monthly and seasonal streamflow forecasts using rainfall-runoff modeling and historical weather data. Water Resour Res 47:1–13
Yakowitz S, Karlsson M (1987) Nearest neighbor methods for time series, with application to rainfall/runoff prediction. In: Advances in the statistical sciences: stochastic hydrology. Springer, Berlin, pp 149–160
Acknowledgements
This research by Dr. A. Bagirov was supported by the Australian Research Counsil’s Discovery Projects funding scheme (Project No. DP140103213). The authors would like to thank the Editor and two anonymous referees for their comments that helped to significantly improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bagirov, A.M., Mahmood, A. A Comparative Assessment of Models to Predict Monthly Rainfall in Australia. Water Resour Manage 32, 1777–1794 (2018). https://doi.org/10.1007/s11269-018-1903-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-018-1903-y