Abstract
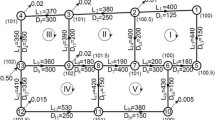
In this paper, a novel algorithm is proposed for balancing water looped network in steady state through a fully automated general framework of hydraulic networks regardless of their topological complexity. The model is developed by combining the following two steps, firstly a set of independent loops are identified based on a graph theoretical analysis in a looped network. Further the second step is devoted to the equilibrium process by determining the flow rate distribution within the network ducts and the pressure in the delivery nodes. The above such equilibrium process gives rise to a system of non linear algebraic equations which are solved numerically using both Hardy Cross (HC) and Newton Raphson (NR) methods. In HC method, the flow correction term is modified and a generalized expression is given to consider various possibilities of independent loops selection. Some real networks topologies that were commonly used as benchmarks, for testing various independent loops selection algorithms, are taken as case studies to apply the general automatic framework for hydraulic network analysis. Such network analysis enhances proving the applicability as well as the effectiveness of the proposed approach. Also, during the equilibrium procedure, it is proved that NR method is capable of producing accurate results and it converges more rapidly comparing to the widely used HC method. Moreover, it is demonstrated that NR’s iterative process, contrary to HC’s one, converges to reliable results even with a choice of random initial flow rates which makes a NR algorithm quite simple to implement without affecting the accuracy of the results.







Similar content being viewed by others
References
Alvarruiz F, Martínez-Alzamora F, Vidal AM (2015) Improving the Efficiency of the Loop Method for the Simulation of Water Distribution Systems. Journal of Water Resources Planning and Management. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000539
Alvisi S, Creaco E, Franchini M (2011) Segment identification in water distribution systems. UrbanWater Journal 8(4):203–217. https://doi.org/10.1080/1573062X.2011.595803
Ayad A, Awad H, Yassin A (2013) Developed hydraulic simulation model for water pipeline networks. Alex Eng J 52:43–49
Bellman R (1958) On a routing problem. Q Appl Math 16(1):87–90
Binder RC (1973) Fluid mechanics. Prentice-Hall, Inc, Englewood Cliffs
Bragalli C, D’Ambrosio C, Lee J, Lodi A, Toth P (2008) Water network design by MINLP. Rep. No. RC24495, IBM Research,Yorktown Heights
Brkić D (2011) Iterative methods for looped network pipeline calculation. Water Resour Manag 25:2951–2987. https://doi.org/10.1007/s11269-011-9784-3
Chandrashekar M, Stewart K (1975) Sparsity oriented analysis of large pipe networks. Journal of the Hydraulics Division 101(4):341–355
Creaco E, Franchini M (2014) Comparison of Newton-Raphson Global and Loop Algorithms for Water Distribution Network Resolution. Journal of Hydraulic Engineering 140(3):313–321. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000825
Creaco E, Franchini M (2015) The identification of loops in water distribution networks. 13th Computer Control for Water Industry Conference CCWI 2015 https://doi.org/10.1016/j.proeng.2015.08.878
Cross H (1936) Analysis of flow in network of conduits or conductors Bulletin No. 286, University of Illinois, Engineering Experimental Station, Urbana, II
Dijkstra EW (1959) A note on two problems in connexion with graphs. Numer Math 1:269–271
Divénot A (1980) A new mesh network calculation method. La Houille Blanche 6:365–375
Dobrnjac M (2012) Determination of Friction Coefficient in Transition Flow Region for Water Works and Pipelines Calculation. Annals of Faculty Engineering Hunedoara, International Journal of Engineering X(3):137–142
Fox RW, McDonald AT (1992) Introduction to fluid mechanics. Wiley, New York
Giles RV (1962) Theory and Problems of Fluid Mechanics and Hydraulics. Schaum Publishing Co. p274, New York
Haihong M, Mao B, Dezhang L, Jean-Claude R (1998) Study of flow and transport in fracture network using percolation theory. Appl Math Model 22:277–291
Kruskal JB (1956) On the shortest spanning subtree of a graph and the travelling salesman problem. Proc Am Math Soc 7:48–50
Lopes AMG (2003) Implementation of the hardy-cross method for the solution of piping networks. Wiley Periodicals Inc 117–125
Moosavian N, Jaefarzadeh MR (2014) Hydraulic Analysis of Water Supply Networks using Modified Hardy Cross Method. International Journal of Engineering Transactions C 27(9):1331–1338
Prim R (1957) Shortest connection networks and some generalizations. Bell Syst Tech J 36:1389–1401
Raad DN (2011) Multi-objective optimisation of water distribution systems design using metaheuristics. Dissertation, University of Stellenbosch
Sârbu I (1987) Computational model of hydraulic regime in complex water distribution networks. Hydrotechnics 8:309–314
Shamir U, Howard C (1968) Water distribution system analysis. J Hydraul Div 94:219–234
Shuang Q, Zhang M, Yuan Y (2014) Performance and reliability analysis of water distribution systems under cascading failures and the identification of crucial pipes. PLoS One 9(2):e88445. https://doi.org/10.1371/journal.pone.0088445
Spiliotis M, Tsakiris G (2011) Water distribution system analysis: Newton-Raphson method revisited. J Hydraul Eng 137:852–855
Todini E (2000) Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2:115–122
Todini E, Rossman, L (2013) Unified Framework for Deriving Simultaneous Equation Algorithms for Water Distribution Networks. Journal of Hydraulic Engineering 139(5):511–526. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000703
Travers K (1967) The mesh method in gas network analysis. Gas J 332:167–174
Walski TM, Chase DV, Savic DA (2001) Water distribution modeling. Haestad Press, Waterbury
Wood DJ, Charles COA (1972) Hydraulic network analysis using linear theory. J Hydraul Div 98:1157–1170
Acknowledgements
The financial support from the Centre for Science and Technology of the Non-aligned and Other Developing Countries (NAM S&T Centre) is gratefully acknowledged. Also, the authors extend their thanks to Professor E. Creaco for his valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hafsi, Z., Elaoud, S., Mishra, M. et al. Automated Framework for Water Looped Network Equilibrium. Water Resour Manage 32, 641–657 (2018). https://doi.org/10.1007/s11269-017-1831-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-017-1831-2