Skip to main content

Advertisement

SpringerLink
Log in

An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

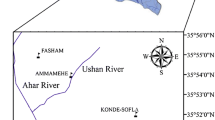
Sediment transport in streams and rivers takes two forms as suspended load and bed load. Suspended load comprises sand + silt + clay-sized particles that are held in suspension due to the turbulence and will only settle when the stream velocity decreases, such as when the streambed becomes flatter, or the streamflow into a pond or lake. The sources of the suspended sediments are the sediments transported from the river basin by runoff or wind and the eroded sediments of the river bed and banks. Suspended-sediment load is a key indicator for assessing the effect of land use changes, water quality studies and engineering practices in watercourses. Measuring suspended sediment in streams is real sampling and the collection process is both complex and expensive. In recent years, artificial intelligence methods have been used as a predictor for hydrological phenomenon namely to estimate the amount of suspended sediment. In this paper the abilities of Support Vector Machine (SVM), Artificial Neural Networks (ANNs) and Adaptive Network Based Fuzzy Inference System (ANFIS) models among the artificial intelligence methods have been investigated to estimate the suspended sediment load (SSL) in Ispir Bridge gauging station on Coruh River (station number: 2316). Coruh River is located in the northern east part of Turkey and it is one of the world”s the fastest, the deepest and the largest rivers of the Coruh Basin. In this study, in order to estimate the suspended sediment load, different combinations of the streamflow and the SSL were used as the model inputs. Its results accuracy was compared with the results of conventional correlation coefficient analysis between input and output variables and the best combination was identified. Finally, in order to predict SSL, the SVM, ANFIS and various ANNs models were used. The reliability of SVM, ANFIS and ANN models were determined based on performance criteria such as Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Efficiency Coefficient (EC) and Determination Coefficient (R2).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Afan HA, El-Shafie A, Yaseen ZM, Hameed MM, Wan Mohtar WHM, Hussain A (2015) ANN based sediment prediction model utilizing different input scenarios. Water Resour Manag 29:1231–1245

    Article  Google Scholar 

  • Alp M, Cigizoglu HK (2007) Suspended sediment load simulation by two artificial neural network methods using hydrometeorological data. Environmental Modeling and Software 22:2–13

    Article  Google Scholar 

  • Broomhead D, Lowe D (1988) Multivariable functional interpolation and adaptive networks. Complex Systems 2(6):568–576

    Google Scholar 

  • Caudill M, Butler C (1992) Understanding neural networks: 1 basic networks. The MIT Press, Cambridge

    Google Scholar 

  • Chong EKP, Zak SH (1996) An introduction to optimization. John Wiley&Sons, Inc

  • Cigizoglu HK (2003) Estimation, forecasting and extrapolation of river flows by artificial neural networks. Hydrological Sciences 48(3):349–361

  • Cigizoglu HK, Alp M (2005) Generalized regression neural network in modelling river sediment yield. Adv Eng Softw 37:63–68

    Article  Google Scholar 

  • Cigizoglu HK, Kisi O (2006) Methods to improve the neural network performance in suspended sediment estimation. J Hydrol 317(3–4):221–238

    Article  Google Scholar 

  • Dawson CW, Wilby RL (1998) An artificial neural network approach to rainfall –runoff modeling. Hydrol Sci J 43(1):47–66

    Article  Google Scholar 

  • Dawson CW, Wilby RL (2001) Hydrological modelling using artificial neural networks. Prog Phys Geogr 25:80–108

    Article  Google Scholar 

  • Demirel O, Kakilli A, Tektaş M (2010) ANFIS ve ARMA modelleri ile Elektrik enerjisi yük tahmini. Gazi Üniv Müh Mim Fak Dergisi 25(3):601–610 (in Turkish)

    Google Scholar 

  • Dogan E (2009) Katı madde konsantrasyonunun yapay sinir ağlarını kullanarak tahmin edilmesi. İMO Teknik Dergi 302:4567–4582 (in Turkish)

    Google Scholar 

  • Ebtehaj I, Bonakdari H (2014) Performance evaluation of adaptive neural fuzzy inference system for sediment transport in sewers. Water Resour Manag 28:4765–4779

    Article  Google Scholar 

  • Ekici S (2007) Elektrik Güç Sistemlerinde Akıllı Sistemler Yardımıyla Arıza Tipi ve Yerinin Belirlenmesi. PhD Thesis. Fırat Üniversitesi. Fen Bilimleri Enstitüsü (in Turkish)

  • Goyal MK (2014) Modeling of sediment yield prediction using M5 model tree algorithm and wavelet regression. Water Resour Manag 28:1991–2003

    Article  Google Scholar 

  • Hassan M, Shamim MA, Sikandar A, Mehmood I, Ahmed I, Ashiq S, Khitab A (2015) Development of sediment load estimation models by using artificial neural networking techniques. Environ Monit Assess 187(11):686

    Article  Google Scholar 

  • Hoya T, Chambers JA (2001) Heuristic pattern correction scheme using adaptively trained generalized regression neural networks. IEEE Trans. on Neural Networks 12(1):91–100

    Article  Google Scholar 

  • Jang JSR (1993) ANFIS adaptive –network-based-fuzzy inference systems. IEEE trans. On. Systems, Man and Cybernetics 23(3):665–685

    Article  Google Scholar 

  • Jang JSR, Tsai C, Mizutani E (1997) Neuro- fuzzy and soft computing: a computational approach to learning and machine intelligence. Prentice-Hall, Inc., N.J

    Google Scholar 

  • Kisi O, Ozkan C, Akay B (2012a) Modeling discharge–sediment relationship using neural networks with artificial bee colony algorithm. J Hydrol 428–429:94–103

    Article  Google Scholar 

  • Kisi O, Dailr AH, Cimen E, Shiri J (2012b) Suspended sediment modeling using genetic programming and soft computing tecniques. J Hydrol 450-451:48–58

    Article  Google Scholar 

  • Kumar SA, Ojha C, Goyal M, Singh R, Swamee P (2012) Modeling of suspended sediment concentration at Kasol in India using ANN, fuzzy logic, and decision tree algorithms. J Hydrol Eng 17(3):394–404

    Article  Google Scholar 

  • Lafdani EK, Nia AM, Ahmadi A (2013) Daily suspended sediment load prediction using artificial neural networks and support vector machines. J Hydrol 478:50–62

    Article  Google Scholar 

  • Melesse AM, Ahmad S, McClaina ME, Wang X, Limd YH (2011) Suspended sediment load prediction of river systems: an artificial neural network approach. Agric Water Manag 98:855–866

    Article  Google Scholar 

  • Miller CB (1951) Analysis of flow–duration, sediment- rating curver method of conputing sediment yield. U.S. Department of Interior, Bureau of Reclamation Sedimantation, Denver, Colorado

  • Moller MF (1993) A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw 6:525–533

    Article  Google Scholar 

  • Moriasi DN, Arnold JG, Van Liew MW, Bingner RL, Harmel RD, Veith TL (2007) Model evaluation guidelines for systematic quantifi cation of accuracy in watershed simulations. Trans ASABE 50:885–900

    Article  Google Scholar 

  • Muftuoglu RF (1980) Akarsu Yapıları, Cilt 1. İTÜ İnşaat Fakültesi Matbaası, İstanbul (in Turkish)

    Google Scholar 

  • Nourani V, Alizadeh F, Roushangar K (2016) Evaluation of a two-stage SVM and spatial statistics methods for modeling monthly river suspended sediment load. Water Resour Manag 30:393–407

    Article  Google Scholar 

  • Ozturk F, Apaydin H, Walling DE (2001) Suspended sediment loads through flood events for streams of Sakarya Basin, Turkish J Eng Env. TÜBİTAK 25:643–650

    Google Scholar 

  • Paredes V, Vidal E (2000) A class-dependent weighted dissimilarity measure for nearest neighbor classification problems. Pattern Recogn Lett 21:1027–1036

    Article  Google Scholar 

  • Park J (2006) Uncertainty and sensitivity analysis in support vector machines: Robuts optimization and uncertain programming approaches, dissertation. Norman, Oklahoma

    Google Scholar 

  • Partal T, Cigizoglu HK (2008) Estimation and forecasting of daily suspended sediment data using wavelet-neural network. J Hydrol 358:317–331

    Article  Google Scholar 

  • Salat R, Osowski S (2004) Accurate fault location in the power transmission line using support vector machine approach. Power Systems IEEE Transactions on 19:879–886

    Article  Google Scholar 

  • Sen Z (2004) Yapay Sinir Ağı İlkeleri. İstanbul, Su Vakfı Yayınları (in Turkish)

    Google Scholar 

  • Shepherd AJ (1997) Second-order methods for neural networks. Springer Verlag London Ltd.

  • Singh A, Imtiyaz M, Isaac RK, Denis DM (2013) Comparison of artificial neural network models for sediment yield prediction at single gauging station of watershed in eastern India. J Hydrol Eng 18(1):115–120

    Article  Google Scholar 

  • Sivakumar B (2006) Suspended sediment load estimation and the problem of inadequate data sampling: a fractal view. Earth Surf Process Landf 31:414–427

    Article  Google Scholar 

  • Skapura DM (1996) Building neural networks. Addison-Wesley, New York

    Google Scholar 

  • Specht DF (1991) General regression neural network. IEEE Trans on Neural Networks 2(6):568–576

  • Vapnik V (1995) The nature of statistical learning theory. Springer, New York

    Book  Google Scholar 

  • Verleysen M, Hlavackova K (1994) An optimized RBF network for approximation of functions. Proceedings European Symposium on Artificial Neural Networks. Brussels, Belgium, pp 175–180

    Google Scholar 

  • Yang CT (1996) Sediment transport theory and practice. McGraw-Hill, USA

    Google Scholar 

  • Yanmaz M, Kumcu SY (2007) Measurement of sediment load. Post-graduate course in sediment transport technology. DSI press, Ankara

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, University of Selcuk, Konya, Turkey

    Meral Buyukyildiz

  2. Department of Civil Engineering, University of Necmettin Erbakan, Konya, Turkey

    Serife Yurdagul Kumcu

Authors
  1. Meral Buyukyildiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Serife Yurdagul Kumcu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Meral Buyukyildiz.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buyukyildiz, M., Kumcu, S.Y. An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models. Water Resour Manage 31, 1343–1359 (2017). https://doi.org/10.1007/s11269-017-1581-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-017-1581-1

Keywords

Search

Navigation