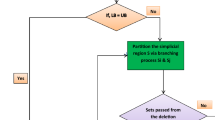
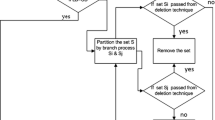
We study the solution of a multiobjective nonlinear sum of fractional optimization problems. A dualitybased branch and bound cut method is developed for the efficient solution of this problems. The proposed methodology is validated by proving the required theoretical assertions for the solution. The present method is an extension of the work P. P. Shen, Y. P. Duan, and Y. G. Pei [J. Comput. Appl. Math., 223, 145–158 (2009)] developed for a single-objective sum of ratios of nonlinear optimization problems. The proposed method is realized in MatLab (version 2014b). Two numerical problems are considered and solved by using the proposed method and the global optimal solution is obtained.
Similar content being viewed by others
References
F. H. Mathis and L. J. Mathis, “A nonlinear programming algorithm for hospital management,” SIAM Rev., 37, 230–234 (1995).
S. Schaible, “A note on the sum of a linear and linear fractional functions,” Naval Res. Logist., 24, 61–963 (1977).
H. P. Benson, “Global optimization algorithm for the nonlinear sum of ratios problem,” J. Math. Anal. Appl., 263, 301–315 (2001).
H. P. Benson, “Global optimization algorithm for the nonlinear sum of ratios problem,” J. Optim. Theory Appl., 112(1), 1–129 (2002).
H. P. Benson, “Generating sum of ratios test problems in global optimization,” J. Optim. Theory Appl., 119(3), 615–621 (2003).
H. P. Benson, “On the global optimization of sums of linear fractional functions over a convex set,” J. Optim. Theory Appl., 121(1), 19–39 (2004).
H. P. Benson, “A simplicial branch and bound duality-bounds algorithm for the linear sum-of-ratio problem,” Eur. J. Oper. Res., 182, 597–611 (2007).
H. P. Benson, “Solving sum of ratios fractional programs via concave minimization,” J. Optim. Theory Appl., 135, 1–17 (2007).
H. P. Benson, “Branch and bound outer approximation algorithms for sum-of-ratios fractional programs,” J. Optim. Theory Appl., 146, 1–18 (2010).
C. H. Scott and T. R. Jefferson, “Duality of nonconvex sum of ratios,” J. Optim. Theory Appl., 98(1), 151–159 (1998).
P. Shen and L. Jin, “Using canonical partition to globally maximizing the nonlinear sum of ratios,” Appl. Math. Model., 34, 2396–2413 (2010).
Y. J. Wang and K. C. Zhang, “Global optimization of nonlinear sum of ratios problem,” Appl. Math. Comput., 158, 319–330 (2004).
P. P. Shen and C. F.Wang, “Global optimization for sum of ratios problem with with coefficient,” Appl. Math. Comput., 176, 219–229 (2006).
H. Jiao and P. Shen, “A note on the paper global optimization of nonlinear sum of ratios,” Appl. Math. Comput., 188, 1812–1815 (2007).
S. J. Qu, K. C. Zhang, and J. K. Zhao, “An efficient algorithm for globally minimizing sum of quadratics ratios problem with nonconvex quadratics constraints,” Appl. Math. Comput., 189, 1624–1636 (2007).
P. Shen, Y. Chen, and M. Yuan, “Solving sum of quadratic ratios fractional programs via monotonic function,” Appl. Math. Comput., 212, 234–244 (2009).
P. Shen, W. Li, and X. Bai, “Maximizing for the sum of ratios of two convex functions over a convex set,” Comput. Oper. Res., 40, 2301–2307 (2013).
P. Shen and C. F. Wang, “Global optimization for sum of generalization fractional functions,” J. Comput. Appl. Math., 214, 1–12 (2008).
P. P. Shen, Y. P. Duan, and Y. G. Pei, “A simplicial branch and duality bound algorithm for the sum of convex-convex ratios problem,” J. Comput. Appl. Math., 223, 145–158 (2009).
M. Jaberipour and E. Khorram, “Solving the sum-of-ratios problem by a harmony search algorithm,” J. Comput. Appl. Math., 234, 733–742 (2010).
L. Jin and X. P. Hou, “Global optimization for a class nonlinear sum of ratios problems,” Math. Probl. Eng., Article ID: 103569 (2014).
Y. Gao and S. Jin, “A global optimization algorithm for sum of linear ratios problem,” J. Appl. Math., Article ID: 276245 (2013).
R. W. Freund and F. Jarre, “Solving the sum-of-ratios problem by an interior-point method,” J. Global Optim., 19, 83–102 (2001).
S. Schaible and J. Shi, “Fractional programming: the sum-of-ratio case,” Optim. Methods Softw., 18(2), 219–229 (2003).
J. G. Carlsson and J. Shi, “A linear relaxation algorithm for solving the sum of linear ratios problem with lower dimension,” Oper. Res. Lett., 41, 381–389 (2013).
A. M. Ashtiani and A. V. Ferreira, “A branch and cut algorithm for a class of sum of ratios problems,” Appl. Math. Comput., 268, 596–608 (2015).
R. Horst and H. Tuy, Global Optimization: Deterministic Approaches, Springer, Berlin (1996).
Author information
Authors and Affiliations
Additional information
Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 69, No. 11, pp. 1455–1471, November, 2017.
Rights and permissions
About this article
Cite this article
Bhati, D., Singh, P. Multiobjective Nonlinear Sum of Fractional Optimization Problems with Nonconvex Constraints with the Use of the Duality-Based Branch and Bound Algorithm. Ukr Math J 69, 1689–1709 (2018). https://doi.org/10.1007/s11253-018-1464-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-018-1464-5