1 Introduction

Polymer electrolyte fuel cells (PEFCs) are used in an increasing set of applications. There is still demand for optimizing components with respect to efficiency and durability. One component with a large influence on efficient fuel cell operation is the gas diffusion layer (GDL), especially its properties that affect the transport of liquid water which is produced on the cathode side. GDLs for fuel cells (FC) are porous layers of 200–300 μm thickness, typically made of carbon fibers. Without further treatment the fibers are hydrophilic, and a porous micro-structure made from pure carbon fibers would absorb liquid water when it enters the GDL. As a result, any paths for oxygen to be passed in counter flow would be blocked. For this reason, GDLs are treated with hydrophobic coatings, typically polytetrafluorethylene (PTFE). GDLs are sold by manufacturers with a given total amount of PTFE, often without specification of the positions where the PTFE is located inside the micro-structure. On the other hand, it is known that the distribution of PTFE can change with manufacturing conditions as shown by Hartnig et al. (2008).  Fishman and Bazylak (2011) observed a through-plane distribution of PTFE where the PTFE was concentrated at the outer regions of different types of GDL. Mendoza et al. (2011) visualized PTFE in fiber-based GDLs. They observed local agglomerates of PTFE inside the micro-structure depending on the manufacturing process. Ince et al. (2020) analyzed GDLs by means of in-situ X-ray tomography, identifying the local positions of liquid water, fibers, PTFE and void space. Furthermore, the GDL, micro porous layer (MPL) and catalyst layer (CL) regions were identified. Chen et al. (2018) assembled several cell configurations and varied the PTFE coating in the anode and cathode GDL. When the cells were operated under different conditions, the anodic PTFE content for the transport of liquid water was observed to be highly relevant. Meanwhile, experiments conducted by Chen et al. (2019) also addressed PTFE content in the GDL. Its influence on the thermal conductivity of the GDL and FC performance was investigated. Truong et al. (2018) studied the impact of PTFE on the performance of a PEFC by tuning the PTFE content in the GDL. They analyzed the structural properties of the GDL and catalyst layer surface. The impact of the total amount of PTFE on the efficiency of fuel cells was investigated by Omrani and Shabani (2019) when they operated an unitized regenerative fuel cell in FC-mode. They operated their stacks under different temperatures and different humidity conditions. Laoun et al. (2018) systematically operated PEFCs with different kinds of GDLs under various conditions using Design of Experiments (DOE) to analyze the amount of PTFE on FC performance. Recently,  Balzarotti et al. (2020) prepared GDLs with a hydrophobic perfluorpolyether-based polymer which was found to be more efficient than PTFE.

The relevance of PTFE to the micro-structure of GDLs is reflected by a variety of investigations. An overview of the modeling investigations of structural inhomogeneties of the micro-structure of different types of GDLs was presented by García-Salaberri et al. (2019). Molaeimanesh and Akbari (2016), in turn, analyzed the relationship between the wettability of the porous material of a GDL and the size of liquid water droplets transported through it. Their lattice Boltzmann (LB) simulations showed the necessity of either sufficiently high hydrophobicity of the GDL or small droplets. The detailed movement of droplets in fibrous materials was experimentally analyzed by Aslannejad et al. (2018), who also simulated water transport through the GDL by means of computational fluid dynamic (CFD) using the OpenFOAM software. Mortazavi and Tajiri (2013) analyzed the Toray GDL of different types and levels of PTFE coating regarding their contact angles at the GDL surface and the pore size distributions inside. Lin et al. (2019) demonstrated experimentally the relevance of contact angles for fuel cell efficiency. Meanwhile, Yu et al. (2018a) and Froning et al. (2019) simulated liquid transport in GDL using the LB method and presented statistical distributions of contact angles, mainly influenced by the irregular geometry of the individual pores. The contact angles of fresh and aged GDLs on the anode and cathode sides of a fuel cell were measured by Planes et al. (2018). The influence of the distribution of PTFE in the 3D micro-structure of a GDL was investigated by Yu et al. (2019), Chen and Jiang (2016), Niu et al. (2018), and also by Kakaee et al. (2018). These researchers analyzed the uniform and non-uniform distributions of PTFE in the fiber structure of paper-type GDLs. In this context, the macroscopic PTFE distribution can be seen in layers with different PTFE concentrations. Shakerinejad et al. (2018) studied GDL performance with the presence of hydrophilic layers inside, using the LB method for their simulations. Tavangarrad et al. (2018) experimentally investigated the redistribution of PTFE in a situation where two thin layers of different hydrophobicity were stacked upon each other. Ito et al. (2016) applied PTFE to Toray 090 GDLs using different techniques. With energy-dispersive X-ray spectroscopy (EDS) imaging they observed homogeneous and one-sided inhomogeneous PTFE profiles, depending on the method. The hydrophobicity of porous materials is also important for other applications. Lee and Huang (2019) also investigated hydrophobic GDLs for electrochemical hydrogen pumps.

The characteristics of the liquid flow influences macroscopic transport in the gas channels of a PEFC, especially on the cathode side where liquid water must be transported out of the fuel cell. One important feature is the contact angle of liquid water on the rough GDL surface. Andersson et al. (2018a, b) demonstrated the high relevance of the contact angle in their simulations of droplet detachment in the cathode channel of a PEFC. In volume of fluid (VOF) simulations they used the contact angle as a model parameter to specify the surface tension between the liquid water and rough surface of the GDL. Subsequently, they elaborated a more accurate VOF model that uses two contact angles for this purpose (Andersson et al. 2019). At the same time Malhotra and Gosh (2018) simulated water transport in the serpentine channel of a PEFC by means of CFD. Unlike the studies mentioned above, Hou et al. (2018) used the LB method for the simulation of such problems, investigating the coalescence of droplets in the air channel of a fuel cell.

Fig. 1
figure 1

Overview of the paper

Full size image

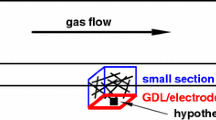
In this work, the influence of PTFE is investigated from three viewpoints, as sketched out in Fig. 1. A local PTFE distribution model is introduced that considers fiber crossings as the preferred locations wherein PTFE is deposited onto the fibers of the micro-structure. The global distribution of PTFE along the through-plane direction is analyzed with regard to the time needed for transporting liquid water through the GDL. Both distribution models are analyzed in terms of the time how long liquid water needs to be transported through the GDL. Special attention is given to the role of the last fiber layer and its significance to the characteristics of the droplets leaving the GDL. The manuscript is a continuation of our previous work (Yu et al. 2019) where an impact of the PTFE distribution on liquid water transport was already found.

2 Methods

2.1 Geometry Model

In this section, the geometry model is illustrated with a focus on the PTFE distribution models in Sect. 2.1.2 which are more detailed than in our previous work (Yu et al. 2019).

2.1.1 Fiber Model

The geometry of Toray 090 GDL is represented by a stochastic model developed by Thiedmann et al. (2008). Using a 2D scanning electron microscopy (SEM) image the fibers were identified. The top layer of this system of fibers was extracted according to the number of fiber crossings of the lines in the image. These top-level lines were then used to determine a particular class of Poisson line tesselations. The lines were dilated to cylinders with a fiber diameter of 7.5 μm to create a 3D structure of a representation of the GDL. According to the known porosity of the GDL, the missing amount of binder was statistically added by Thiedmann et al. (2009). The representations of the 3D structure created in this manner were validated against the real structure obtained from the BESSY synchrotron in Berlin, Germany. The fiber model, including the binder, was the geometric basis for the previous work of Froning et al. (2013, 2014, 2018a, b) and Yu et al. (2018a, b, 2019).

In this work, the PTFE distribution in the micro-structure is analyzed not only with respect to its impact on the local surface tension of the liquid water; the change of local porosity is also considered. For this reason, the fibers without the binder were chosen as the basis for the micro-structure. For each fiber layer the fibers are given as a set of lines, represented in Hesse normal form, as described by Thiedmann et al. (2008). To create a 3D structure the lines are dilated. According to a lattice with a 1.5 μm voxel size, each set of lines is dilated to five image layers. As above, a square cross-section of the fibers was chosen. In this way, 26 fiber layers are represented by 130 images. With an image size of \(512 \times 512\), a GDL section of \(756\,{\upmu \hbox {m}} \times 756\,{\upmu \hbox {m}}\) and \(195\,{\upmu \hbox {m}}\) thickness is specified. This skeleton of fibers is completed with a PTFE covering that changes the surface tension of the liquid water at the fiber surface. The porosity of the porous layer is also decreased.

To avoid interference between the geometry and fiber models, only one representation of the stochastic fiber model was selected for this work. In total, 1204 fibers are placed in the 26 layers, with the number of fibers per layer ranging from 34 to 67.

2.1.2 PTFE Model

In two-phase simulations of previous work (Yu et al. 2018a, b, 2019), PTFE was considered as a surface characteristic of the fibers. On the other hand, it is known that manufacturers add PTFE in total mass fractions of 10%, 20%, or 30% which also changes the porosity of the material. In this work, the PTFE was deposited at the fiber structure in accordance with three approaches:

  • Local PTFE distribution model: this addresses how the PTFE is placed in the fibers and the choice of local positions.

  • The global PTFE distribution specifies the through-plane distribution of the PTFE across the fiber layers.

  • The last fiber layer can be covered by additional PTFE in order to control the shape of liquid water droplets on the GDL surface.

The method for adding PTFE to the fibers differs from the algorithm presented by Yu et al. (2019). In previous work (Yu et al. 2019), the location of the PTFE was established as a surface characteristic of the fibers. The volume change of the added PTFE was neglected. This assumption was made because the underlying geometry model included a binder that was adjusted to meet the known porosity of the fiber structure (Thiedmann et al. 2009; Froning et al. 2013).

In the present work, the same fiber model was used but without the binder. For this reason, the pure fibers as introduced by Thiedmann et al. (2008) were taken as the basis for this manuscript. The PTFE added to the fibers changes the porosity of the GDL. The GDL material can usually be ordered with different amounts of PTFE added to the fibers, typically given in volume fractions. Yu et al. (2019) estimated cover fractions of up to 100% related to 27% weight fraction of PTFE in their simplified surface based PTFE model. In this work, the PTFE was added in volume fractions of 4%, 6% and 8%, according to the loss of porosity, by adding PTFE. Based on 80% porosity, \(\rho _{\text {carbon}}=2\,\text {g}\,\text {cm}^{-3}\) and \(\rho _{\text {PTFE}}=2.2\,\text {g}\,\text {cm}^{-3}\), this corresponds, respectively, to an 18%, 27%, and 36% mass fraction.

Local PTFE distribution model

The PTFE is added to the micro-structure based on its representation on the lattice. This leads to a coarse approximation of the PTFE distribution depending on the resolution of the lattice, as already noted by Yu et al. (2019). According to visualizations by Chen and Jiang (2016), the PTFE is assumed to concentrate near fiber crossings. The PTFE model described in this manuscript randomly selects a location where two fibers touch each other and then covers the fibers inside a certain region around the crossing point. This is shown schematically in Fig. 2a. The PTFE distribution is further tuned by two stochastic sub-models. A global sub-model \(M_1\) selects the strategy to distribute the PTFE globally and affects the choice of the fiber crossing to begin with a local PTFE covering. A second sub-model \(M_2\) specifies the size of the region around the fiber crossing. This roughly corresponds to the size of agglomerates observed by Mendoza et al. (2011). Indirectly, the parameters of \(M_2\) also influence the number of crossing points to be chosen to achieve the total amount of PTFE to be added to the GDL. Figure 2b illustrates how this is applied to a fiber layer.

Fig. 2
figure 2

Local deposition of PTFE; a PTFE covering the fibers near a fiber crossing; b PTFE in one fiber layer of the GDL

Full size image

Global PTFE distribution model

The global distribution of PTFE in the through-plane direction can be specified either as uniform—this is called mode G1 in this work—or non-uniform with the PTFE preferably distributed in the outer regions of the GDL—which are modes G2 or G3. In mode G1 the random function was extended by the factor \((L+2)\) instead of the number of image layers L to avoid an undesired bending of the Java implementation near the boundary values (0, 1). The non-uniform distribution (modes G2, G3) is implemented using the Gaussian function. The resulting index layer \(i_L\) shown in Table 1 is cut off at the index boundaries. For mode G3, the left and right side of the Gaussian function is alternated to ensure the same amount of PTFE on each side of the GDL. The basic idea is to put a certain amount of PTFE into the GDL. The concept of distributing 50% PTFE across the GDL is illustrated in Fig. 3a. The influence of this kind of global distribution was already presented by Yu et al. (2019). In this work, the non-uniform PTFE distributions are implemented more smoothly by applying normal distribution functions whose mean value is at the outer regions of the GDL. The statistical densities of the three modes are shown in Fig. 3b.

Fig. 3
figure 3

Global distribution of PTFE in the through-plane direction of the GDL; a basic idea of the modes; b distribution functions

Full size image

The G2 mode preferably puts the PTFE into the outer regions of the GDL. This represents the inhomogeneous distribution influenced by the drying method during the manufacturing process as described by Ito et al. (2014). Yu et al. (2019) identified a one-sided inhomogeneous PTFE distribution in the upstream region of the GDL as being desirable for fast water transport through the GDL. This is taken into account in our study as mode G3.

The local PTFE model determines the amount of PTFE deposited in the region around selected crossing points. This is also performed by a stochastic model, as specified below.

  1. 1.

    Determine all fiber crossings. Approximately 40,000 positions were identified in the given example. Fiber crossings inside one layer are considered, as well as the crossings of fibers from two neighboring layers. Without consideration of the neighboring layers, only 20,000 crossings would be available.

  2. 2.

    Calculate the total number of void voxels near the fibers to convert to PTFE. For example, 6% of a \(512 \times 512 \times 130\) lattice yields 2,044,723 voxels to convert. This would result in approximately \(p_0=51\) voxels per fiber crossing based on a completely homogeneous distribution on the global scale. This number \(p_0\) is the base parameter for the individual number \(p_i\) of voxels converted to PTFE around a selected fiber crossing (number i in the next steps).

  3. 3.

    Randomly select a fiber crossing. According to the global PTFE distribution model, it can be selected with a uniform distribution or preferably on one or both outer regions in the through-plane direction.

    1. (a)

      Select a fiber layer according to the global PTFE model.

    2. (b)

      Randomly select a crossing point inside the fiber layer. The intersections between two neighboring fiber layers are assigned to the lower one.

  4. 4.

    Determine the individual number of voxels to be converted with respect to the local PTFE model according to Eq. (1).

    $$\begin{aligned} p_i=p_0 \cdot (c_1+c_2 \cdot \text {random}()) \end{aligned}$$
    (1)
  5. 5.

    Convert \(p_i\) voxels around the fiber crossing.

  6. 6.

    Repeat steps 3–5 until the total number of PTFE voxels is reached.

  7. 7.

    Additional PTFE is applied to the top fiber layer for certain configurations introduced in Sect. 3.

The parameters of the local PTFE model depend strongly on the resolution of the lattice. In this work, the parameters from Table 1 were chosen. With the choice of \(c_1\) and \(c_2\), Eq. (1) leads to a stochastically generated subset of the 40,000 fiber crossings.

Table 1 Parameters of the PTFE distribution models
Full size table

For each crossing point i of the fibers, a number of \(p_i\) PTFE voxels are attached to them. Starting at the position of the crossing point, a surrounding region is defined as the set of voxels around the starting point. Inside this region, the fibers are covered with PTFE. The regions are extended stepwise along the fibers until the amount of PTFE exceeds \(p_i\). Figure 2b shows the result for one fiber layer. As the fibers are covered with PTFE outside of the solid structure, the 130 images of the GDL are extended to 132 images to represent the PTFE under the first and above the top fiber layers.

The choice of parameters \(c_1\) and \(c_2\) from Table 1 indirectly determines the total number of fiber crossings that are selected for the PTFE deposition. In Eq. (1), parameter \(p_0\) specifies the number of pixels to be converted if the chosen amount of PTFE was distributed completely homogeneously to all fiber crossings. The average value of \(1/p_i\) therefore denominates the ratio of fiber crossings selected for PTFE deposition. As a result, the local PTFE distribution model with parameters \(c_1\) and \(c_2\) from Table 1 depends strongly on the chosen lattice. Although the local and global PTFE distribution models are discussed separately, they are not independent of each other. This will be clarified in Sect. 3.

PTFE at the last fiber layer

The PTFE distribution models mentioned above also place some PTFE at the last fiber layer where the liquid water leaves the GDL. Because the contact angle was identified as a remarkable property of the rough GDL surface by Yu et al. (2018a), the influence of PTFE on the last fiber layer was investigated in this work. Three approaches have been analyzed schematically, as is shown in Fig. 4.

Fig. 4
figure 4

Cross-section of a fiber in the top layer. Liquid water is moving in an upward direction. a Mode F1: without special treatment; b Mode F2: PTFE covering the top image layer; c Mode F3: PTFE covering the top fiber layer

Full size image

The figure shows a cross-section of a fiber at a position where a fiber of the top layer is not covered with PTFE in addition to the previous distribution algorithm. Figure 4a represents the situation after distributing the PTFE according to the local and global PTFE distribution models mentioned above. The fibers are covered with PTFE by the stochastic algorithm. Some regions of the topmost fibers are not covered with it though. The two approaches shown in Fig. 4b, c consider the entire fiber layer covered with additional PTFE in order to enlarge the contact angles on the GDL surface.

One approach is to place PTFE in one image layer along the fibers. From the viewpoint of liquid water passing upwards through the GDL, this PTFE is located behind the fibers (Fig. 4b). The other approach is to cover the fibers on three of the four sides of the fiber. This is shown in Fig. 4c.

2.2 Lattice Boltzmann Method

Detailed transport simulations are performed using the lattice Boltzmann method (LBM). Based on gas kinetics, ensembles of multiple molecules are handled statistically (Succi 2001). The Boltzmann equation is as follows:

$$\begin{aligned} \frac{\partial f}{\partial t} + v \nabla f = Q\ \end{aligned}$$
(2)

with the probability function f, velocity v and collision integral Q being simplified according to some assumptions. On a regular lattice,

$$\begin{aligned} f_{\mathbf{x},i}, i=0, \ldots , 18, \end{aligned}$$
(3)

defines the D3Q19 scheme. Here, \(f_\mathbf{x},i, i=0, \ldots , 18\) denominate the probabilities of a molecule moving from position \(\mathbf{x}\) on the 3D lattice to position \(\mathbf{x}+\xi _i, i=0, \ldots , 18\) in a fixed time step \(\delta _t\), \(\xi _i\) are defined as vectors on an equidistant lattice that is defined by the geometry given as image series, as specified in Sect. 2.1.1.

As long as the \(f_i\) are not too far from the equilibrium—this is ensured for \(Ma \ll 1, Kn \ll 1\) (Brinkmann et al. 2012; Succi 2001)—the system can be iteratively solved. For each phase \(\sigma = 1,2\) a system of \(f^\sigma\) is specified according to Eq. (3). For numerical robustness the multiple relaxation time (MRT) was used (Yu et al. 2018a) and the two phases are coupled by means of the Shan Chen approach (Shan and Chen 1993).

It was shown by Sakaida et al. (2017), as well as Yu et al. (2018a), that such two-phase transport simulations in porous media are valid for capillary numbers of up to \(10^{-3}\).

According to Yu et al. (2018a), the PTFE is considered by the adhesion force in the Shan Chen two-phase model. The corresponding adhesion parameters \(G_\text {adh}^\sigma\) for the fluid phases \(\sigma =1,2\) lead to a certain contact angle of a liquid droplet on a flat surface when no other forces are present. In this way, local contact angles were implemented as surface characteristics of the fibers—whether they are covered with PTFE or not. As in our previous work, presented by Yu et al. (2019), the local contact angle is 120\({}^\circ\) in the presence of PTFE and 90\({}^\circ\) on carbon—related to the flat surface. The adhesion parameters were chosen accordingly.

2.3 Post-processing

The simulation results were analyzed with respect to two characteristics: the breakthrough time of the droplet passing through the GDL and the contact angle of the droplet upon the rough GDL surface. The breakthrough time was already presented by Yu et al. (2019). It is determined by the change in the slope of the saturation curve over time.

The second property to be analyzed is the contact angle. The shape of the droplets leaving the GDL was characterized by their contact angles which were calculated using the sub-pixel polynomial fitting (SPPF) method as introduced by Yu et al. (2018a) and Froning et al. (2019).

  1. 1.

    In the first step, a straight line is fitted to n points near the contact boundary of the GDL surface. Its intersection with the GDL surface—which is a virtual post-processing line—is the particular coordinate \((x_0,y_0)\) that represents the contact point where the droplet cuts across the GDL surface. In Fig. 5 the contact boundary is located at \(y_0=0\).

  2. 2.

    A second-order polynomial constrained through the contact point is fitted through m points.

  3. 3.

    The gradient of the polynomial at the contact point defines the contact angle.

The application of the SPPF method is illustrated in Fig. 5.

Fig. 5
figure 5

Application of the SPPF method, a on the left side of a vertical cut of a droplet, b on the right side

Full size image

The black points in the figure are the shape of a vertical cut of a droplet, as exported from Paraview(Kitware 2009). In particular, the data of droplet No. 1 from Fig. 13c were taken into account for this evaluation. The shape was evaluated in the region above the GDL surface which in fact is merely a post-processing plane. Only the lower points of the curve can be evaluated, as displayed in the lower-left part of Fig. 5a and the lower-right part of Fig. 5b. It can be seen that only a small amount data is eligible for the approximation of simple functions. The number of eligible points strongly depends on the resolution of the lattice, but also of the particular post-processing steps in Paraview, namely the number of points exported to the SPPF method. From the present simulations, \(n=5\) and \(m=12\) were chosen for the evaluation of the contact angles. The red line is the straight line fitted through \(n=5\) points, while the blue line is the constrained polynomial. The contact angle is the slope of the green line, which is the gradient of the second-order polynomial at the contact point \((x_0,y_0)\). It can be seen that it sometimes differs significantly from the straight-line approximation, e.g., in Fig. 5b.

3 Simulation Setup

The micro-structure for the LB simulations is created from a representation of the stochastic fiber model. Only one fiber representation is chosen to avoid interference with the PTFE distribution model. The PTFE distribution was configured in the set of configurations shown in Table 2. Configuration F is introduced to provide more realistic contact angles; see Mortazavi and Tajiri (2013) and Lin et al. (2019).

Table 2 Configurations of the PTFE distribution
Full size table

3.1 Local PTFE Distribution Setup

The configurations A-C correspond to modes L1-L3 of the local PTFE distribution in Table 1 and mode G1 of the global PTFE distribution. Configurations D and E represent modes G2 and G3 of the global PTFE distribution. They are based on the most promising results from our previous work (Yu et al. 2019). The base configurations A-E were configured with 6% PTFE in total, as well as with 8% PTFE. Each configuration was generated in six representations. The local PTFE distribution of configurations A-C was calculated using the parameters from Table 1. The sandwiched configuration (E) relates to—but is not the same as—the hydrophilic layer shown by Shakerinejad et al. (2018). Based on the scheme of positioning the PTFE near fiber crossings, as shown in the image series in Fig. 6a, the micro-structure is transferred via a series of images—one of them shown in Fig. 6b—to the LB simulation framework.

Fig. 6
figure 6

PTFE distribution with the PTFE in red. a Stack of an image series with PTFE; b 3D view of the micro-structure

Full size image

The implementation of the uniform PTFE distribution is shown in Fig. 7a–c for 8% PTFE, the parameters of the local PTFE distribution being applied according to Table 1. A total of 6% PTFE, related to the total volume of the GDL, leads to 24.3% PTFE, related to the volume of the fibers. As the density of PTFE and carbon are close to each other—\(\rho _{\text {carbon}}=2\,\text {g}\,\text {cm}^{-3}\), \(\rho _{\text {PTFE}}=2.2\,\text {g}\,\text {cm}^{-3}\)—the volume fraction of PTFE in the GDL is close to the weight fraction: \(24.3\% \cdot (2.2 / 2.0) = 26.7\%\). For 8% PTFE (total) the volume fraction is 32.3% and the weight fraction 35.5%. While GDL manufacturers specify the PTFE in terms of weight fractions, care must be taken when the amount of PTFE is specified, as the volume or weight fraction in a geometry model based on coarse grids is used in these simulations. Yu et al. (2019) presented a relationship between the weight fraction of the PTFE and cover fraction—the amount of fiber surface covered with PTFE. They assumed smooth cylindrical fibers covered with a homogeneous film of PTFE, thinner than the resolution of the coarse grid. In the LB algorithm, the influence of the PTFE on the fluid flow is implemented via the surface characteristics, related to boundary conditions at the fiber surface. The grid-based cover fraction of the PTFE is specified in Table 3. These numbers are to be used when the results of the present work are compared with previous results that were based on cover fractions (Yu et al. 2019).

Table 3 Grid-based cover fraction/% of PTFE at the carbon fibers
Full size table

3.2 Global PTFE Distribution Setup

The setup number (setup No. in Table 3) is composed of the global PTFE distribution model (A to E) and the PTFE fraction, related to the total volume (6% or 8%). There is a statistical variation in the cover fraction in ensembles v0 to v5 of every global PTFE setup number. For the setup numbers D.6 and D.8—the one-sided inhomogeneous distribution—the PTFE cover fraction is slightly lower than the others. Although it is unusual to relate the PTFE to the total volume, this nomenclature was chosen to avoid confusion when the results are compared to surface-based simulations, e.g., by Yu et al. (2019)—their cover fractions range from 25 to 50%.

Fig. 7
figure 7

Through-plane distribution of 8% PTFE on 26 fiber layers, six stochastic representations each configuration A–E of Table 2. Top row: uniform distribution, a mode L1; b mode L2; c mode L3. Bottom row: non-uniform distribution, d one-sided; e sandwiched

Full size image

The non-uniform PTFE distribution with local parameters according to mode A are shown in Fig. 7d, e.

The through-plane profiles presented in Fig. 7 show fluctuations that overlay the idealized curves from Fig. 3b. The profiles were calculated by counting red pixels in the series of images. In Fig. 6b, the PTFE is represented in red in the images. Five images represent one fiber layer—except for the bottom and top ones. The bottom fiber layer with index 0 also covers the PTFE underneath the GDL, and therefore six image layers are summarized instead of five. The same systematic applies to the top fiber layer with index 25. This affects all profiles in Fig. 7, as sharp upward kinks at the outer positions at layers 0 and 25. Large fluctuations are also promoted by the coarse through-plane grid: there are only 26 fiber layers, consisting of stochastically generated sets them. The differences in the geometries is indicated by fluctuations in the through-plane PTFE distribution.

3.3 Top Fiber Layer

The PTFE affects the 3D transport of liquid water in the micro-structure. There are measurable characteristics on the GDL surface, one of which is the macroscopic contact angle of water droplets on the rough GDL surface. One configuration of the local and global PTFE models was selected for a variation in the top fiber layer’s handling. In this way, interference between the PTFE distribution models and treatment of the top fiber layer is avoided.

The difference is illustrated schematically in Fig. 4. Figure 4a represents the situation for configurations A–E. Particularly in configuration D, large regions of the topmost fibers are not covered with PTFE. Two approaches are shown in Fig. 4b, c: In (b) additional PTFE is added at the image layer above the fibers, and (c) considers three quarters of the fiber surface covered with additional PTFE.

3.4 Simulation Frame

The transport of liquid water is simulated in a frame, as depicted in Fig. 8. Like in our previous work (Yu et al. 2018a, b, 2019), the space below the GDL is initially filled with water, the other open space is filled with air. The simulation frame consists of the GDL, as illustrated in Fig. 6 and the PTFE distributed by the stochastic approaches mentioned above. The nodes of the GDL micro-structure are read as image series with three colors, two of them specifying either carbon or PTFE material of the solid phase as illustrated in Fig. 2. Below, there is a small region—10 image layers—to allow for consistent boundary conditions at the inlet. Above the GDL there is free space to allow the liquid water droplet to leave the rough GDL surface. The fluid-solid boundary of the fibers is implemented as bounce-back boundary condition with the adhesion force of the Shan Chen model implemented on top as described in Sect. 2.2. While the porous micro-structure of the GDL is not periodic, periodic boundary conditions were applied at the side boundaries. This ensures that the shape of droplets leaving the GDL are not affected by the boundary conditions. The velocity of the liquid water entering the upstream region was chosen to specify a capillary number of \(10^{-4}\). These are the same boundary conditions as in our previous work (Yu et al. 2019).

Fig. 8
figure 8

Setup and boundary conditions for the LB simulation

Full size image

4 Results

The configurations in Table 2 were taken to create 12 stochastic representations of the PTFE distribution each, all of them following the same fiber geometry. Six representations, each with 6% PTFE were generated, as were six with 8% PTFE. Seven of these combinations were taken as the base for the succeeding LB simulations. Every configuration from Table 2 was chosen with 8% PTFE, while configuration D was also evaluated with 6% PTFE in the micro-structure. As in previous studies (Yu et al. 2018a, 2019; Froning et al. 2019), transport simulations were run for 60,000 time steps. Within this period, droplets emerged from the upper surface of the GDL after the liquid water was transported through the porous structure. As was introduced in Sect. 2.3, the slope of the saturation curve decreases as soon as the first water droplet leaves the GDL.

The transport simulation led to snapshots of the dynamic process of liquid water transport. The simulation time was chosen to ensure that at least one droplet emerged from the GDL surface in any case. Figure 9 shows three of the six simulations of configuration A.8 with 8% PTFE. Droplets (in blue) are emerging from the GDL surface at different positions and are of similar size in the three visualizations. At the upper fiber layers the PTFE is visible in red. The pattern changes from Fig. 9a–c.

Fig. 9
figure 9

Impact of the local PTFE distribution, configuration A.8 with 8% PTFE. Situation after 60,000 time-steps. a Representation 1 of 6. b Representation 2 of 6. c Representation 3 of 6

Full size image

The impact of the global PTFE distribution is shown in Fig. 10. Six representations were simulated for each configuration, only one of which is visualized. Configurations B and C in Fig. 10a, b do not look different from configuration A in Fig. 9. Several droplets (in blue) are emerging from the GDL surface at different positions. At the top fiber layer, the PTFE is clearly visible. With configuration D.8, the picture changes in two respects. The size of the droplets is larger in Fig. 10 c) and the PTFE hides in the lower regions of the GDL. In particular, almost no PTFE is visible at the top fiber layer, and the droplets show a flat shape. Not only the size, but also the positions where the droplets leave the GDL are affected by the PTFE distribution.

Fig. 10
figure 10

Impact of the global PTFE distribution; situation after 60,000 time-steps. a Configuration B.8; b Configuration C.8; c Configuration D.8

Full size image

The position of the water front is visualized in Fig. 11. For better visibility, the GDL fibers were removed from the image. Six stochastic representations, v1 to v6, were generated. The PTFE was distributed across the same fiber geometry according to configuration A.8. The water front was colored with the through-plane position inside the GDL for better visibility. The water front marches forward in an irregular manner due to the irregular pore structure built by the fibers. Figure 11d shows the saturation curves of the six simulations, v1 to v6. At the beginning, the saturation increases because of the constant mass flow entering the GDL. As soon as at least one droplet leaves the GDL, the increase in the saturation gets lower because now some water also leaves the GDL. In the zoomed region of Fig. 11d, it can be seen that the saturation curves drift away from each other. The change in the slope was determined individually for each of these. This time is defined as the breakthrough point. It can be seen that this situation occurs at slightly different times across the six simulations. On the other hand, the visualizations of the droplets on the rough GDL surface shown in Fig. 9 were taken as snapshots at fixed time after 60,000 time-steps. At this time, at least one droplet occurred on the surface in all simulations.

Fig. 11
figure 11

Water front development in configuration A.8. GDL fibers removed for visibility. Situation of one of six representations after: a 20,000; b 40,000; c 60,000 time steps; saturation curves of six representations v1 to v6

Full size image

The breakthrough point is chosen as a characteristic of a simulation snapshot, and also the number, total volume and total surface of the droplets emerging from the rough surface of the GDL at this time. The breakthrough point is the first point at which the liquid water left the GDL surface. Because the simulations were run with a fixed simulation time, the situation at the end is a snapshot of a dynamic process. The resulting characteristics are therefore related to the breakthrough time. The variations in the breakthrough time, surface and volume of the droplets are illustrated in Fig. 12.

Fig. 12
figure 12

Characteristics of droplets leaving the GDL surface. Statistical variation of six representations of the given configurations; a breakthrough time of the first droplet; b total surface; c total volume of the droplets at the snapshot time

Full size image

The boxplots show an inverse relationship between the breakthrough time and size—total surface as well as total volume—of all droplets leaving the GDL. The diagrams in Fig. 12 represent the statistical variation of six representations of each configuration of the PTFE distribution. The breakthrough time as well as the surface and volume of the droplets cover almost the same range in the case of configurations A.8, B.8, C.8 and E.8. There is a noticeable difference for configurations D.6 and D.8. For D.8, the breakthrough time is lower and the droplets are larger than for the other configurations. The values for D.6 are in the same range as those for A.8, B.8, C.8 and E.8. This leads to the conclusion that a smaller total amount of PTFE can lead to the same transport characteristics of liquid water through the GDL micro-structure if it is located in the proper regions of the GDL. This result is consistent with the experiments of Tavangarrad et al. (2018), who found that liquid water emerging from a hydrophobic layer of porous material does not tend to redistribute very much when it enters a hydrophilic region. Mortazavi and Tajiri (2013) measured contact angles on the surface of Toray GDL. While the conditions of their measurements and simulations by Yu et al. (2018a) and Froning et al. (2019) differ, the resulting contact angles are in a fairly similar range. For this reason, the one-sided inhomogeneous global PTFE distribution was chosen as the best option for the next step. Because the previous simulations were based on fully PTFE-covered fibers, the PTFE distribution of configuration D.8 (with 8% PTFE) is completed with configuration F. Configuration F is the same as D – not re-calculated but exactly the same local distribution—with additional PTFE upon the uppermost GDL layer to create a situation close to previous simulations with regard to contact angles (Yu et al. 2018a; Froning et al. 2019).

On the other hand, it is known that some other characteristics of the GDL can be relevant for the water transport. Andersson et al. (2018a), Andersson et al. (2018b) and, in turn, Malhotra and Gosh (2018) demonstrated the relevance of the contact angle of the droplet on the rough GDL surface for the efficiency of water removal in the cathode channel of a fuel cell. It is apparent in Fig. 13a that not much of the PTFE is located at the top fiber layer of the GDL for configuration D.8. It is also obvious that the droplets (in blue) emerging from the GDL have a very flat shape in this case. The contact angles are far from those proposed by Yu et al. (2018a) and Froning et al. (2019).

The impact of the PTFE of the last fiber layer on liquid water transport is shown in Fig. 13. The simulations were run on a micro-structure with PTFE configuration D.8, the one-sided inhomogeneous PTFE distribution with 8% PTFE inside the GDL. Additional PTFE was added to the top fiber layer—in this way, the results in Fig. 13a–c are related to the schematic sketches in Fig. 4a–c. Compared to Fig. 10c, the bottom section of the GDL is identical but the PTFE added to the top fiber layer is visualized in red.

Fig. 13
figure 13

Additional PTFE (in red) at the last fiber layer according to Fig. 6; a none, configuration D.8; b at the last image layer; c around the fibers of the top layer, configuration F.8

Full size image

The simulations were run on the same micro-structure and local and global PTFE distribution to avoid any influence from statistical variations in any of the three stochastic approaches. Additional PTFE was added to gain insight into its relationship to the characteristics of the GDL surface from a macroscopic viewpoint. In step b)—mode F2 in Fig. 4b, PTFE added to the top image layer—62,053 PTFE voxels were added in the \(512 \times 512\) image layer, which is an increase of 2.3%, related to the PTFE distributed across the entire GDL volume, which is depicted in Fig. 13a. The droplets in Fig. 13a, b look very similar. Hence, the influence of the top image layer seems to be very low. From the viewpoint of the liquid water flowing through the GDL, the additional PTFE was added behind the fibers. The situation changes when three sides of the fibers were covered: mode F3 in Fig. 4c, results in Fig. 13c. 113,295 pixels were added to the top fiber layer (six image layers), which is an increase of 6.4% relating to the PTFE across the entire GDL volume in a). However, the small difference in the total amount of PTFE in the right position changes the shape of the droplets at the GDL surface dramatically. The macroscopic contact angle also changes with the shape of the droplet. The contact angles of droplets No. 1 and 2 in Fig. 13c were calculated using the SPPF method.

Both droplets were analyzed under five viewing angles. A vertical post-processing plane was placed through the center of the droplet at angles of 0\({}^\circ\), 30\({}^\circ\), 45\({}^\circ\), 60\({}^\circ\) and 90\({}^\circ\) to the xy-plane. Every 2D cut was evaluated with the SPPF method, resulting in ten contact angles for each droplet. The values are summarized in Table 4. As in our previous work (Yu et al. 2018a; Froning et al. 2019), the contact angles show statistical variation. The contact angles of droplets No. 1 and 2 agree with each other and also with the values published earlier. They are also on the same order of magnitude as the contact angles measured by Planes et al. (2018). According to Andersson et al. (2018a, 2018b), the contact angles have a strong impact on the droplet detachment in the air channels of the flow field.

Table 4 Contact angles of droplets in Fig. 13c)
Full size table

5 Conclusion

Liquid water transport in the GDL was simulated with respect to three stochastic models describing the positions where the PTFE is deposited at the fibers of the micro-structure. Some approaches, namely the parameters of the local PTFE distribution model and the parameters of the SPPF method for post-processing, depend on the resolution of the lattice. The local PTFE distribution mimics the fiber crossings as favored positions. Globally, the homogeneous and inhomogeneous approaches of layer-wise PTFE content were investigated. All configurations of the global PTFE distribution show a large statistical variance and overlap each other—except for the configuration where the PTFE was concentrated in the bottom half of the GDL. From this viewpoint, the PTFE is most effective in the upstream half of the micro-structure. Special attention was drawn to the last fiber layer. It was shown that the PTFE covering the last fiber layer was able to change the contact angle of the droplet, leaving the rough surface of the GDL. It was also found that PTFE has the most prominent impact on liquid water transport when it is located in the upstream region of the GDL. To ensure large contact angles at the rough GDL surface, it is necessary to cover the topmost fiber layer with PTFE.