Steady-State Relative Permeability Measurements of Tight and Shale Rocks Considering Capillary End Effect

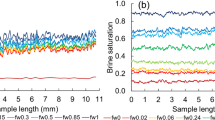
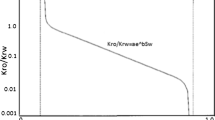
Abstract

Relative permeability (k_r) data are the key factors for describing the behaviour of the multi-phase flow in porous media. During the k_r measurements of low-permeability rocks, high capillary pressure can cause a significant liquid hold-up at the core outlet. This liquid hold-up, which is known as capillary end effect (CEE), is the main difficulty for laboratory measurements of relative permeability (k_r) for tight and shale rocks. In this paper, a novel method is proposed to correct the CEE during the steady-state relative permeability (SS-k_r) measurements. The integrity of the proposed method is evaluated by a set of artificially generated data and the experimental SS-k_r data of an Eagle Ford shale sample. It is shown that accurate k_r data can be obtained using the proposed technique. This technique can be used to estimate reliable k_r data without any saturation profile measurement equipment, such as CT scan or MRI.

Appendix 1

Gupta and Maloney (2016) proposed the intercept technique to correct CEE during relative permeability measurements. The intercept method was proposed to correct CEE errors from both pressure and saturation measurements for each LGR. In this technique, several measurements of rate versus pressure drop are required at the same LGR. The obtained trends in pressure drop versus rate and saturation versus rate will be used to correct the data for each single LGR. To correct the pressure data, one can start with Darcy’s equation as follows

$$ q_{t } \left( {1 - F} \right) = \frac{{ - Kk_{\text{rw}} A}}{{\mu_{\text{w}} L}}(\Delta P_{\text{theoritical without CEE}} ) $$

(A-1)

where $\Delta P_{\text{theoritical without CEE}}$ is the pressure drop across the core without any capillary contribution to the pressure drop. $\Delta P_{\text{theoritical without CEE}}$ can be expressed as the difference between the experimental pressure drop across the core $\Delta P_{\text{Exp}}$ and the pressure drop resulting from the $\Delta P_{\text{CEE}}$. Therefore,

$$ q_{t } \left( {1 - {\text{F}}} \right) = \frac{{ - Kk_{\text{rw}} A}}{{\mu_{\text{w}} L}}(\Delta P_{\text{Exp}} - \Delta P_{\text{CEE}} ) $$

(A-2)

Rearranging Eq. A-2 gives

$$ \Delta P_{\text{Exp}} = \left( {\frac{{\mu_{\text{w}} L\left( {1 - F} \right)}}{{Kk_{\text{rw}} A}}} \right)q_{t } + \Delta P_{\text{CEE}} $$

(A-3)

Using the above concept, Gupta and Maloney proposed to obtain $\Delta P_{\text{CEE}}$ from the intercept of the plot of laboratory-measured pressure drop across the core ($\Delta P_{\text{Exp}}$) and the injected total flow rate ($q_{t } ).$

To correct the saturation data, they used the following overall saturation balance equation for a given fractional flow condition:

$$ L S_{\text{w, avg}} = \left( {L + x_{i} } \right)S_{\text{w, true}} + x_{i} S_{\text{w, CEE}} $$

(A-4)

where $x_{i}$ is the length of CEE region, $S_{\text{w, avg}}$ is average water saturation, $S_{\text{w, CEE}}$ is average saturation of CEE region, and $S_{\text{w, true}}$ is actual water saturation as shown in Fig. 10.

Fig. 10

Schematic of water saturation highlighting the average water saturation ($S_{\text{w, avg}}$), average saturation of CEE region ($S_{\text{w, CEE}}$) and asymptotic water saturation ($S_{\text{w, true}}$) presented by Gupta and Maloney (2016)

They defined CEE length factor as $\beta = \frac{{x_{i} }}{L}$ and proposed the following equation as a reliable concept to correct the saturations.

$$ \beta = \frac{{\Delta P_{\text{CEE}} }}{{\Delta P_{\text{Exp}} - \Delta P_{\text{CEE}} }} $$

(A-5)

Rearranging Equation A-4 and using Equation A-5 gives the expression

$$ \frac{1}{{\left( {1 - \beta } \right)}} S_{\text{w, avg}} = S_{\text{w, CEE}} \frac{\beta }{{\left( {1 - \beta } \right)}} + S_{\text{w,true}} $$

(A-6)

Based on Equation A-6, CEE-corrected saturation (i.e. $S_{\text{w, true}}$) is the intercept of the plot of ($\frac{1}{{\left( {1 - \beta } \right)}} S_{\text{w, avg}} )$ and ($\frac{\beta }{{\left( {1 - \beta } \right)}}$).